粉尘颗粒大小不同,其物理、化学性质有很大差异,不但对人和环境的危害不同,同时对除尘器的除尘机制和性能也有很大影响,是粉尘的基本特性之一。
如果粒子是大小均匀的球体,则可用其直径作为粒子大小的代表性尺寸,并称为粒径。但在实际上,不仅粒子的大小不同,而且形状也各种各样,则需要按照一定的方法确定一个表示粒子大小的最佳的代表性尺寸,作为粒子的粒径。
一般是将粒径分为代表单个粒子大小的单一粒径和代表由各种不同大小的粒子组成的粒子群的平均粒径。粒径的单位一般以微米(μm)表示。
粒径的测定和定义方法不同,所得粒径值也不同。下面介绍几种常见的方法。
(一)单一粒径
单一粒径的测定方法归纳起来有三种形式:投影径、几何当量径和物理当量径。
1.投影径
投影径是利用显微镜观测颗粒时所采用的粒径,可以采用以下几种粒径的定义方法:
(1)定向直径dF,是菲雷特(Feret)于1931年提出的,因此也称为菲雷特(Feret)直径,为各粒子在平面投影图上于同一方向上的最大投影长度。如图4.1(a)所示。
(2)定向面积等分径dM,也称为马丁直径,是马丁(Martin)1924年提出来的。为各粒子在平面投影图上,按同一方向将粒子投影面积分割成二等分的直线的长度,如图4.1(b)所示;
(3)圆等直径dH,也称为黑乌德(Heywood)直径,为与粒子投影面积相等的圆的直径,如图4.1(c)所示。
一般情况下,对于同一粒子有dF﹥dH﹥dM。
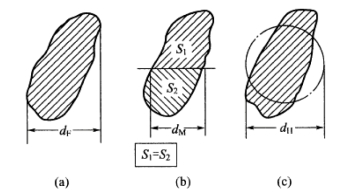
图4.1 用显微镜观测颗粒直径的三种方法
2.几何当量径
取与粒子的某一几何量(面积、体积)相同的球形颗粒的直径为其几何当量径,如球等直径(dr)即与被测粒子体积相等的球的直径。
3.物理当量径(https://www.xing528.com)
取与粒子的某一物理量相同的球形颗粒的直径为粒子的物理当量径,如:
(1)斯托克斯直径(dp),为在同一流体中与被测粒子的密度相同,沉降速度相同的球的直径。当雷诺数Rep﹤1时,按斯托克斯(Stokes)定律得斯托克斯直径的定义式:

式中 μ——流体的黏度,Pa·s;
ρp——粒子的密度,kg/m3;
ρ—流体的密度,kg/m3;
us——粒子在流体中的沉降速度,m/s。
(2)空气动力学直径da,与被测粒子在空气中的沉降速度相同,密度为1g/cm3的球的直径。
斯托克斯直径和空气动力学直径是除尘技术中应用最多的两种直径,原因在于它们与粒子在流体中运动的动力学特性密切相关。
(二)平均粒径
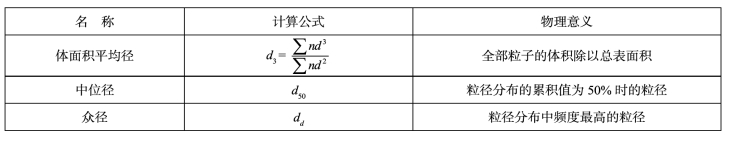
确定一个由粒径大小不同的粒子组成的粒子群的平均粒径时,需预先求出各个粒子的单一粒径,然后求出平均粒径。表4.1中列出了几种平均粒径的计算方法和物理意义。表中的d表示任一颗粒的单一径粒,n为相应的粒子个数。实际工程计算中应根据除尘的任务和要求,粉尘的物理、化学性质等情况,选择最为恰当的粒径的计算方法。
表4.1 几种平均粒径的计算公式和物理意义

续表
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




