高斯扩散公式参数确定-大气污染治理技术

高斯扩散公式的应用效果依赖于公式中的各个参数的准确程度，尤其是扩散参数σy、σz及烟流抬升高度Δh的估算。其中，平均风速u取多年观测的常规气象数据；源强q可以计算或测定，而σy、σz及Δh与气象条件和地面状况密切相关。

（一）扩散参数σy、σz的估算

扩散参数σy、σz是表示扩散范围及速率大小的特征量，也即正态分布函数的标准差。为了能较符合实际地确定这些扩散参数，许多研究工作致力于把浓度场和气象条件结合起来，提出了各种符合实验条件的扩散参数估计方法。其中应用较多的由是帕斯奎尔（Pasquill）和吉福特（Gifford）提出的扩散参数估算方法，也称为P-G扩散曲线，如图3.14所示。由图可见，只要利用当地常规气象观测资料，查取帕斯奎尔大气稳定度等级，即可确定扩散参数。扩散参数σ具有如下规律：①σ随着离源距离增加而增大；②不稳定大气状态时的σ值大于稳定大气状态，因此大气湍流运动愈强，σ值愈大；③以上两种条件相同时，粗糙地面上的σ值大于平坦地面。

由于利用常规气象资料便能确定帕斯奎尔大气稳定度，因此P-G扩散曲线简便实用。但是，P-G扩散曲线是利用观测资料统计结合理论分析得到的，其应用具有一定的经验性和局限性。σy是利用风向脉动资料和有限的扩散观测资料做出的推测估计，σz是在近距离应用了地面源在中性层结时的竖直扩散理论结果，也参照一些扩散试验资料后的推算，而稳定和强不稳定两种情况的数据纯系推测结果。一般来说，P-G扩散曲线较适用于近地源的小尺度扩散和开阔平坦的地形。实践表明，σy的近似估计与实际状况比较符合，但要对地面粗糙度和取样时间进行修正；σz的估计值与温度层结的关系很大，适用于近地源的1km以内的扩散。因此，大气扩散参数的准确定量描述仍是需要深入研究的课题。

估算地面最大浓度值Cmax及其离源的距离xmax时，可先按式（3.17）计算出σ，并图3.14查取对应的x值，此值即为当时大气稳定度下的xmax。然后从图3.14查取与xmax对应的σy值，代如式（3.18）即可求出Cmax值。用该方法计算，在E、F级稳定度下误差较大，在D、C级时误差较小。H越高，误差越小。

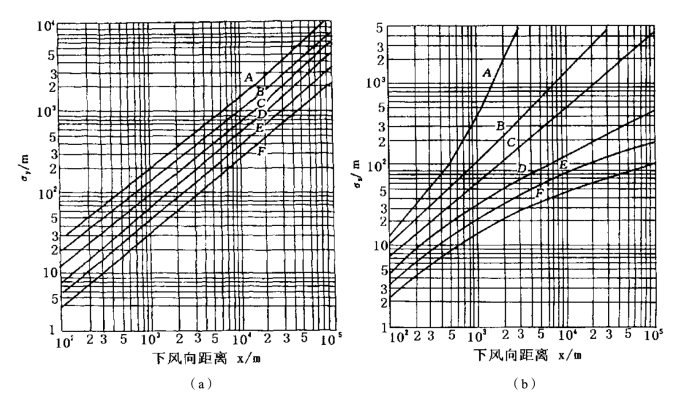
图3.14　P-G扩散曲线（a）σy（b）σ

我国GB3840—91《制定地方大气污染物排放标准的技术方法》采用如下经验公式确定扩散参数σy、σz：

式中，γ1、α1、γ2及α2称为扩散系数。这些系数由实验确定，在一个相当长的x距离内为常数，可从GB3840-91的表中查取。

（二）烟流抬升高度Δh的计算

烟流抬升高度是确定高架源的位置，是准确判断大气污染扩散及估计地面污染浓度的重要参数之一。从烟囱里排出的烟气，通常会继续上升。上升的原因一是热力抬升，即当烟气温度高于周围空气温度时，密度比较小，浮升力的作用而使其上升；二是动力抬升，即离开烟囱的烟气本身具有的动量，促使烟气继续向上运动。在大气湍流和风的作用下，漂移一段距离后逐渐变为水平运动，因此有效源的高度高于烟囱实际高度。

热烟流从烟囱中喷出直至变平是一个连续的逐渐缓变过程一般可分为四个阶段，如图3.15所示。首先是烟气依靠本身的初始动量垂直向上喷射的喷出阶段，该阶段的距离约为几至十几倍烟囱的直径；其次是由于烟气和周围空气之间温差而产生的密度差所形成的浮力而使烟流上升的浮升阶段，上升烟流与水平气流之间的速度差异而产生的小尺度湍涡使得两者混合后的温差不断减小，烟流上升趋势不断减缓，逐渐趋于水平方向；然后是在烟体不断膨胀过程中使得大气湍流作用明显加强，烟体结构瓦解，逐渐失去抬升作用的瓦解阶段；最后是在环境湍流作用下，烟流继续扩散膨胀并随风飘移的变平阶段。

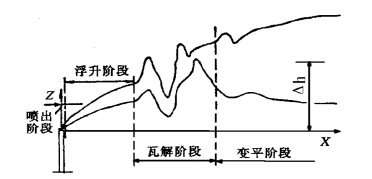
图3.15　烟流抬升过程

从烟流抬升及扩散发展的过程可以看出，显然，浮升力和初始动量是影响烟流抬升的主要因素，但使烟流抬升的发展又受到气象条件和地形状况的制约。主要表现为：①浮升力取决于烟流与环境空气的密度差，即与两者的温差有关；而烟流初始动量取决于烟囱出口的烟流速度，即与烟囱出口的内径有关。一般来讲，增大烟流与周围空气的温差以及提高烟流速度，抬升高度增加。但如果烟流的初始速度过大，促进烟流与空气的混合，反而会减少浮力抬升高度，一般该速度大于出口处附近风速的两倍为宜。②大气的湍流强度愈大，烟与周围空气混合就愈快，烟流的温度和初始动量降低得也愈快，则烟流抬升高度愈低。大气的湍流强度取决于温度层结，而温度层结的影响不是单一的，如不稳定温度层结由于湍流交换活跃能抑制烟流的抬升，但也能促进热力抬升，这取决于大气不稳定程度。③平均风速越大，湍流越强，抬升高度越低。④地面粗糙度大，使近地层大气湍流增强，不利于烟流抬升。

由于烟流抬升受诸多因素的相互影响，因此烟流抬升高度Δh的计算尚无统一的理想的结果。在30多种计算公式中，应用较广适用于中性大气状况的霍兰德（Holland）公式如下：

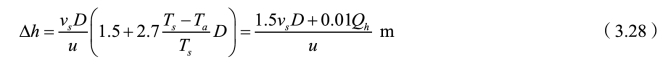
式中　vS——烟流出口速度，m/s；

　　　D——烟囱出口内径，m；

　　　u——烟囱出口的环境平均风速，m/s；(www.xing528.com)

　　　Ts——烟气出口温度，K；

　　　Ta——环境平均气温度，K；

　　　Qh——烟囱的热排放率，kW。

上式计算结果对很强的热源（如大型火电站）比较适中甚至偏高，而对中小型热源（Qh﹤60MW）的估计偏低。当大气处于不稳定或稳定状态时，可在上式计算的基础上分别增加或减少10%～20%。

根据GB/T3840—91《制定地方大气污染物排放标准的技术方法》和GB13223—96《火电厂大气污染物排放标准》，按照烟气的热释放率Qh、烟囱出口烟气温度与环境温度的温差（Ts-Ta）及地面状况，我国分别采用下列抬升计算式。

（1）当Qh≥2100kW并且（Ts-Ta）≥35K时：

式中　n0、n1、n2——地表状况系数，可从GB/T3840—91查取；

　　　V0——标准状态下的烟气排放量，m3/s；

　　　Cp— —标准状态下的烟气平均定压比热，C=1.38kJ/（m3·K）；

　　　Ta——取当地最近5年平均气温值，K；

烟囱出口的环境平均风速u按下式计算：

u0—烟囱所在地近5年平均风速，m/s，测量值；

z0，z—分别为相同基准高度时气象台（站）测风仪位置及烟囱出口高度，m；

m一风廓线幂指数，在中性层结条件下，且地形开阔平坦只有少量地表覆盖物时，n=1/7，其他条件时可从GB/T3840—91查取。

（2）当QH﹤2100kW或（Ts-Ta）﹤35K时：

上式为霍兰德公式（3.28）的两倍。