光子学设计基础第2版-半导体方程

在本书第6章，已经讨论了固体中电子的能量分布。从中知道，该分布是两种因子的乘积：某一给定能量的能级数和一个电子填充该能级的实际概率。

某一给定能量的能级数称为态函数密度（有时称为简并函数）。由于电子被束缚在固体原子晶格内而受到限制，从而使该密度满足一些限制条件（见图Ⅹ.1）。能量E时对态密度的一些认识最终表示在式（6.16）中，即

式中，m^∗_e是“有效”电子质量。

电子是费米子，所以，遵守费米-狄拉克统计学规律。一个电子占据任何给定态的概率可以由附录Ⅶ推导的费米-狄拉克函数确定。因此，实际的密度分布（即单位体积内、具有E和E+dE之间能量的电子数目）由两个函数的乘积确定（见图Ⅹ.1c）：

式中，E_F为费米能量。现在讨论一种半导体材料，在导电带底部的能量为E_C，在价带顶部的能量为E_v。由式（6.25）知道，该材料的费米级位于带隙中间附近的某个位置（即，E_F∝（E_c+E_v）/2，稍后讨论），所以，在绝对温度为零度时，价带中的所有态都是满的，导电带中的所有态都是空的（见图Ⅹ.1a）。费米-狄拉克函数表明，随着温度升高，有一个非零概率，根据T>0时的F（E），导电带中的某些态将被电子填充。

图Ⅹ.1　半导体能级中的密度和填充率

价带中的态不被电子占据的概率是1-F（E），所以也就是这些态被“空穴”占据的概率（见图Ⅹ.1b）。对于导电带，正确的能量E_c代表着该带中被捕获电子的零有效能量，所以，根据式（Ⅹ.1），其能量分布变为

因此，导电带中的总电子数密度为

式中，E_t是该带顶部的能量。这是一个困难积分，然而，借助下列两个简化的合理假设，还是可以运算：

1.只有能带的较低能级有意义，所以E_t完全处于无穷大；

2.E_c值足以超过E_F，使得：

所以，尽管E>E_c，而费米-狄拉克函数分母中的“1”还可以省去。

在上述条件下，积分变成：

价带中的空穴可以完成同样过程，惟一不同的是，必须用1-F（E）替代式（Ⅹ.1a）中的F（E），用m^∗_h代替有效电子质量m^∗_e。为此，利用同样的假设1和2（在负的能量方向），得到价带中空穴的总密度：

为了方便，将式（Ⅹ.2a）和式（Ⅹ.2b）写成下面形式：

式中，n_c和n_p在一定温度下是常数（称为“有效态密度”），由此看到，n和p的乘积是：

这正是所需要的结果，“半导体方程”。该式表明，np与费米能量无关，仅取决于带隙（E_c-E_v）和温度。即使在本征半导体中掺了施主杂质或受主杂质，式（Ⅹ.3）仍是正确的。实际上，在后面情况中出现的现象是，施主原子将电子提供给导电带，并且，根据式（Ⅹ.1a），必须成为均衡状态，其结果是，某些电子落到价带使空穴湮灭，因而，保持乘积np恒定不变。在本征半导体中，空穴数目等于电子数目，所以有：

p=n=n_i

因此(www.xing528.com)

在非本征导体中为

pn=n²_i

但是

p≠n

相反，现在施主和受主的原子密度分别是N_d和N_a，在中性电荷条件下：n+N_a=p+N_d，假设所有的掺杂原子完全离子化，如果N_d和N_a已知，那么，该关系连同pn=n²_i就可以使n和p得以确定。

通常都是下述情况，例如，如果在n类材料中有：

N_d>>N_a，n_i

则

n≈N_d

和

同样，若是p类材料为

N_a>>N_d，n_i

p≈N_a

和

注意到，由于N_d或者N_a>>n_i，所以，在每种情况中，少数载体密度大大低于本征半导体的少数载体密度。

最后，根据式（Ⅹ.2），可以推导出n和p另一个重要结果。根据n和p表示费米能量E_F，取n与p之比的对数，并重新整理，得到：

这就是式（6.26），该式表示，对于p=n的本征半导体材料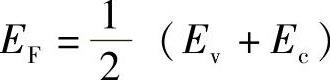，，就是说，在带隙一半处，除非m^∗_e不同于m^∗_h。