光子学设计基础：二次谐波生成（倍频）效果

光波通过非线性光学材料传播时，必须根据麦克斯韦方程正确处理一个基本光波产生的二次谐波。

如果一种绝缘介质的介电常数为ε，磁导率为μ，就可以将麦克斯韦方程写成下面形式：

1.div E=0；

2.div H=0；

3.

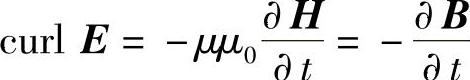
4.

假设，非线性电偏振矢量与施加的电场位于同一方向，则表达式的前两项可以写成下面形式：

P=εχ₁E+ε₀χ₂∣E∣E

因此

D=ε₀E+P=ε₀E+ε₀χ₁E+ε₀χ₂∣E∣E

或者（由于ε=1+χ）

D=εε₀E+ε₀χ₂∣E∣E

将D代入麦克斯韦方程的第4个公式中，有：

对麦克斯韦方程的第3个公式取旋度，并利用数学恒等式：

curl curl E=gra ddiv E-∇²E

（由于div E=0），得到：

再利用式（Ⅷ.1），则有：(www.xing528.com)

假设，现在讨论该公式的一个解，包含由下面形式组成的基波和二次谐波：

E（z，t）=E₁（z）exp[i（ω₁t-k₁z）]+E₂（z）exp[i（2ω₁-k₂z）]

为了确定第一个分量与二次谐波分量之间的关系，可以将此式代入式（Ⅷ.2）中，该关系主要阐述基波如何“产生”二次谐波。显然，这种形式只能是基波分量平方的结果，只有这样才能导致正确的频率。所以，只需讨论以频率2ω₁振荡的项，其他所有的项单独运算。

假设，所有的矢量都是平行的，并与传播方向Oz正交。

现在，依次讨论式（Ⅷ.2）两侧表达式。记住，只关心含2ω₁t的项，替换E（z，t），则右侧项变为

㊀　原书将“4ω²₁”错印为“4ω₁1²”。——译者注

式中，假设对两个分量，μ都是常数，并且对于左侧项有：

对后一个表达式，已经假设：

就是说，在1个二次谐波波长内，∂E₂（z）/∂z明显是常数。令式（Ⅷ.2）左右两端相等，并消去因子（exp（2iω₁t）），得

已知

（因为介电常数和磁导率常数与其作为系数的传播有关，在这种情况中是二次谐波）

由此可以得出结论，消除每侧第一项得到：

或

这就是“发电机”方程，表示E₂（z）的空间增长随E²₁（z）的变化关系。为了确定在非线性晶体中传播距离L后的E₂（z）值，必须对式（Ⅷ.3）进行积分有：

因此，E₂（L）的强度将正比于：

可以看到，这与由（大部分）物理概念推导出的式（9.5）具有相同的形式。详细比较两个公式是有益的，这将作为练习留给读者。