当以直角坐标轴Ox,Oy和Oz为参考轴时,任何偏振光波的两个电场分量都可以写为:
Ex=excos(ωt-kz+δx)
Ey=eycos(ωt-kz+δy) (Ⅳ.1)
令(ωt-kz)=τ上述公式变得比较简单,具体如下:
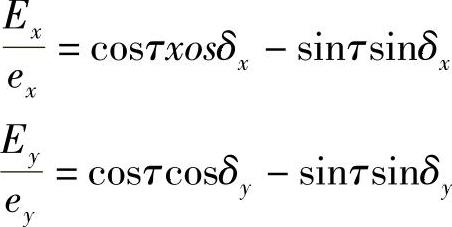
所以
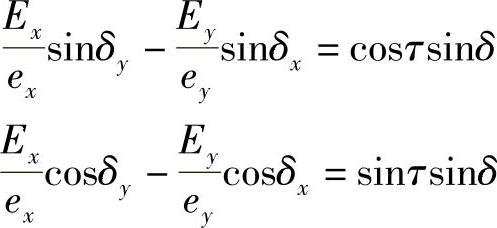
式中,δ=δy-δx,二次方并相加得
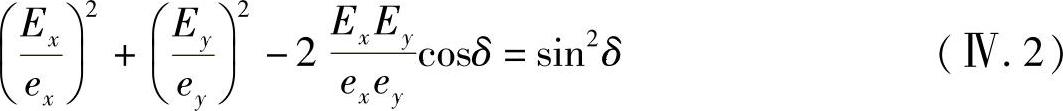
这就是与Ex和Ey相关的偏振椭球(见图Ⅳ.1)。
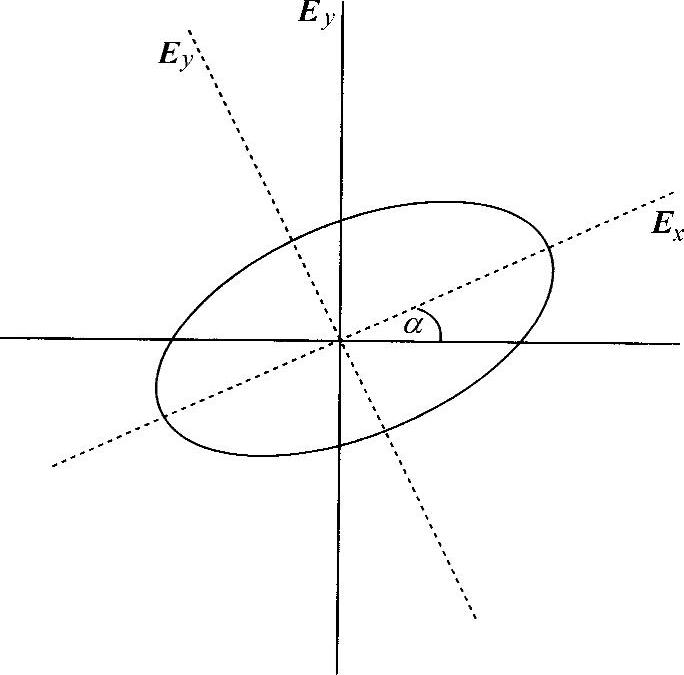
图Ⅳ.1 偏振椭球的坐标系
为确定该椭球的椭圆度和方向,使其轴旋转角度α,就可以将其变成标准形式,即
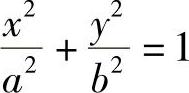
新的场分量E′x和E′y与Ex和Ey的关系为
Ex=E′xcosα-E′ysinα
Ey=E′xsinα+E′ycosα将其代入式(Ⅳ.2)中,有:
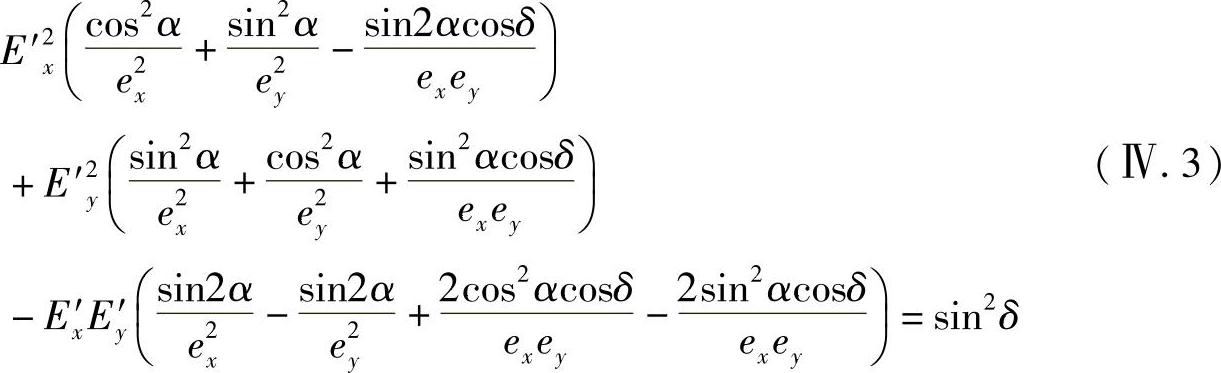
为了将其转换成所需要的标准形式,使交叉乘积项E′xE′y的系数等于零,得到α的值为
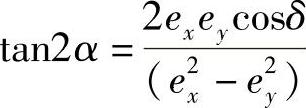
如果确定一个β角,使其:
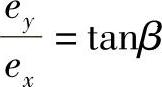
那么(https://www.xing528.com)
tan2α=tan2βcosδ (Ⅳ.4)
带入式(Ⅳ.3),确定一个新的角度χ,有
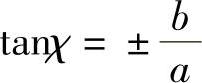
得
sin2χ=-sin2βsinδ(Ⅳ.5)
根据前面的参数ex、ey和δ,可以确定椭球的椭圆度和方位。
现在,取原始轴Ex和Ey,为了测量斯托克斯参数,是随意选取的,有
S0=I(0°,0)+I(90°,0)
S1=I(0°,0)-I(90°,0) (原文将等式右侧的-号错印为+号。——译者注)
S2=I(45°,0)-I(135°,0)
S3=I(45°,π/2)-I(135°,π/2)
正如本书3.8节所述,I(θ,ε)表示,由于插入(或没有)一个四分之一波板(其轴与Ex、Ey平行)而使Ey分量减慢ε角后,入射光通过一个线性偏振器(与Ex夹角为θ)的光强度(见图3.14a)。利用式(Ⅳ.1)给出的Ex和Ey的原始表达式,显然有:
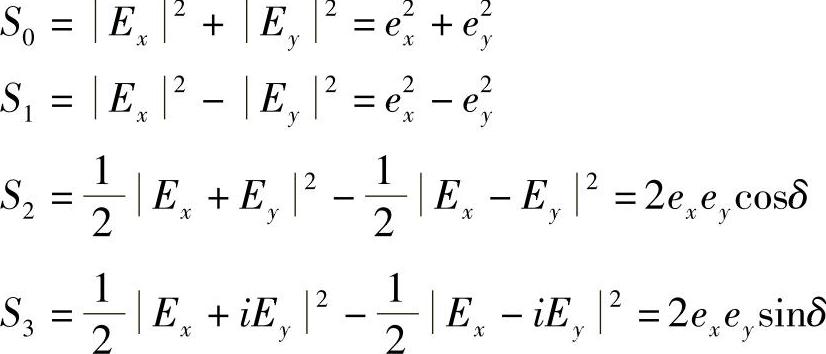
由式(Ⅳ.4)和式(Ⅳ.5),可以得出:
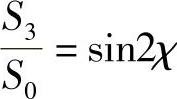
和
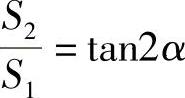
还有
S20=S21+S22+S23
因此,对斯托克斯参量的测量为完整地确定偏振椭球提供了一个迅速和方便的方法。
如果是局部偏振光,则偏振度是:
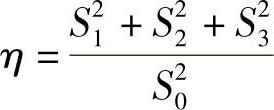
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




