麦克斯韦方程矢量形式解析与光波强度理解

可以用矢量形式表示麦克斯韦方程：

1.divD =ρ（高斯（Gauss）定理）；

2.div B=0（非自由磁极）；

3.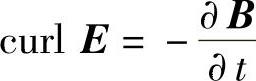（法拉第（Faraday）电磁感应定律+楞次（Lenz）定律）；

4.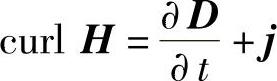（安培（Ampere）电流定理+麦克斯韦位移电流）；式中，ρ为电荷密度；j为电流密度；B=μH和D=εE；div表示散度，curl表示旋度。

在自由空间中：μ=μ₀；ε=ε₀，ρ=0，j=0。所以，上述公式变为

1.div E=0；

2.div H=0；

3.；

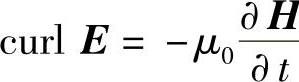4.。

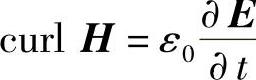对第3个公式再取curl，得到数学恒等式：

curl curl E=grad div E-∇²E

所以，

由于div E=0，因此：

这是波速为下面形式的E的波动方程式：

根据对称性，显然H也有一个类似的解。

E的正弦形式解为(www.xing528.com)

E_x=E₀exp[i（ωt-kz）]

在这种情况下，根据第3个公式，并利用解E=E_xi+E_yj+E_zk（由于E_y=E_z=0及∂E_x/∂y=0），则有：

因此，H只有一个y分量（矢量j）。并且：

H_y=H₀exp[i（ωt-kz）]

作为H_y的对应值。

此外，利用式（I.2）：

式中，Z₀称为该情况下自由空间的电磁阻抗。

相当普遍的为

电磁波中单位体积内存储的能量（根据基本的电磁学原理）为

由式（I.3），有：

U=εE²=μH²

所以，存储在任一场中的能量是一样的。分量E_x和H_y在Oz方向每秒钟通过的单位面积能量为

E和H的矢量积是坡印廷矢量，即

Π=E×H

表示在波传播方向通过单位面积的能量通量。所以，其在一个光波周期内的平均值表示光传播方向单位面积的平均功率，因此等于光波强度（或者辐照度）。