光子学设计基础：第2版详解长短界限区分

已经注意到，“长”和“短”领域的光纤具有完全不同的PMD特性，特别在PMD随长度增大的速率方面更为明显。很清楚，对实际光纤，需要几种判定光纤属于何种范畴的方法。这可以通过“相关长度”（指定为L_c）来定量表示，粗略地讲，就是光在光纤中的偏振态完全没有输入态形式后的长度，主要受偏振扰动所约束。显然，L_c是一个统计实体，必须根据统计学术语严格定义，并且为区分两种光纤提供了非常方便的判断准则。对于一段长度为l的光纤有：

l<L_c　短光纤

l>L_c　长光纤

研究“相关长度”最方便的方式（与许多其他偏振问题一样）是将该过程反映到庞加莱球上。如果用大量等长度（等长度的符号为l_e）的相关长度表示某一给定光纤（即光纤分为大量l_e），那么从统计学观点讲，所有的都将遇到相同的扰动，每一个都具有同样的输入偏振。全部的输出偏振都以图表形式绘制在庞加莱球上（见图10.50）。可以看到，当l_e很小时，输出偏振态都位于该球上（如果在该段长度内光纤非常均匀，显然输出态完全能被确定，并且对所有光纤都是一样的；输出反映在庞加莱球上是一个点）。增大光纤的l_e，则在庞加莱球上的面积增大，直至l_e取某个值，所有可能的输出态均匀地覆盖了该球为止。由于所有输出态可能一样，至此，输出态变得与输入态无关。首次出现的l_e值就是相关长度L_c。

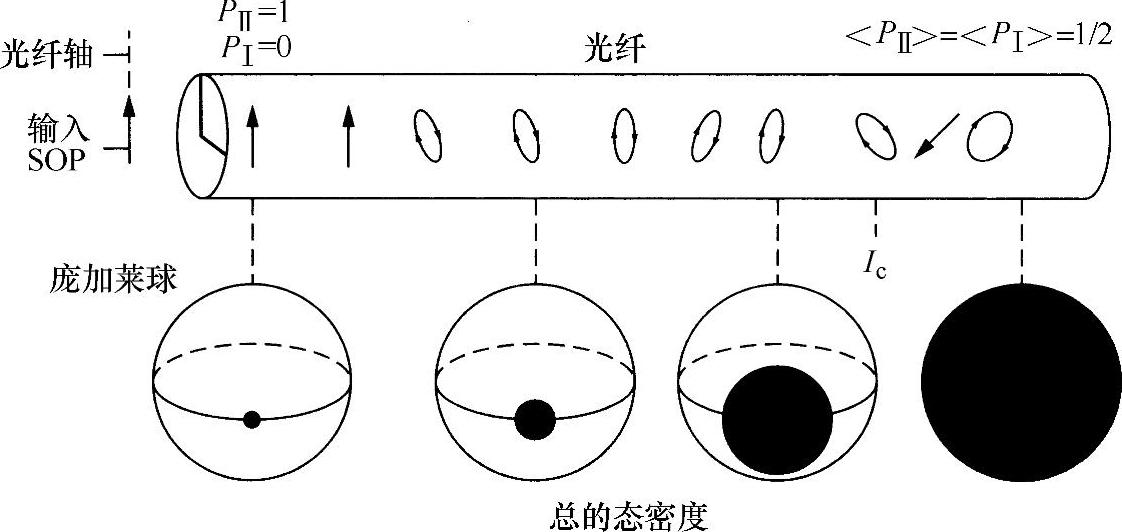
图10.50　长光纤中偏振态的解相关^[6](www.xing528.com)

（资料源自：Academic Press）

L_c定义为，从输入偏振态渗漏到其正交态的能量是总输入能量的0.135（即1/e²）时的光纤长度。

然而，根据前一段给出的定义测量L_c值，并非一件容易的事，因为需要把光纤切割成不同长度的许多段。然而，为了进行满意的测量，可以利用τ的变化与式（10.29b）给出的入射光光学频率的变化等效性。若是短光纤情况，频率变化将造成输出态绕着庞加莱球上的本征矢量旋转；对于长光纤，其作用就是按照统计规律改变所有被连接基元段的τs，因此，就如同移动一段光纤容易受到扰动一样，并遵循同样的统计规律，表现是完全相同的。可以得出结论^[6]：如果频率变化造成输出态在庞加莱球表面均匀地受到扰动，那么该光纤就属于长光纤范畴，反之亦然。

利用琼斯算子对PMD进行比较正规的分析，请参考本书附录Ⅺ。