光子学设计基础：对光路长度的依赖性

10.10.6.1.1　“短”光纤

已经介绍过（见本书3.8节），任何均匀的偏振元件都具有两种偏振本征模，一般是椭圆偏振态，会以不同速度通过元件传播。入射到元件上的任何偏振态都可以分解成这些偏振分量，然后在输出端重新组合，包括与速度差对应的相对相位延迟，以形成输出态。简单地说，该过程的数学操作就是琼斯（Jones）矩阵对输入态的运算，本征模就是矩阵本身的模。

在本书8.7节已经看到，可以由下式确定拍长：

b=λ/Δn

式中，Δn为两种本征模的折射率差；λ为正在传播的光波波长。假设以光脉冲的形式输入，将两个本征模等量分开。若是线性本征模的特殊情况（见图10.49），输入脉冲就被分成一对脉冲，两个本征模各一个脉冲，之间的延迟为τ。如果光纤折射率与波长无关，则有：

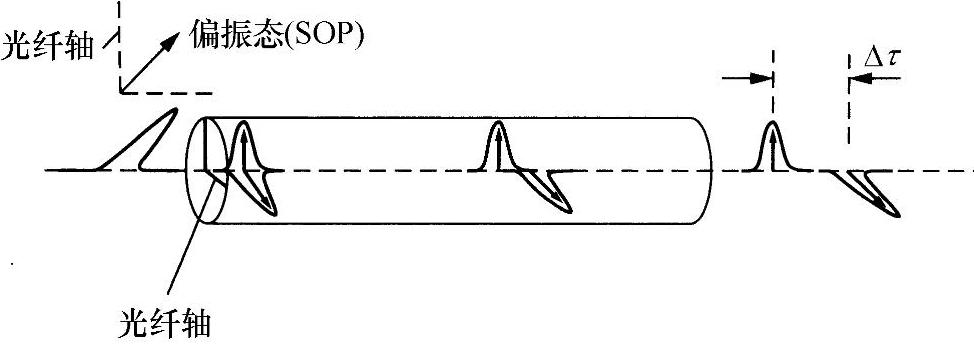
图10.49　短光纤中线性本征模的分离^[6]

（资料源自Academic Press）

τ=L（n₁-n₂）/c₀=LΔn/c₀

式中，L为光纤长度；c₀为光在自由空间的速度；n₁和n₂为两种本征模的折射率。然而，n₁和n₂实际上与波长有关，所以是在脉冲分离中起作用的群速之差。因此，根据式（4.9）有：

c_g=dω/dk

所以

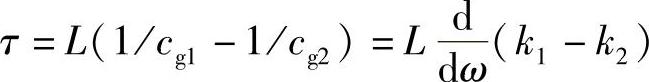
现在

k/ω=n/c₀

因此

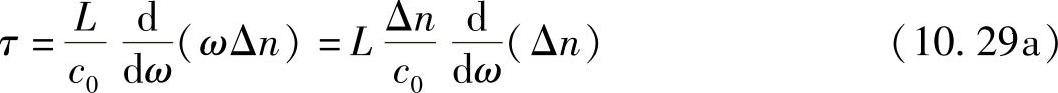
式中，τ是为偏振模色散（Polarization Mode Dispersion，PMD）定义的参数，并认为是一段均匀的光纤。显然，它会随着光纤的长度L线性增大。所以，τ是群速差造成的延迟，并称为差分群延迟（Differential Group Delay，DGD）。

在一个小的频率范围内，频率变化Δω首先造成两个本征模的相对相位有一个滑移。在一段时间τ内，滑移量是Δωτ。所以，无论何时，只要该量是2π的整数倍，就会返回到同样的输出偏振态。如果频率是（在一个小范围内）变化的，那么输出偏振态将以循环的形式变化，循环频率差为

Δω_c=2π/τ （10.29b）

该公式提供了PMD的另一种表示方法，是一个重要的关系式。

然而，在超过几米长度范围内，真正的光纤都不能维持均匀的偏振性质。由于加工缺陷、掺杂浓度的变化，特别在通信光纤的安装过程中，由于弯曲、捆扎及对光纤的横向压力等都会形成不均匀性，因此对“长”光纤进行的PMD分析是完全不同的。

10.10.6.1.2　“长”光纤

对于长度超过10m的已安装光纤，光纤的偏振性质不再是均匀的。在这种情况中，可以将光纤模拟成若干个短光纤的连接，每一段都具有自己的准独立偏振性质。若以这种方式模拟，PMD将不随光纤长度线性增大，理由如下：(www.xing528.com)

每一段光纤的性质都由其偏振本征模及由光纤长度和速度差在它们之间造成的延迟来确定。因此，可以用与庞加莱球上本征模直径相对应的一个矢量表示每一段光纤，其长度等于延迟（等效于庞加莱球绕着本征模直径有一个旋转）。如果这些光纤段无限短且长度相等，那么由于小量旋转是按照矢量方式相加的，所以有限长度光纤的作用等效于这些基元矢量相加。由此产生的最终PMD值就是最终矢量的振幅。

用三维空间（X，Y，Z）中的分量表示每个基元矢量。假设，每个矢量有同样的无限小长度dl，共有N段，所以有：

Ndl=L

式中，L为光纤长度。所以，第n段光纤分量是（X_n，Y_n，Z_n）。其中，n是1到N。

由于每一个分量都彼此独立，并且偏振扰动是沿光纤长度L随机分布的，所以，假设，3N个分量中每一个都是在零周围随机分布（高斯分布形式）的。

通过基元矢量相加产生的矢量振幅的二次方为

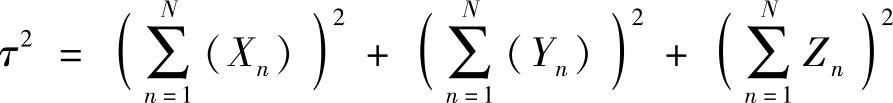
由于分量是独立的，并且每个分量都可能是正或负，由此得出结论：对于一根长光纤，叉积项之和的平均值将为零，即

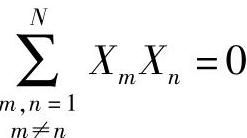
对于Y_mY_n和Z_mZ_n，情况类似。

因此，对长光纤有：

因为是随机分布，将有：

<X²_n>=<Y²_n>=<Z²_n>=α²　（假设）

式中，<>代表平均值。

根据式（10.30）有：

τ²=3Nα²

所以，τ值由下式给出：

式中，τ为最终PMD矢量振幅的中值，定义为PMD的延迟。根据式（10.31）和Ndl=L，可以得到：

延迟随光纤长度L的二次方根增大。