光波导耦合和开关：尽善尽美！

本节需要的主题内容：

i）光学波导（本书第8章）

ii）耦合振荡器（本书第6章）

iii）电光效应（本书第7和9章）

iv）集成光学（本书第8章）

v）马赫-曾德尔干涉仪（本书第2章）

vi）渐逝波（本书第2章）

在光纤通信及其他应用领域，有许多理由可以非常方便地，有时候是必须地，将光从一种波导耦合到另一种波导，可以在平面波导或柱面波导之间耦合。例如，波分复用系统一个重要的问题就是将来自不同光源的光耦合到一根传输光纤中，每个光源被单独调制。当它们从非常远的一端出射时，需要“解复用”（即重新将它们完全分离）。另一个例子是，在上两节讨论的装置中，对光学放大器或激光器的光学泵浦源提出了两个问题。实际上，这是第二个问题（即如何将泵浦光耦合到光纤中，以便与信号共轴传播）。

光纤耦合器是一个具有特殊结构的例子，可以在任意两个波导之间进行耦合。现在，就来讨论这方面的内容。

如果允许两个振荡器相互作用（即激励彼此的振荡），能量将在两者之间周期性传递。对这种现象最简单直接的解释是，两个一样的钟摆在一个共用支架上耦合（见图10.40），耦合后的系统是一个完整的整体，可以用复合术语阐述——有两个振荡本征模。即，它有两种不会随时间变化的振荡状态（假设，没有耗散力，例如空气阻力）：第一种是两个钟摆具有相同的振幅，并同相位振荡，称为模式1，振荡频率为f₁；第二种是具有相同振幅，但反相位振荡，振荡频率为f₂。假设，初始两个钟摆静止不动；之后令一个摆动，当第一个钟摆正在加速时（最大加速度是在摆动的极值位置），在沿支架传输过去的力的作用下，与另一个钟摆相互作用，第二个钟摆开始摆动。当周期性的一个力以谐振频率（同样的钟摆）驱动一个振荡器时，的确以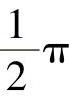的相差摆动，这就是说驱动力的振幅与该振荡器的位移振幅相差1/4周期。原因是该力没有受到振荡器恢复力的抗衡时，即在振荡器摆动的中间点（中性位置），对增大其作用的质点速度最有效。这意味着，力和振荡器是正交的。如果是两个钟摆的情况，一个钟摆的驱动力（最大值位于摆动的极值位置）对另一个钟摆的中间摆动位置会产生最大影响，因此第二个钟摆与第一个钟摆是以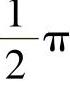的异相进行振荡（图10.40）。由于第一个钟摆的运动而使第二个钟摆的振幅增大，所以第二个钟摆开始对第一个钟摆产生回反应（或者逆反应），再次产生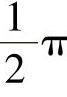的异相，所以与第一个钟摆完全是反相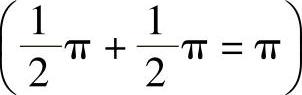。其结果是，第一个钟摆使其摆动振幅减小，而第二个钟摆的振幅增大，直至第一个钟摆静止，第二个钟摆具有最大振幅为止。之后，该过程会反向继续，所以摆动能量会连续地在两个钟摆之间传递，转换频率是f₁-f₂。显然，f₁-f₂取决于两个钟摆之间的耦合强度，耦合越强，f₁-f₂就越高（对于零耦合，每个单独振荡的频率f₁=f₂=f，并且f₁-f₂=0）。

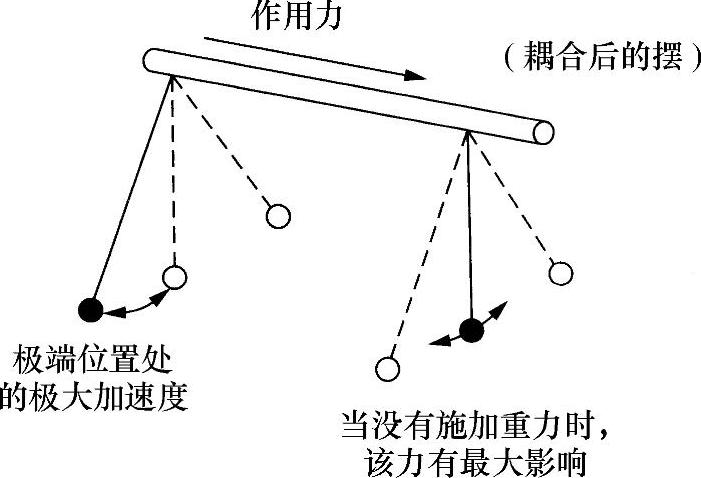
图10.40　耦合振荡器之间的组合关系

现在，将这些思想应用到耦合光波导中。

假设，有两个同样的相距非常近的平行波导，以便使其瞬逝场相重叠（见图10.41）。在这种情况中，如果一束光学波正在其中一个波导中传播，其中部分光会漏射到第二个波导中，两个波导就会发生耦合。耦合的结果是，第一个波导的光学电场作用在第二个波导的原子振子上，从而使它们处于运动之中（古典物理学方法）。如同钟摆一样，将有一个π/2的相对相位。随着光波沿着一对波导传播，第二个波导中的光波强度将增大，并且以反相回到第一个波导上，仍像钟摆一样使其振幅减小。随着传播的继续，光纤能量以某种空间频率（即在一个波导距离范围内）在两个波导之间来回转换，该频率取决于耦合强度。由此可以得出结论：如果耦合强度和距离选择合适，那么在光波传播此段距离后，所有光能量都将从一个波导转换到另一个波导；如果在该点使波导分离，便构成一个有效的波导耦合器，将光波从一个波导耦合到另一个波导中。(www.xing528.com)

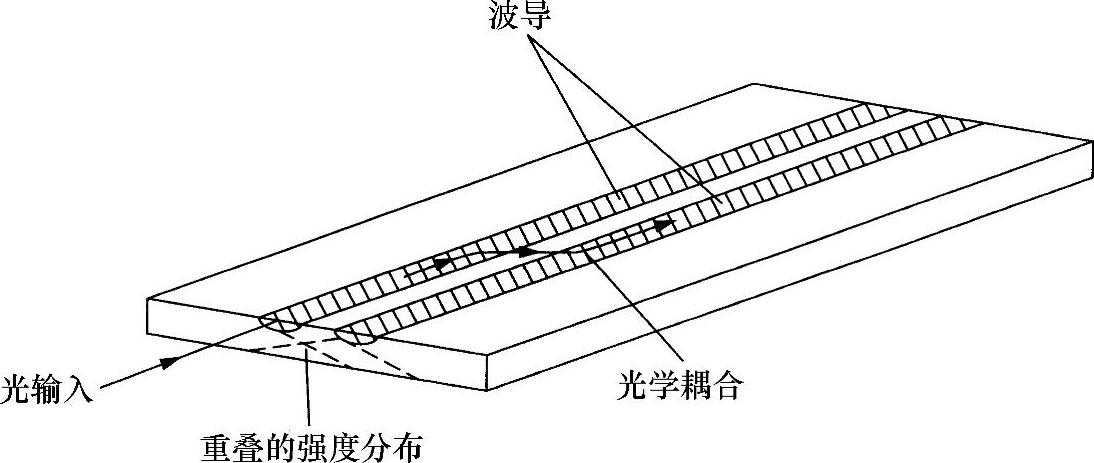
图10.41　耦合光学波导

假设，有两根光纤包裹熔凝在一起，其长度恰好能出现一个完整的耦合（见图10.42）。如果其中一根是通信线路的一部分，并且其中的一段掺杂了铒元素，那么就可以利用另一根光纤耦合，如1480nm半导体激光器发出的泵浦光。

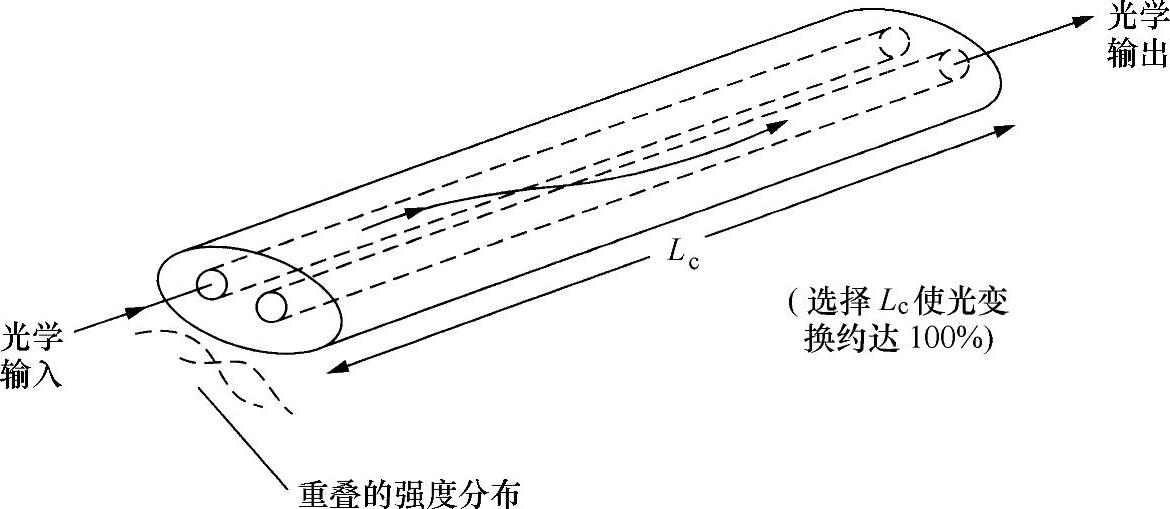
图10.42　熔凝包裹在一起的光纤耦合器

可以更巧妙地利用这种思想。现在讨论图10.43所示的集成光学结构。在这种情况中，两个耦合平面波导加工在LiNbO₃电光材料中。该方案设计有电极，可以将外部电场施加在波导上，施加电压的作用是改变波导材料的折射率，从而改变波导中光信号的传播常数，也就改变了系统本征模的频率（即改变钟摆模拟系统中的f₁和f₂）。可以看出，是用电压控制波导间发生耦合的空间频率f₁-f₂，所以，当电压为零时（例如），所有光束都从波导1中出射。电压为V时，在相同的传播距离内，所有光束都从波导2中出射，从而得到了一个光子开关。光可以在波导之间以GHz的速率进行开关（仅受限于材料对电压的响应速度，即对电光效应的响应速度）。显然，对于通信和许多其他应用，这是一种非常有用的器件。

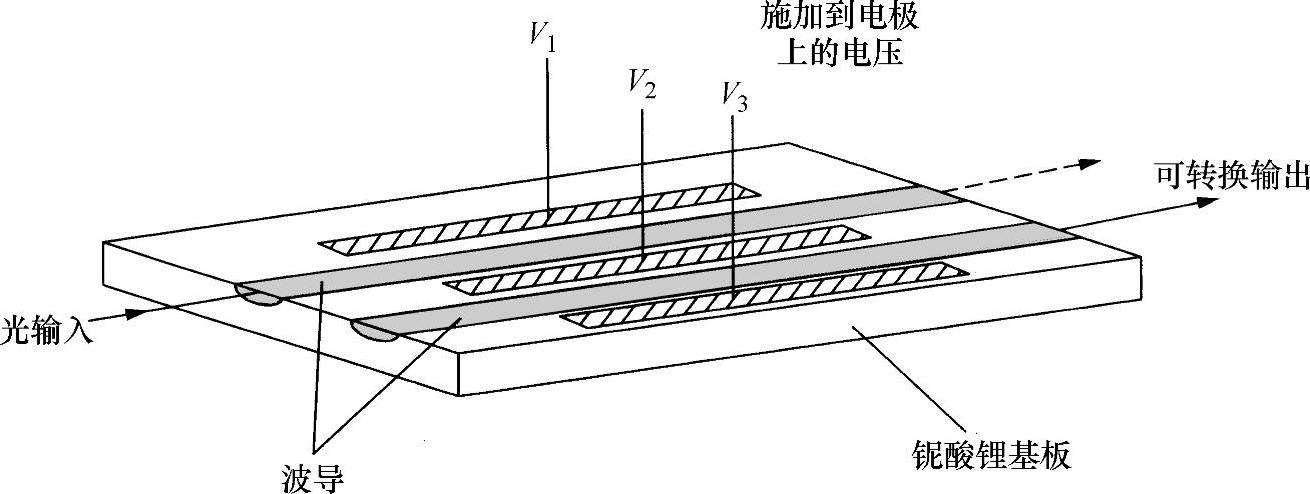
图10.43　一种可以开关的平面光学耦合器

至此，已经讨论的装置都是采用相同的波导，非对称波导也可以耦合，并具有非常有意义的性质。对这些耦合效应的完整分析相当复杂，包括对二阶微分耦合模方程求解。显然，对任何以此效应为基础设计器件（或装置）的设计师来说，对该分析的完整理解是必要的，并且可以从其他文章中（如参考文献[5]）得到这方面的内容。

图10.44a所示为另一类型的电光集成光学波导开关。这是本书2.9节讨论的马赫-曾德尔干涉仪中使用波导的例子。线性偏振光从前端入射到单模波导中，并在第一个Y结处分成两个相等的分量。两个分量分别在两条光路中传播，在第二个Y结处重新汇合。显然，如果两条光路完全精确地相等，并保持一样的偏振，那么两个分量在第二个Y结处将是同相，因此在输出端会得到一个等于原始输入强度的光强度。然而，如果在电光材料中马赫-曾德尔干涉仪一支光路中施加一个电压，使该光路中光的相位改变π，那么两束光重新组合时将是反相的，集成光学模块的输出就是零。因此，电压的作用相当于最大与零输出之间的开关，通过改变施加的电压，可以获得各种必要值。

甚至有希望利用一束光为开关提供所需的电场，通过光电效应实现用光开启和光关闭的目的。此外，如果光的开启和关闭是源自波导输出（见图10.44b），那么当输入高于某一电平时，该开关保持在“on”（开）的状态，低于该电平则转向“off”（关）。因而，形成一个可以区分不同光能量水平的双态开关，这是一个“光逻辑门”的例子，可以应用于光学信号处理或以更先进的形式应用在光计算中。

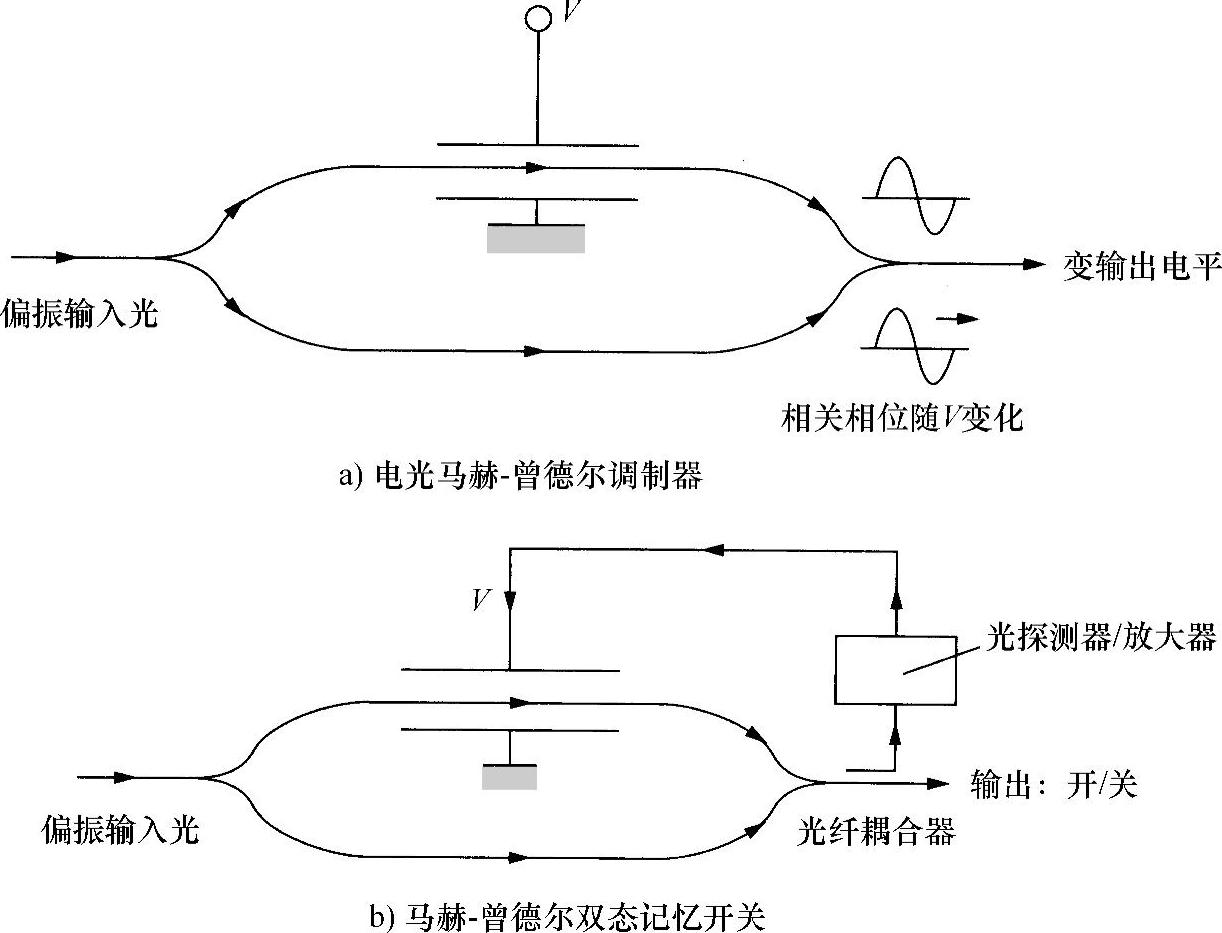
图10.44　电光马赫-曾德尔光学开关