光子学设计基础：超短光脉冲测量

本节需要的主题内容：

i）非线性磁化系数（本书第9章）

ii）二次谐波产生（倍频）（本书第9章）

iii）相关（本书第5章）

iv）光电子探测的响应时间（本书第7章）

非常短（有时也称为“超短”）激光脉冲提高了各种应用领域的技术要求。这类脉冲处于飞秒数量级，由于有很少的探测系统能足够快地响应，所以很难精确地分辨时间。例如在时间分辨光谱领域，需要应用超短激光脉冲来研究快速化学反应的动力学；在高速转换系统中，用来分析半导体内电荷的转换效应，以及具体的一些仪器系统，如激光雷达（即OTDR，激光雷达）、光学计算和存储、高速抽样和示波镜。

为了正确理解所提供的这些窄脉冲数据，必须对脉冲的振幅和相位形状有相当透彻的了解。也就是说，必须及时知道有关其（复杂）形状的一些内容。例如，除非知道脉冲的时空形状，否则不可能根据反应动力学解释超短激光脉冲激励一种化学反应得到的实验结果。如果知道，就可以根据提取的脉冲形状获得该结果，这就是一种称为“反卷积”的过程。

对于宽度小到约10ps的脉冲，利用高速光敏二极管和快速示波器相结合以实现“直接”探测。如果脉冲是重复的，使用抽样示波器，在这种情况中，观察其中一小部分脉冲以从中抽样任一个脉冲，并且在一些连续脉冲中根据扫描通过该脉冲形状的抽样时间就可以得到完整的脉冲形状。对于脉冲宽度在0.5～10ps之间的脉冲，可以使用一种称为“条纹相机”的装置。如此，使光脉冲入射到光阴极管上，与光倍增管一样，产生光电子，电子被加速射向阳极（仍像光电倍增管一样）。但是，在一个很强的横向电场作用下，它同时快速偏向一侧，然后落在一个磷光屏上，结果在屏上出现一根条纹。其强度变化显示原始脉冲的时间演变。条纹相机是一种非常精密和昂贵的装置（见图10.27）。

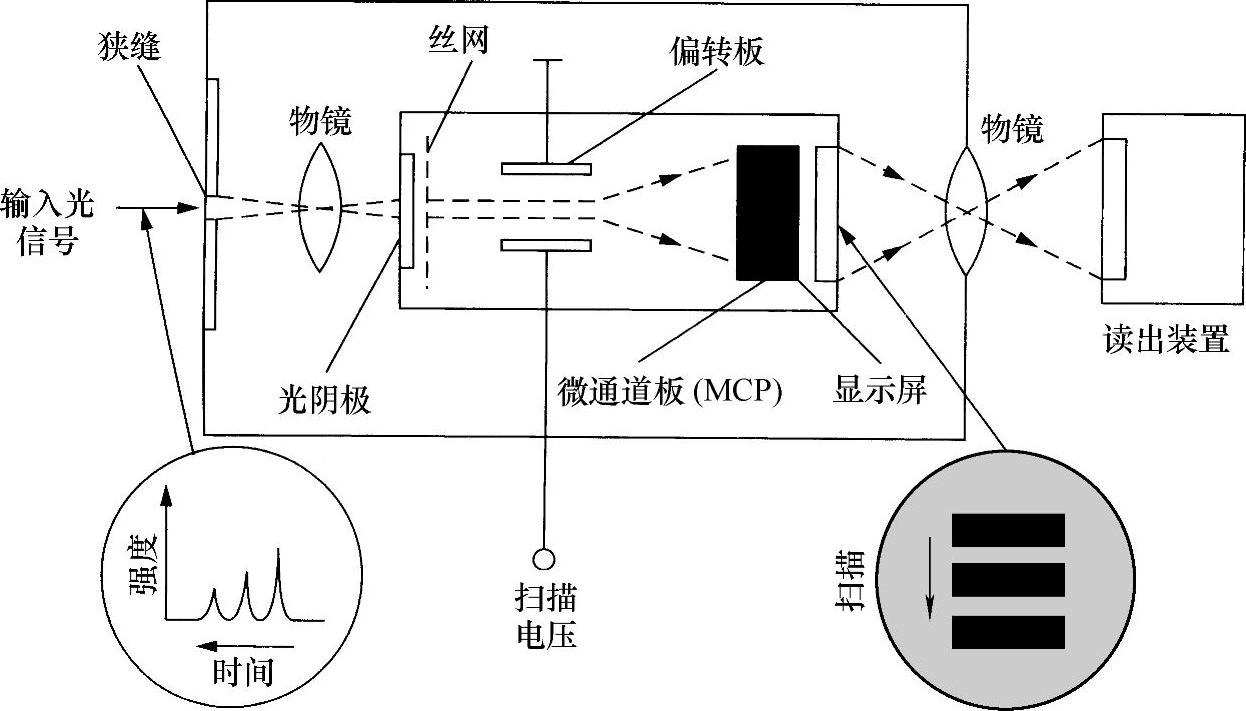
图10.27　条纹相机的示意图

比条纹相机更廉价，同时使时间分辨率降至几十个飞秒的一种装置就是自相关器。

自相关器（autocorrelator）的设计原理源自前面讨论的两种思想：自相关（不出所料）和二次谐波产生。图10.28a给出了用于测量脉冲宽度的自相关器的作用原理。分束镜将被分析的（准单色）光脉冲分成两个同样的光路，每只光路都传播到一个“屋脊”棱镜形式的反射镜上（屋脊棱镜是一种简单棱镜，可以实现如图所示的反射。其功能是保证反射后的光完全与入射光平行传播，简单的几何形状（见图10.28b）表明，即使该棱镜绕其轴有小的转动也是如此，不会影响上述性质。其优点是，不必进行精确的角度对准，就像该情况一样，需要改变反射镜位置时，特别有用）。如图10.28所示，一个棱镜的位置是变化的，所以在两个一样的半脉冲中会插入一个变化的时间延迟。这是一种非常方便的方法，用以控制超短脉冲宽度以及时间延迟。例如，5μm的位置变化是完全可以实现的，对应约33fs的延迟。

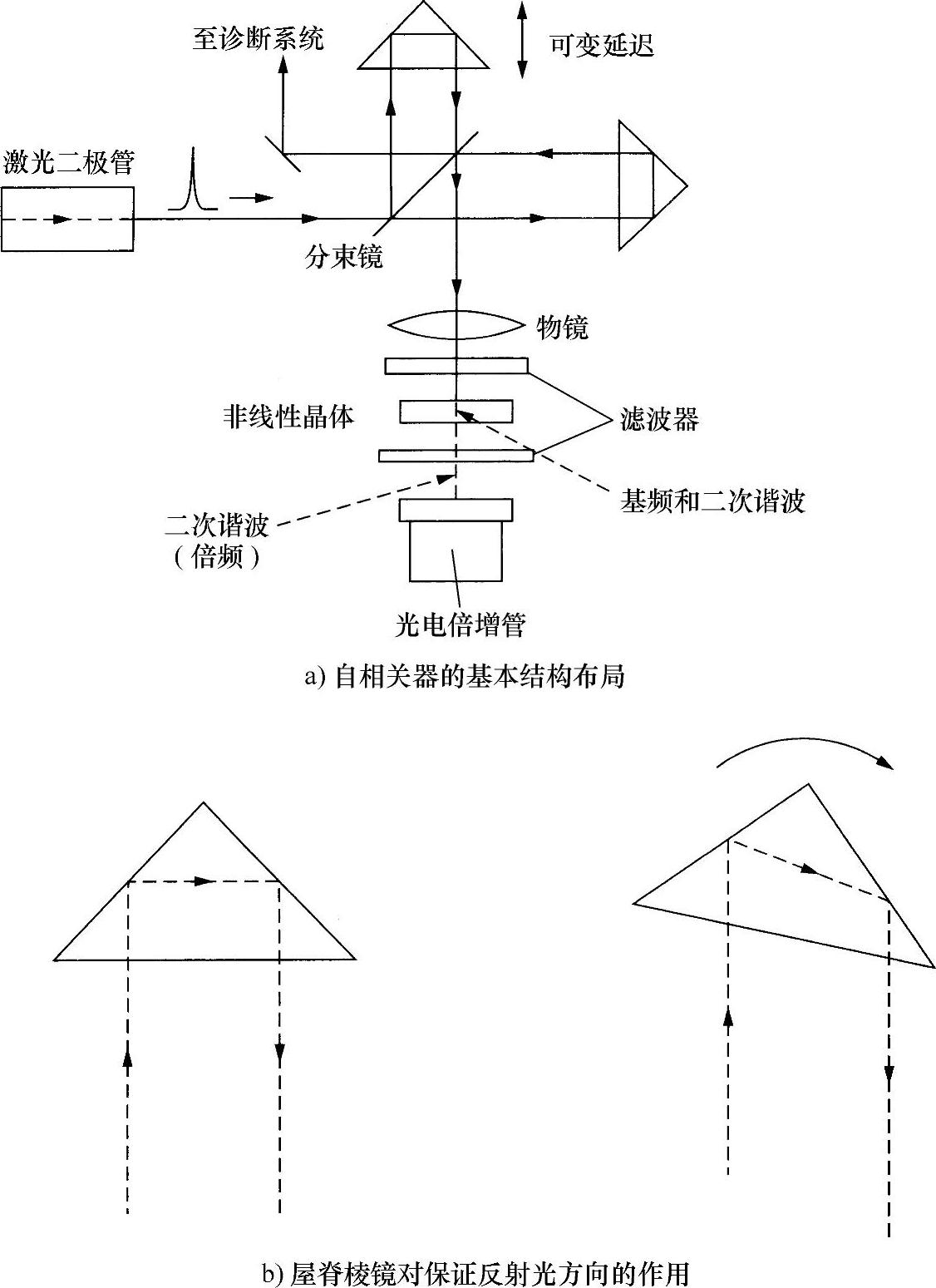
图10.28　光学倍频自相关器

在给定时滞后，两个半脉冲重新组合（使到此位置的整个系统基本上形成一个麦克尔逊干涉仪），由此产生的共线光束经过一个透镜和一个光学滤光片入射到非线性晶体中。该透镜保证光束准确地聚焦在晶体中。滤光片的作用是排除所有不需要存在的光（例如，如果脉冲源自固态激光器，那么在初始光束中可能有二次谐波产生——显然应当排除）。

当光束相对于晶轴以合适角度和正确的偏振方向传播到倍频晶体时（见本书9.4节），将产生光学基频的二次谐波。二次谐波的程度取决于两个半脉冲间的相对延迟。粗略地说（后面有正确分析），可以通过下面方式理解：如果分束前，初始脉冲恰好没有延迟，则二次谐波的程度正比于其强度的二次方。也就是说，正比于I²（见本书式（9.5））；若延迟大于脉冲宽度，则最大强度是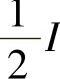I，所以二次谐波量正比于（原文错印为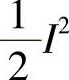。——译者注）。因此，从I²到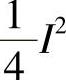范围内达到产生二次谐波水平必需的延迟等于脉宽。该晶体产生的二次谐波分量将通过一个阻挡基频成分的滤光片传播到光电倍增管（Photomutiplier，PMT）。与通常情况一样，如果生成的二次谐波分量具有（与基本光波相比）正交的线性偏振。那么，最后一个滤光片就可以是简单的线性偏振片（一个尼科尔（Nicol）棱镜或渥拉斯顿棱镜）。显然，这种结构布局是一种相当简单直接地测量脉冲宽度的方法。为了全面分析自相关器的作用，必须关注自相关理论。

假设，将要分析的脉冲表示为随时间变化的强度I（t）。该强度对应着一个电场变化E（t），并且有：

∣E（t）∣²=KI（t）

式中，K为一般常数。注意到，由于E（t）包含有光学振幅和相位两种信息，所以是一个复数量。而强度函数没有包含任何相位信息，因而正在讨论的自相关器不可能重新获得相位（在最实际的应用中，待研究系统仅对强度有所响应（即对光通量响应），所以不属于有严重缺点）。

在自相关器中（见图10.28），脉冲被分成两个相等的分量，每个场振幅是e（t），由此得出：

2∣e（t）∣²=∣E（t）∣²=KI（t）

所以

如果其中一个分量（经过屋脊棱镜后）延迟τ，那么两个分量重新组合后，产生的电场就为(www.xing528.com)

e_T（t）=e（t）+e（t+τ）

由式（9.1）知道，二次谐波分量是由于非线性电偏振的原因，由表达式中的二次方项形成，所以可以表示为

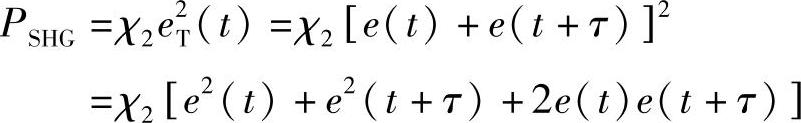
根据本书9.4节的讨论知道，其中每一项都代表一种次谐波振荡的场振幅，所以导出下面形式的次谐波振荡强度：

因此，由式（10.22）得

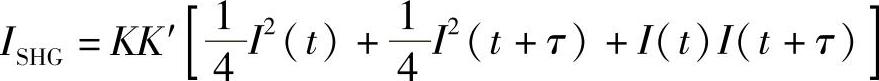
（注意到，最后一项的等值性是依据：两个复数乘积的模等于其模的乘积。）

一个简单的时空延迟不会引起强度的任何变化，由此得

I²（t）=I²（t+τ）

因此

如果作为光电倍增管，则光电探测器不可能在一个脉冲宽度数量级的时间内有所响应。若可以，就使用直接探测，不必采用自相关器。由此得出光电倍增管的输出完全是所有时间范围内对次谐波振荡信号的积分。也就是说，其响应为

该响应由两项组成：一项随时间延迟τ变化，另一项不随时间延迟变化。如果利用后一个“直流”（DC）项（通过实验很容易识别）规化输出，就得到一个规化响应为

该表达式的第二项是I（t）的自相关函数。

很清楚，自相关项从τ=0时为2，变化到τ大于脉冲宽度时为零。在这种情况下，I（t）与I（t+τ）完全无关。总之，结果与本节前面进行的简要讨论相一致。

R′从最大值3变化到最小值1，位于3到1范围内的延迟值τ等于脉冲宽度，可以通过试验确定。R′测量结果的一些例子如图10.29所示，其中含有噪声。然而，任一给定的自相关函数并非对应着惟一的时空轮廓，而是一族形状，所以R′随τ的变化并不会使I（t）的形状惟一被确定。此外，无论实际脉冲多么不对称，自相关函数总是对称的。由图10.29可以清楚地看到这一点，两个脉冲之和总会使τ=0每一侧具有相同形状。

尽管有上述各种约束，自相关器仍然是确定飞秒级脉冲宽度的特别有价值的装置。实际上，在任何情况下，其中的绝大部分都是对称的。一旦选择到合适的晶体，建造自相关器是比较简单和廉价的。碘酸锂（LiIO₃）和铌酸钾（KNbO₃）是常用晶体，并且是不需要快速响应的光电探测器。此外，如果需要，还有更为复杂的（干涉测量）方法重新获得整个形状和相位信息。对于目前要求，这些方法过于复杂，有兴趣的读者可以在参考文献[4]中查阅其详细内容。

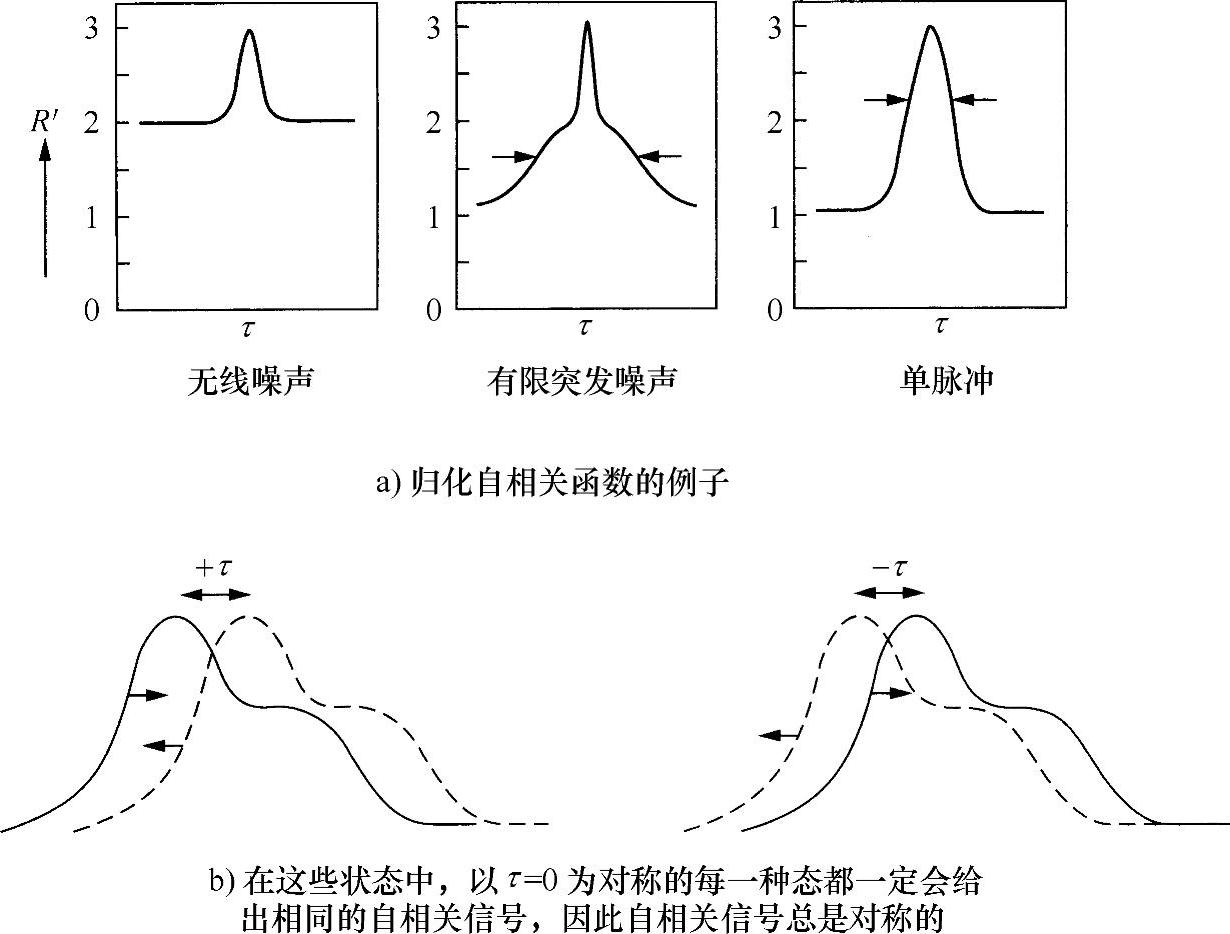
图10.29　自相关信号