光纤陀螺克服缺点，实现角旋转计算

本节需要的主题内容：

i）波相干性（本书第2章）

ii）光前的偏振性（本书第3章）

iii）马赫-曾德尔干涉术（本书第2章）

iv）光学克尔效应（本书第9章）

v）激光调制（本书第7章）

vi）集成光学（本书第8章）

对于导航和自动飞行控制，陀螺仪是非常重要的仪器。以旋转金属盘角动量守恒为基础的普通陀螺仪已经有了快速发展，但是其中还有一些零件需要耗费一定时间（“自旋”时间）才能达到正常工作状态，并易损坏。该装置的安装和维护都较昂贵。

光纤陀螺克服了所有缺点（但必然会有自身的问题）。现在，讨论图10.14所示的结构布局。激光器发出的光通过分束器同时进入光纤环的两端，所以两束光以相反方向在光纤环中传播。当光束在各自一端出射时，再次通过分束器会聚在一起，在一块接收屏上产生干涉。该结构布局可以看作是马赫-曾德尔干涉仪的特定形式。干涉仪的两只分路位于同一段光纤内，但两个信号以相反方向传播。显然，在这些条件下，将在接受屏上形成正弦干涉图。如果两光束强度相等，可视度为100%。

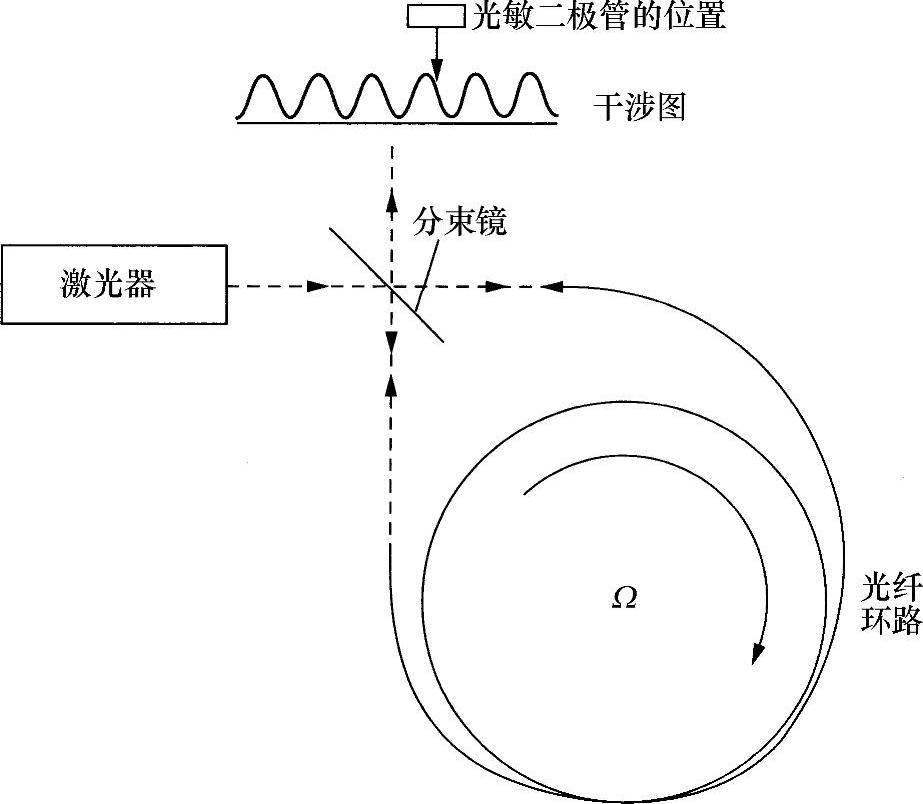
图10.14　光纤陀螺的基本结构布局

假设，整个系统以角速度Ω顺时针旋转。此时，顺时针方向传播的光束在传播过程中会到达光纤尾端，因此出射前传播得更远。相反，逆时针传播的光束将到达光纤的反向尾端，传播距离相对较短。其结果是，两束光之间有一个相对相移，并且在接收屏上的干涉图中必然存在着相移。（实际上，这是物理学稍微简单化的一种解释，确切解释需要借助于相对论。因为旋转系统是加速系统。对于初级理论，在此给出的解释是正确的。）由此得出结论：利用干涉图的变化可以测量转动Ω。在接收屏一定位置放置一个光敏二极管，就可以记录接收能量随横向位移的线性变化（见图10.14）。此后（1913年），这种相移效应称为萨格奈克（Sagnac）效应。

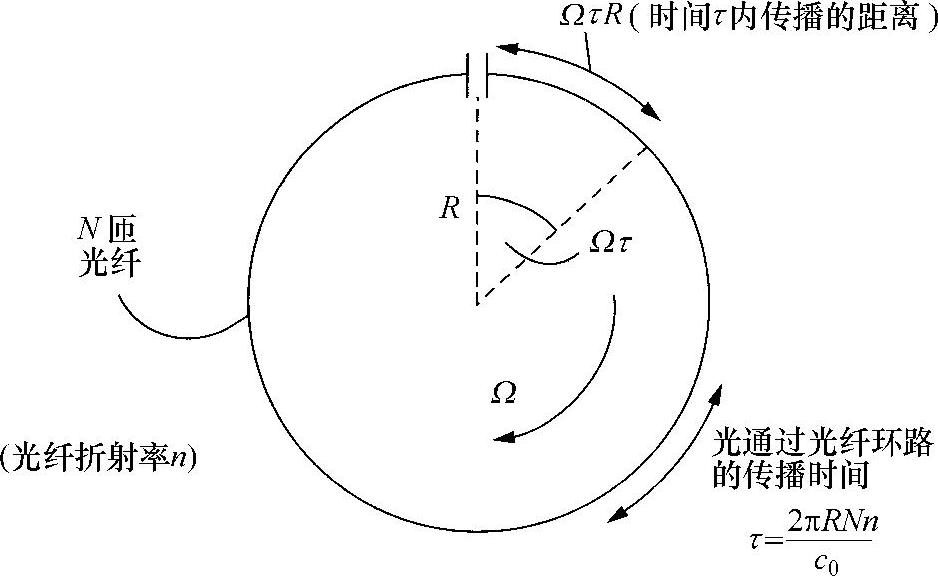
图10.15　陀螺几何特性

很容易计算角旋转造成的相移（见图10.15）。假设，线圈上有N匝光纤，线圈半径为R，若没有旋转，绕线圈传播的时间为

式中，c₀为自由空间中光速；n为光纤材料的折射率。如果线圈绕着通过中心，并垂直于平面的轴线旋转角度Ω，则光束在光纤中传播时，光纤端部已经旋转了一个角度Ωπ，并移动了一段距离ΩπR。两束反向传播光束传播的距离差将是其两倍，即

dl=2ΩπR （10.11）

线圈旋转时，从初始静态架构（“惯性”）观点看，顺时针和反时针传播的光分量将不再以相同的速度传播。必须考虑“菲涅耳”阻力，因此，当某种介质以速度ν在光传播方向移动时，与静态情况相比，光将以下列的速度传播^[2]

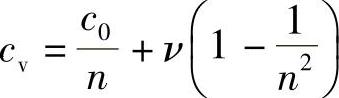
式中，（1-n^-2）称为菲涅耳-斐索阻力系数（这是狭义相对论的直接结果）。对目前情况，围绕线圈的两种速度为

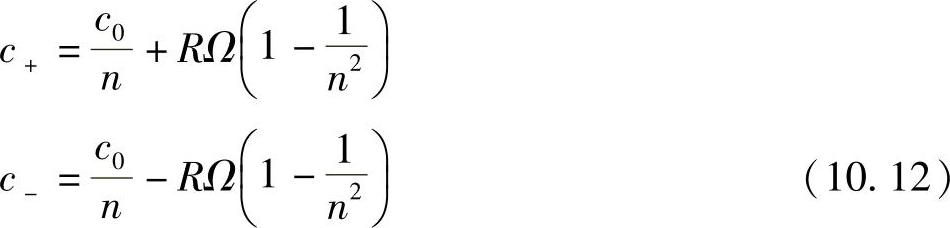
现在，讨论反向传播的两光束到达光纤线圈端部的时间差，有：

和

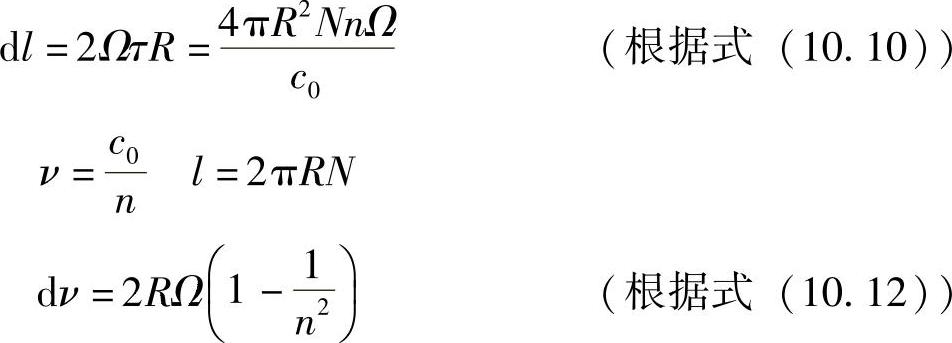
将后面的公式代入式（10.13）中，得

注意到，这与折射率n无关，所以与光纤介质无关（这就是讨论光纤陀螺时，通常使人糊涂的地方）。根据式（10.14），很容易推出光纤旋转时，两个反向传播光束之间的相位差，即

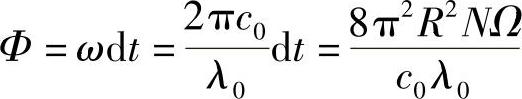
式中，λ₀为自由空间中的波长。也可以写为

或

（原文分母中错印为C₀。——译者注）

式中，A为线圈总的有效面积（由N匝光纤包绕的总面积）；L为光纤的总长度；D为线圈直径。

现在，在式（10.15b）中代入一些数。假设，使用波长为1μm，线圈长度为1km，直径为0.1m。可以得出：(www.xing528.com)

Φ=2.1Ω

若地球转速为15°/h（7.3×10^-5rad/s），所以必须能够测量出1.5×10^-4rad的相移，这可以相当容易地做到。实际上，利用该装置有可能测量约10^-6rad的相移，对应着5×10^-7rad/s的转动速率。

问题是什么呢？首先，只有两束相干光具有相同偏振时才能使条纹的可视度为100%，所以必须使用保持偏振不变的单模光纤，通常是使用线性双折射（高双折射率）光纤。其次，有一个光学克尔效应问题：由于在光学克尔效应中，一束光的电场会起作用，从而改变另一束光的相位。该影响虽小，但寻求测量低旋转速率的相位差也小。利用本书9.6节讨论过的内容，可以计算出这种效应。已经知道，在熔凝石英中，非线性电偏振可以写成下列的近似表达式：

P（E）=χ₁E+χ₃E³ （10.16）

在这种情况下，两个反向传播的光波之和可以得到以下电场：

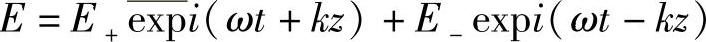
将该值代入式（10.16）得

P（E）=χ₁E+P_N++P_N-

式中

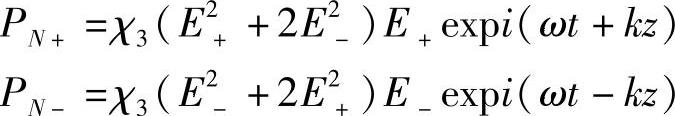
折射率由下式给出：

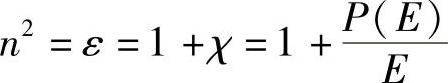
因此，对顺时针（+）传播光束，有：

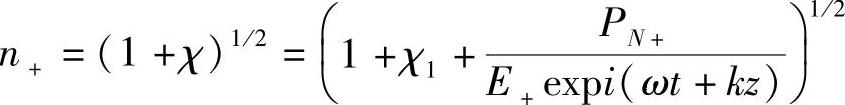
或者，利用二项式定理有：

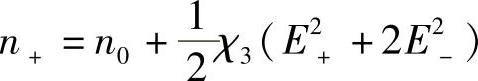
同样

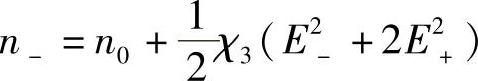
由此得出结论：每个方向的非线性（由光学克尔效应感应产生的）相位变化为

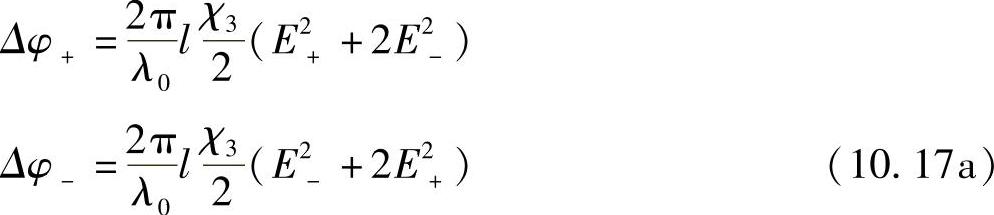
（原文此处的公式与本书10.7节中的一个公式编号重复，将此处公式编号改为式（10.17a）。——译者注）

显然，除非E²₊=E²_-，否则这两个值是不等的，其差为

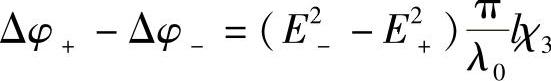
光学功率相差1μW就会导致相位差10^-6μrad，等效于0.01°/h的转动。实际上，这就要求这些装置能测量约0.01°/h的转动。光纤衰减很容易产生这个量值的光学功率差，越是远离线圈中心，越容易形成功率不相等。

利用方波调制激光能量可以解决该问题。在这种情况中，每种光束仅有一半时间受到另一光束的影响，所以式（10.17a）中的交叉乘积项会减小一半，有：

Δφ₊=Δφ_-

其他噪声源是光纤中的瑞利（Rayleigh）后向散射，产生一个相干的干涉信号，并且由于温度变化光纤面积也会变化。

尽管在旋转速度不小于0.1°/h时，这种装置具有简单和低成本的明显优越性。但是，所有上述问题使该装置很难在最低转速时有很强的竞争力。为了获得最高灵敏度，采用“最低配置”设计，如图10.16所示，确保整个系统几乎都由普通的倒易路径组成。在这种布局中利用集成光学是有利的。

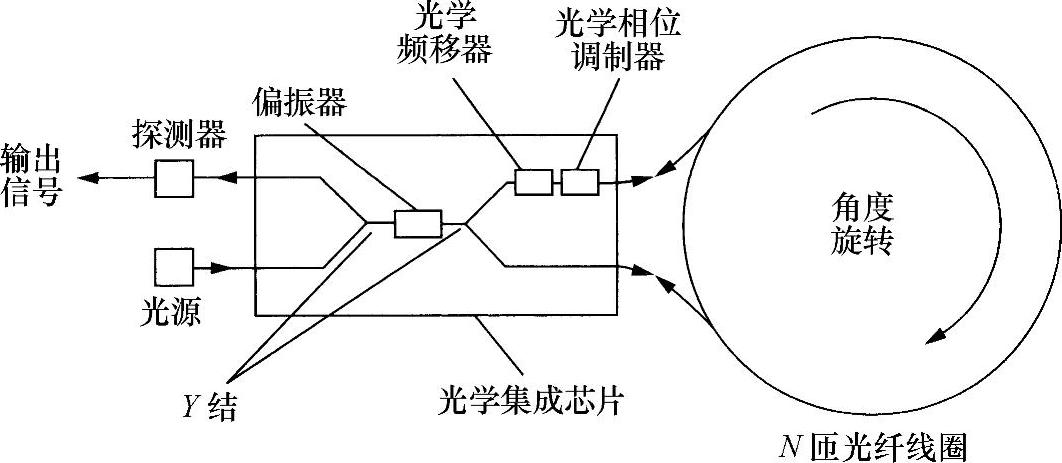
图10.16　“最低配置”光纤陀螺仪

利用集成光学芯片实现光的偏振和分束。（声光）移频器和相位调制器也设计在该芯片上，用以确定旋转方向，并保证检测偏压稳定在最大灵敏度位置。采用集成光学芯片意味着，该装置可以非常紧凑。已经制造出一个非常小的装置，封装在沙丁鱼罐头盒形状的一个箱体中（包括有诸如光学和电子功能的集成光学芯片，有时称为“光子学集成光学线路（Photonic Integrated-Optical Circuit，PIC）”）。

最低配置光纤陀螺仪的应用从弹道导弹、油井钻头的设置和控制，直到汽车导航系统，最后一种应用是特别有希望的增长领域。

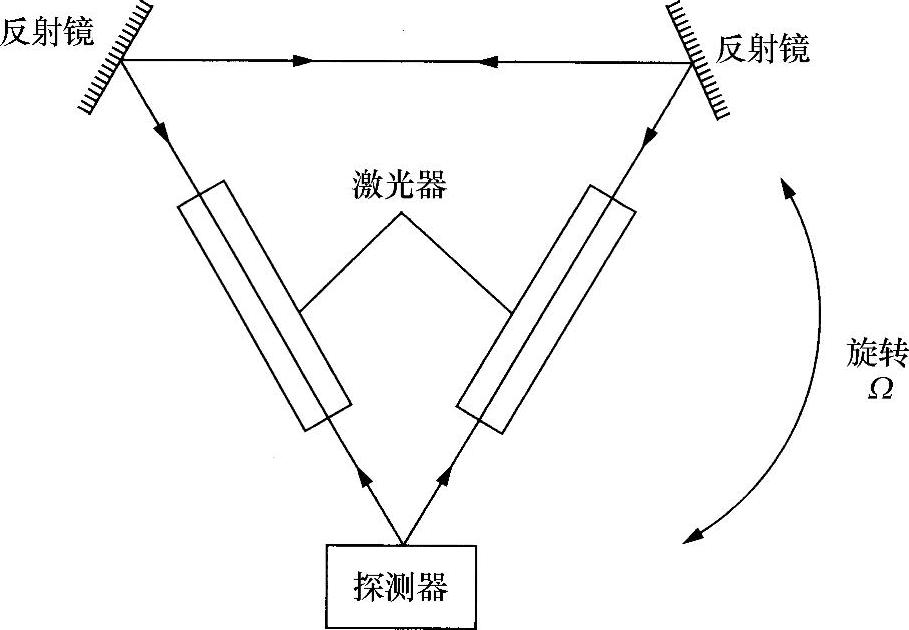
图10.17　环状激光陀螺仪示意图

光纤陀螺与图10.17所示的环形激光陀螺（Ring Laser Gyroscope，RLG）在许多应用中都是直接的竞争对手。这种装置利用同样的萨格奈克（Sagnac）原理，但不采用光纤；相反，采用一种三角激光腔，插入到诸如石英一类材料中，并填充激光增益介质（即He-Ne）。这种环形激光陀螺在两种反向传播激光模式中形成差频，这是一种由萨格奈克效应造成的差别——正比于旋转速率。

最近一段时间，尽管环状激光陀螺仪装置存在一定问题，但比光纤陀螺仪发展得更快。光纤陀螺仪有潜力与环状激光陀螺仪保持同等性能，但有更便宜的价格。（由于该陀螺仪包含更广泛的光子学内容，所以本章选择较详细地阐述该装置。）