光子学设计基础：集成光学光谱分析仪

本节需要的主题内容：

i）集成光学（本书第8章）

ii）声光调制（本书第7章）

iii）夫朗和费衍射（本书第7章）

iv）压电效应（本书第9章）

v）光电探测（本书第7章）

由于种种原因，常常需要对某给定波形进行光谱分析，这是确定波形中各频率分量振幅和相位的一种分析方法。

最经常分析的波形是电信号的形式。为了确定已知频谱的特定光源或过程所形成的分布，或者了解不同分布随时间变化的方式，就必须进行光谱分析。在军事应用中，经常需要通过典型的光谱特征区分飞机、潜艇或陆地战车，因为每种装备都会发射自己的声波或电磁波。利用其光谱也可以确定对其后续系统的影响。

在这些应用中，必须在一个比时间常数（能够表征光谱变化）小的时段内进行实时分析。尽管利用电子技术可以完成该任务，但太慢以至于无法接受。

在本书2.10节曾介绍过，远场产生的夫朗和费（Fraunhofer）衍射图恰恰是孔径分布函数的傅里叶变换（Fourier Transform，FT）（见本书附录Ⅱ）。由于傅里叶变换代表着某函数中存在的各种振幅和相位，所以正好可以利用这种变换。在本书2.10节已经看到，一种（例如）正弦形式的孔径分布在远场衍射图中恰好形成两条谱线，对应着确定正弦波振幅和相位的正负频率。(www.xing528.com)

可以使这种思想在光谱分析仪中充分显示其优势，在此需要知道与要进行光谱分析的波形相对应的衍射孔径分布函数。

讨论图10.8所示的结构。假设要分析的波形是一个具有适当量值的电压形式（如果需要，事先可将电压放大），施加在铌酸锂（LiNbO₃）层状结构中一个“叉指式换能器”上，即集成光学（Integrated-Optic，I-O）芯片上。通过隔行设置电极，该换能器通过压电效应，利用施加的电压造成铌酸锂材料交感神经式的膨胀和收缩。（再次回想起，在晶体材料上施加一个电场，就会与原子中控制原子间隔的电子键相干涉。所以，该间隔会随某选定方向的电场变化，也与具体的晶体结构有关，从而构成压电效应。）这种神经交感式伸张和压缩将在垂直于叉指电极方向发射纵向声波，并进入晶体。

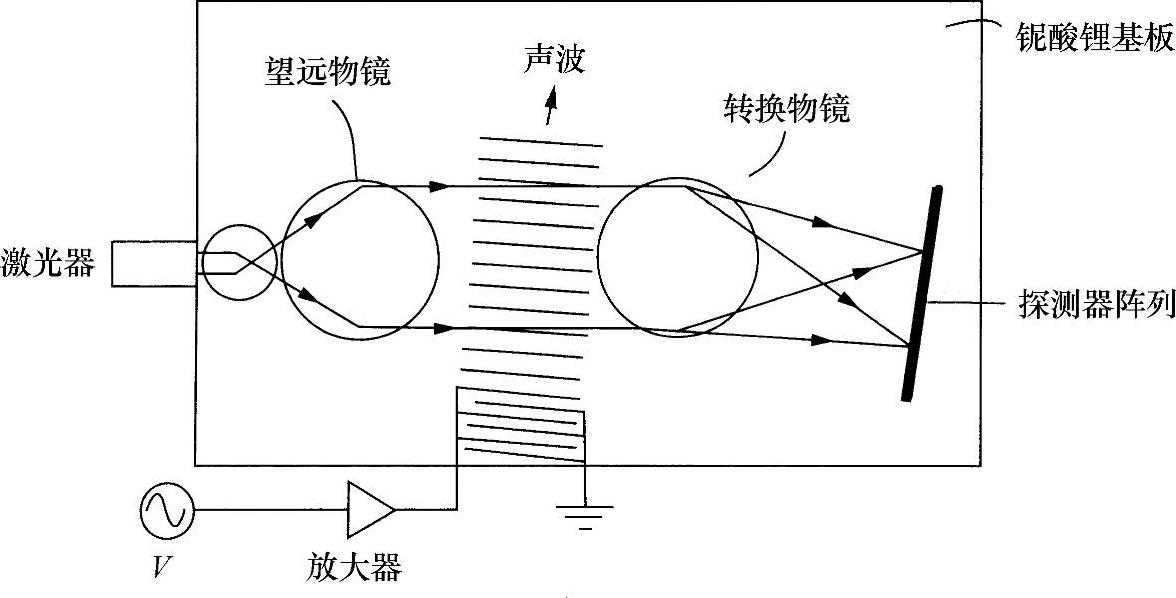
图10.8　集成光学光谱分析仪

由本书7.3.3节声光效应的讨论已经非常清楚地知道，折射率与介质密度有关，所以该声波将依次引起介质折射率的共变。与进行光谱分析的波形相对应，这种声波由此形成了所需要的衍射孔径。如果（见图10.8）激光器发出的平面相干光正常通过声波传播（如本书7.3.3节介绍的声光调制），则远场产生的衍射图便形成所需要的实时光谱分析。将远场衍射图投射到光探测器阵列上（见图10.9），使探测器阵列的每一个探测元与某已知衍射频率分量的位置相对应。由此，该阵列就提供了所需要的光谱分析。

必须记住本书7.3.3节讨论的声光衍射效应能够出现布拉格（Bragg）型或拉曼-奈斯（Raman-Nath）型的条件。毫无疑问，在较低频率时，拉曼-奈斯效应是主要的。然而，随着频率升高，在光束完全与其相交之前，衍射孔径已经改变形状，并属于布拉格效应范畴。当然，布拉格效应相对于入射角有多得多的选择性。所以，在较高频率时，需要更为认真的设计，使叉指换能器阵列设置有不同的角度。由于没有包含新的原理，所以在此不再做深入研究。

波形光谱分析方法的优点是，能够快速实时地并行完成不同频率分量的分析，可以在一个小型紧凑、轻而结实的集成光学组件上完成，对由冲击造成的光学错位不敏感，并容易大批量生产。显然，利用已经成熟的集成光学技术很容易将需要的所有分量都“写进”集成光学芯片中。这种光学处理技术只是利用光学/材料相互作用实现其目的方法之一；而在技术领域，就是众所周知的利用材料中各种线性和非线性光学效应的“光学信息处理技术”。显然，该课题是利用光学操作完成较为高级复杂的处理运算，以致最终形成非常先进的光学计算机先期技术，具有并行处理和高运行速度的所有优点。要非常认真地对待其未来的发展空间。

图10.9　集成光学信号监控开关