光纤测量电流，快速实现

本节需要的主题内容：

i）法拉第磁光效应（本书第3章）

ii）偏振光学（琼斯矩阵）（本书第3章）

iii）光纤的偏振性质（本书第3章）

iv）光探测器（本书第7章）

上一节已经讨论了一种光学装置，现在介绍光子学系统。通过该项研究就会发现，将光学与电子学知识相综合，会显示出设计方案的若干优越性。

全世界电力供应业（Electricity Supply Industry，ESI）存在的一个共同问题，就是对各类发电站生产电流的计量。生产出的电量在高压线网上分配给供应公司的用户（因为电压越高，在给定转换功率下电流就越小，因此电阻损耗就越小），必须对这种电流进行精确测量，从而确保对顾客使用的能量正确收费。同时，还要正确控制输电网，并快速显示故障条件，以采取合理的措施。

通常，是在称为变电站开关的配电接线盒处计量该电流，并且必须在几十万伏的高压母线上完成。

使用一次和二次感应线圈的普通电流互感器普遍应用于这种测量。但是，两组线圈之间需要代价很高的高压绝缘。并且，由于铁磁磁滞作用，它会出现饱和效应。这是因为存在着大的线圈自感应，还会有较低的带宽。图10.3所示为利用光子学技术测量高压电流的一种方法。

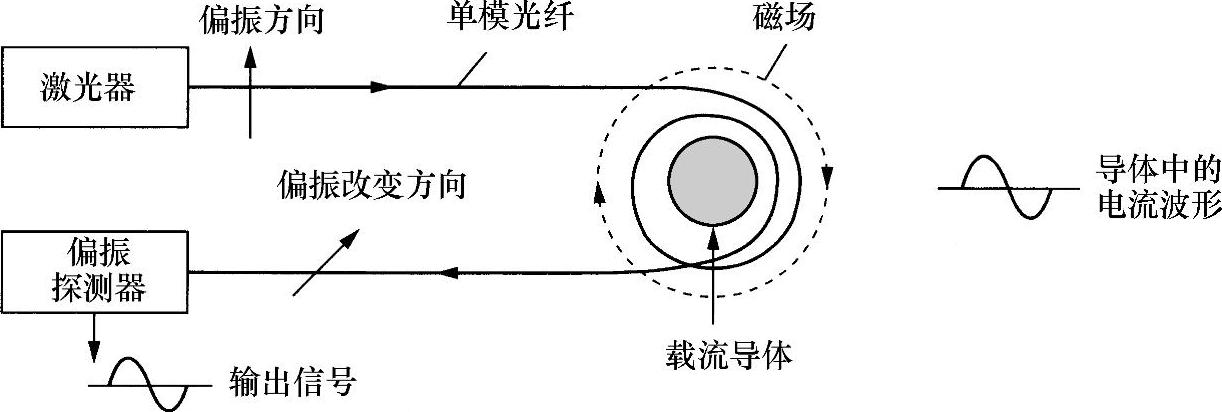
图10.3　光纤电流测量法示意图

将一段单模光纤（一种良好的绝缘体）绕着载流导线绕几匝。由半导体激光器发出的线性偏振光入射到该光纤线圈中。当光通过光纤线圈传播时，由于载流线圈中的电流作用，该光受到磁场影响。环绕电流的磁力线是圆柱形，将它围绕着导线扎成线圈时，则磁力线平行于光纤芯。因此，线偏振光传播时，便处于纵向磁场的作用之下，因而形成法拉第磁光效应。并且，偏振方向会发生偏转，偏转量正比于磁场及磁场作用的路径长度。正如本书3.10.2节强调的，这是一种由磁场感应产生的圆双折射。

偏振方向出现的总旋转正比于回路周围场的线积分，即

式中，V为费尔德（Verdet）磁光常数；N为光纤线圈的匝数；H为磁场；l为线路长度。

由基本的电磁知识知道，载流导体周围磁场的线积分恰好等于电流（安培串联电路定律）。因此，式（10.6）可以写为

ρ=NVI

式中，I为被测量的电流。

由于N和V是已知的常数，因此对ρ的测量就是测量I。这是一种非常方便的测量高压下电流的方法，理由是：

i）光纤是用一种电介质绝缘材料制成，在高压导线与（接地）指示点之间需要一定成本的绝缘。

ii）由于没有使用铁磁材料，所以没有磁滞效应。

iii）在熔凝石英材料中，磁光效应非常快（几乎是瞬时的），因此测量带宽非常大。

iv）很容易将光纤缠绕在高压导线上，因此安装非常简单。

如何实施测量ρ呢？假设，发射出的线性偏振光入射到线偏振器上，线偏振器的偏振方向平行于输入光的偏振方向（见图10.4a）。若没有磁场（ρ=0），所有的光都将通过偏振器（忽略内在衰减）。

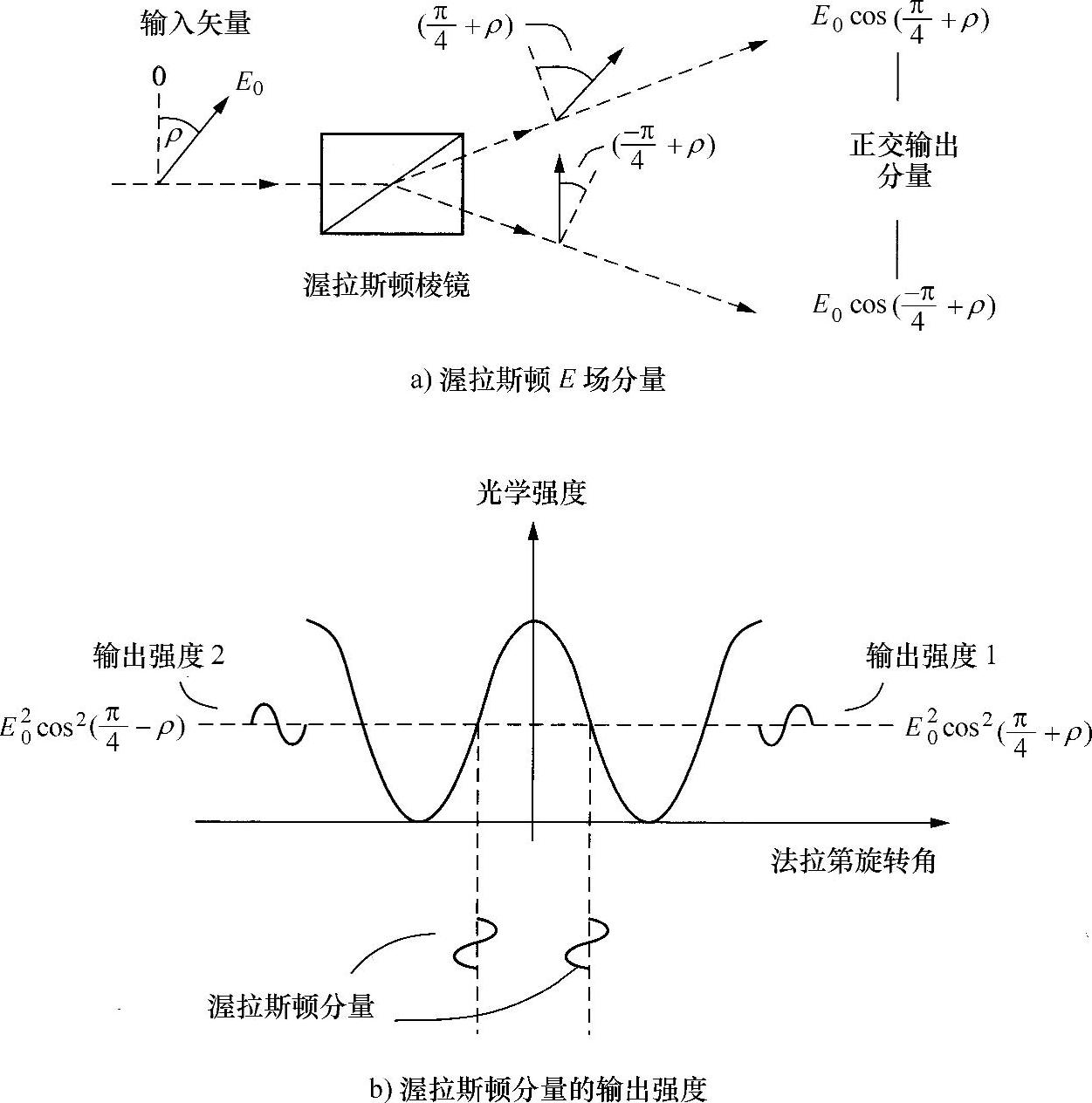
图10.4　电流信号测量过程中渥拉斯顿（Wollaston）棱镜的作用

假设，传播光束的电场振幅是E₀，所以，在没有电流时，是一个正比于E²₀的光强度通过。当有电流通过时，偏振使旋转一个角度l，所以只有一个场分量E₀cosρ通过偏振器，因此只要测量出与E²₀cos²ρ成正比的光强度，原理上就可以根据该强度推导出ρ。

然而，还有一种更为方便的测量ρ的方法。

假设，不使用简单的偏振器，而是使用渥拉斯顿（Wollaston）棱镜，其偏振轴与输入的偏振方向为±45°的角度。现在，从渥拉斯顿棱镜输出的有两种光强度（见图10.4b），即

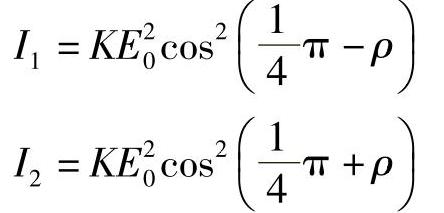
式中，K为通用常数。

分别探测两种强度（通过测量两个光敏二极管上的光功率，记住功率=强度×面积），可以很容易地设计出电子线路以实现下面功能：

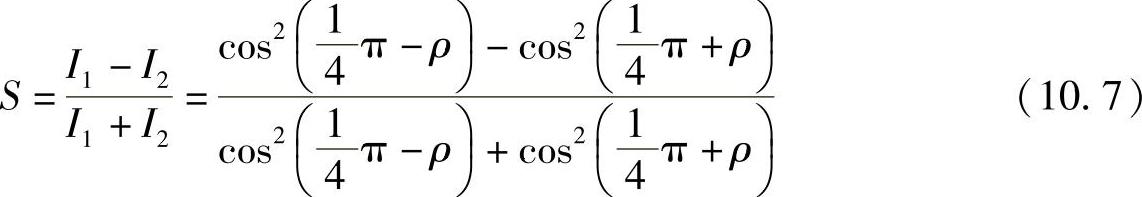
运算后得

S=sin2ρ

如果2ρ比较小（<<π/2），则

S≈2ρ=2NVI

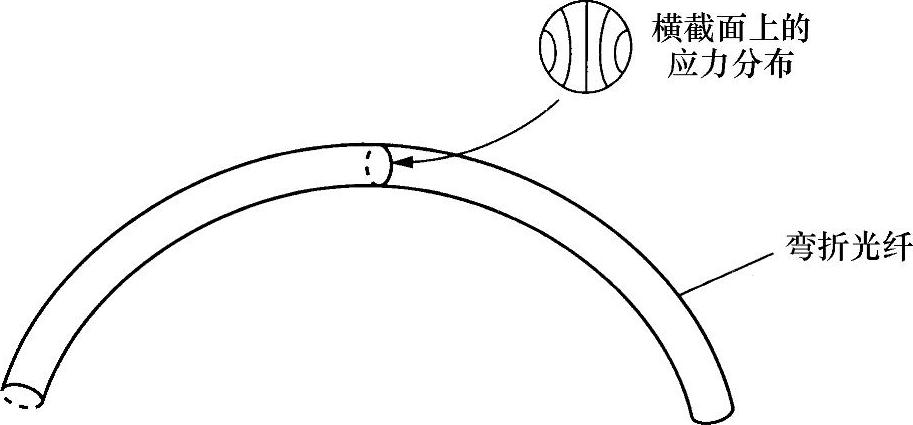
因此，在该条件下，S正比于电流I，与随时间变化的光强度（约等于E²₀）无关。利用这种方法测量电流有什么问题呢？首先，光纤必须缠绕在高压导线上，如果缠绕一根光纤，并是不对称缠绕（见图10.5），那么由于应力光效应，应力就会使折射率发生变化，从而引进线性双折射。已经知道，在线性双折射光纤中，只有两种线性本征模（即平行于双折射轴的那些线性偏振态）的传播不会改变形态。显然，在这种光纤中不可能保持旋转线性偏振态仍是线性偏振，将出现椭圆偏振态。这不仅取决于弯曲后的双折射，同时与沿光纤旋转的方式有关（与测量的电流有关）。

(www.xing528.com)

图10.5　光纤的弯曲应变

式（10.7）表明，S的值正比于两种渥拉斯顿输出（I₁，I₂）之差。然而，除了由于被测电流形成圆双折射外，该差值还与偏振椭球的轴有关（即与线性弯曲双折射有关）。例如，如果偏振椭球退化成一个圆球，即使电流不是零，S仍变成零。因此，这种弯曲双折射效应将明显地影响测量。

借助本书3.12节讨论的琼斯矩阵可以方便地使这种效应量化。当线双折射量为δ时，使偏振旋转一个角度ρ（具有圆双折射2ρ）的偏振元矩阵为

因为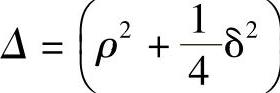，，则有：

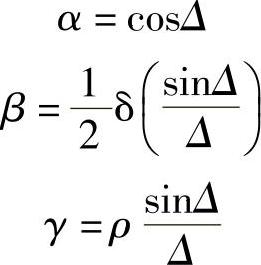
线双折射的快轴和慢轴取作矩阵轴（Ox，Oy）。由于ρ与δ之间的相互作用十分微妙，所以该矩阵相当复杂。δ对偏振态的影响取决于偏振态本身。例如，对平行于其中一个轴的线性偏振态没有影响，但是，如果该偏振态旋转45°，就会有最大的影响。由于有旋转角度ρ，所以方位会连续变化。由此可以得出结论：δ的影响也连续改变。

假设，输入到光纤线圈中的线性偏振光的偏振方向与其中一个双折射轴。例如Ox轴一致，那么就可以用下列向量表示：

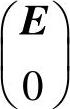
式中，E为电场。现在，可以将输出光的偏振态确定为

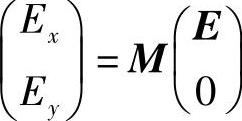
利用式（10.8）中的M（记住，E_s是复数），从而使式（10.7）中的S可以写为：

这就将测量问题定量化。首先，假设由弯曲引发的线双折射δ要比电流引发的圆双折射2ρ大许多（因此也比旋转量ρ大许多），在这种情况下：

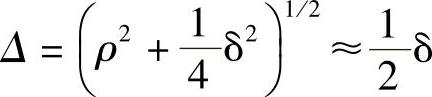
因此，由式（10.9）得

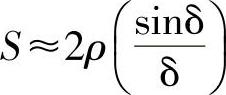
若δ>0，则S<2ρ，并且测量灵敏度会降低。实际上，这种情况要比简单地减少输出更糟糕，因为δ值与温度有关（因为温度与光应力系数有关），所以S也与温度有关。此外，振动也使δ减小（因为振动的压力会使光纤应变），因此S中将存在由于振动而感应的交流（A/C）噪声。对这些问题如何解决呢？

首先，保证弯曲直径要大（>0.5m），从而使弯曲双折射最小；其次，尽可能利用具有内在圆双折射的光纤（如石英一类的光学活性晶体）。有几种方法可以减小光纤中的圆双折射，其一是绕自身轴简单地缠绕（见本书3.10节）。在这种方法中，有：

2ρ>>δ

因此

Δ≈ρ

和

S≈sin2ρ

（实际上，此处出现的现象就是大量内在双折射造成的偏振态，非常快地沿光纤旋转，因此使线性双折射的影响完全被平均）现在，ρ为内在圆双折射（2ρ₀）和电流感应的圆双折射（2ρ_I）之和，所以有：

S≈sin（2ρ₀+2ρ_I）

根据本书3.10.2节的讨论知道，这两种成分的圆双折射有一个基本差别：ρ₀为倒易双折射，而ρ_I不是倒易双折射。从而意味着，如果光沿着光纤后向反射，就会围绕导体形成一段来回传播的线圈通路，内在倒易双折射（2ρ₀）将被抵消，电流感应产生的非倒易双折射（2ρ_I）将会加倍。因此，图10.6所示结构中若存在后向反射，就有下列关系成立：

S≈4ρ_I

这就有了另外一个优点，即消除了ρ₀对温度的依赖性（当扭曲形变产生ρ₀时，应变电光系数对温度具有一定的依赖性）。这种布局的优点是，只安装一端，非常方便（见图10.6）。

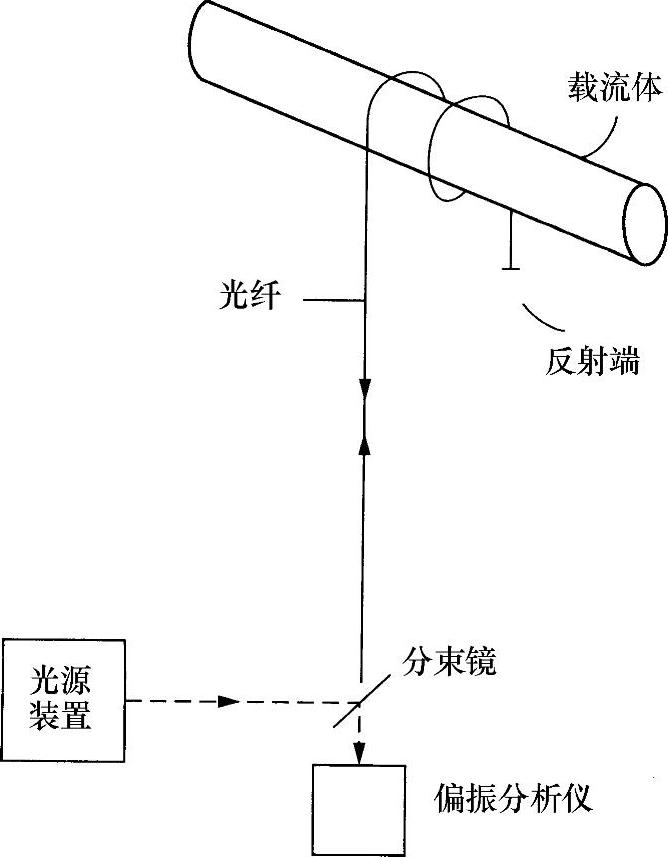
图10.6　单端光纤测量电流装置的安装示意图

可以看出，通过对偏振光学的精透理解，可以设计出一种非常满意的、没有温度和振动效应影响的装置。这样既便宜又方便地完成非常重要的测量。以此原理为基础的装置已经在电力行业应用于各种诊断和测试程序，快速和容易安装是该装置非常大的优越性。

图10.7所示为一种特别有意义的光纤测量电流的应用实例，由于不需要内在圆双折射，所以，甚至无需使光纤扭曲。

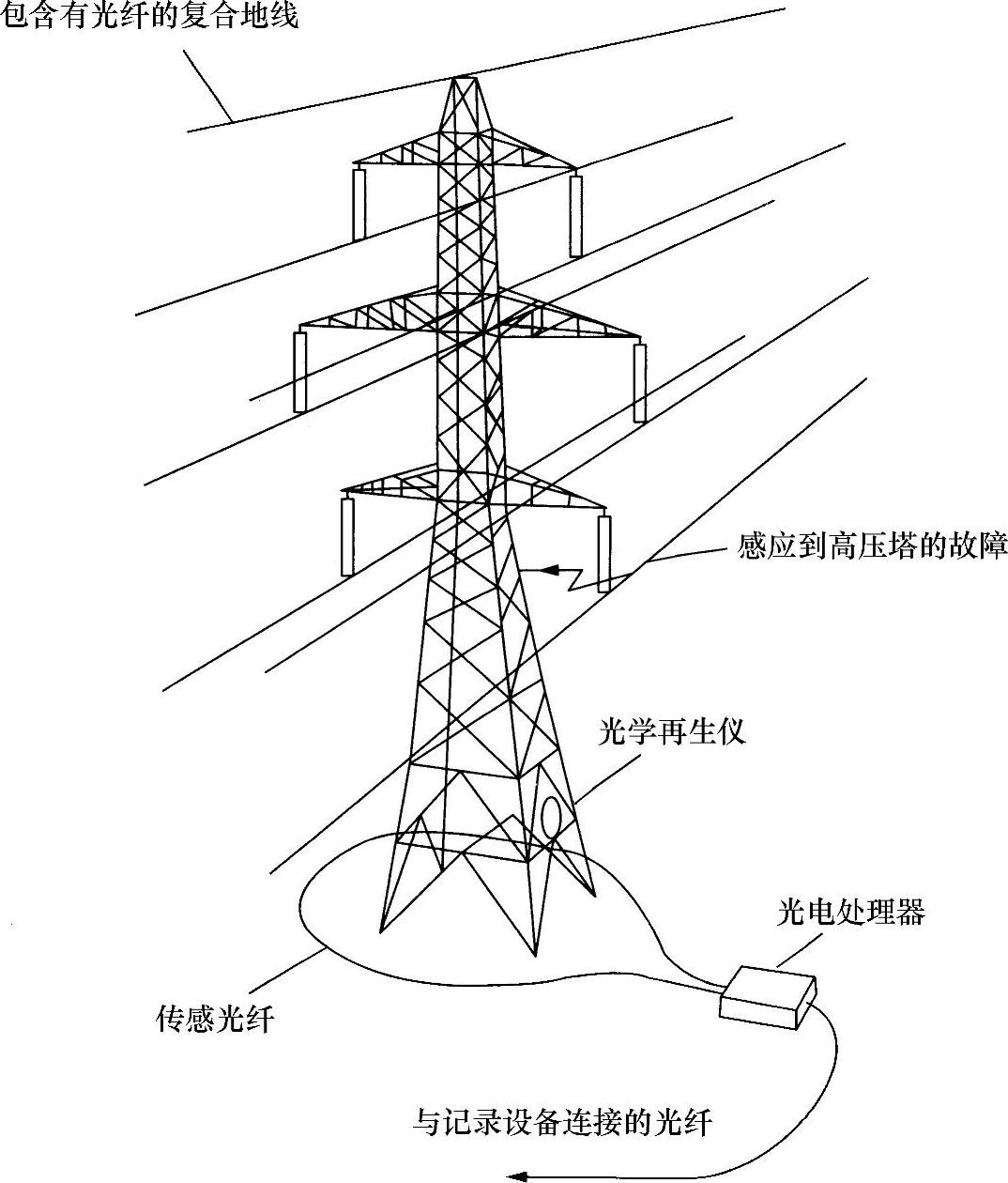
图10.7　“塔基”式光纤测电流装置

一根光纤环绕一座高压输电线路铁塔，测量当一根高压线与接地塔之间出现短路时流入地内的电流。例如，当闪电直接击中该相线而出现这类故障时，采用这种测量可以对传输到地内的电流量提供非常有价值的信息。利用任何其他方法都很难对这种电流进行测量。实际上，用常规的电流互感器进行测量是不可能的。在这种应用中，由于线圈直径非常大（约10m），所以弯曲双折射不是问题；由于故障的机械冲击沿传输塔传播到地面之前就已经完成了测量，所以振动也不是问题；在如此短的时间内温度漂移可以忽略不计，所以温度依赖性更不是问题。另外，其优点是，带宽相当大，足以保证短周期（约1μs）波形可以精确地被复制，并且能够在几分钟内安装和拆除光纤。这是一个以巨大优势将光子学（或任何其他）系统或装置的性能与具体要求相匹配的良好例子。

这是对光纤测电流装置带宽的注释：磁光效应的速度并不是限制因素，而带宽受限于光通过光纤环路所耗费的时间。显然，小于该时间段就不能完成该测量，因为在这段时间内不可能实现完整旋转。那么，一个循环或许是最优结果？事实未必如此。由式（10.6）可知，测量灵敏度未必正比于匝数。再次遇到带宽与灵敏度之间常见的问题：对上述的任何一种技术，其乘积都是一个常数。进行折中（或者“平衡”）是系统或设备设计师设计技巧的核心。