增透膜与减反膜：光子学设计基础

本节需要的主题内容：

i）多波干涉（本书第2章）

ii）菲涅尔电介质公式（本书第2章）

iii）材料色散（本书第4章）

光子学系统通常包含有许多诸如透镜、滤光片和偏振器之类的光学组件，其中每一种都含有一个或多个空气/玻璃（或其他光学材料）界面。当垂直入射时，根据菲涅尔公式式（2.13c）知道，两种介质（1，2）的界面处反射光与入射光的强度之比为

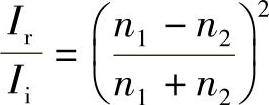
式中，n₁为使用波长下第一种介质的折射率；n₂为第二种介质的折射率（见图10.1）。这表明，若是空气/玻璃界面，n₁约为1，n₂约为1.5，就有：

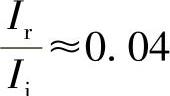
所以，在每个表面约有4%的光能损失。例如，一个照相物镜，具有两个这类表面，大约有8%的损失。在低光照条件下，这是一个相当严重的缺点。

现在，讨论图10.2所示的结构，由第三种电介质材料制成的薄膜层插在两种原始材料之间。令插入的薄层材料折射率为n₃，厚度为d。假设，一束（单色）波在介质1中向着该薄层传播。该波会在1和3的界面处发生反射，在3和2界面处发生另一次反射。如果能够使这两次反射相消干涉（即彼此相消），则由前端1和3界面产生的反射将被消除。现在计算发生这种现象的条件。在本书2.9节，已经讨论过振幅逐渐减小的多次反射的相关课题，这些内容在此仍然需要。

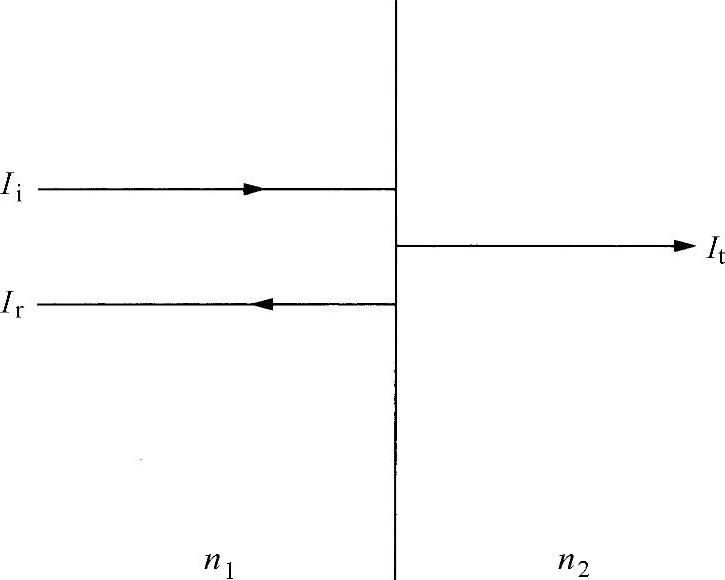
图10.1　电介质材料界面处反射示意图

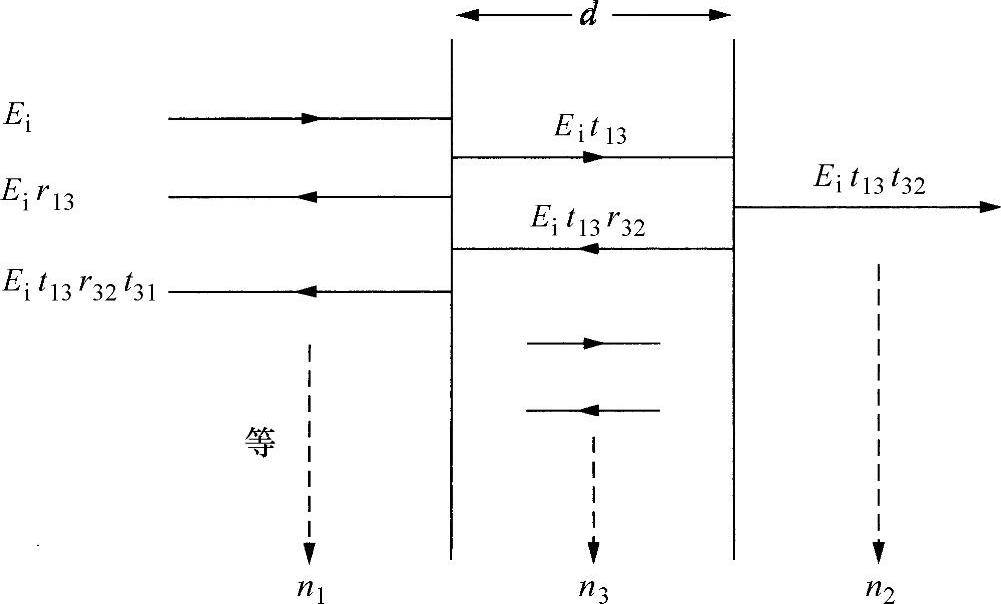
图10.2　三种电介质材料界面处反射示意图和术语表示法

假设，入射光学电场为E_i，在1和3界面处发生第一次反射，根据菲涅尔式式（2.13a），反射光电场可以写为

透过的光波为

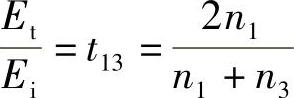
又将被3和2界面反射，并且，在前表面再次出现时会有相位延迟φ，即

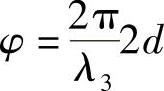
式中，λ₃为材料3的光学波长。两次通过厚度为d的薄膜材料进行传播。该波在3和1界面处部分透射和部分反射。伴随着反射的透射波振幅为

E′_r=E_it₁₃r₃₂t₃₁exp（iφ）

根据菲涅尔公式式（2.13a）和式（2.13b），有：

反射分量将由于3和2界面的反射而另外两次通过第三层材料传播（见图10.2），并形成反射波进入到材料1中，其振幅为

E″_r=E_it₁₃r₃₂r₃₁r₃₂t₃₁exp （2iφ）(www.xing528.com)

显然，这种过程还会继续，第n次波反射回到材料1中，有：

E_r（n）=E_it₁₃r₃₂t₃₁（r₃₂r₃₁）ⁿexp（inφ）

因此，反射回材料1的总波振幅为

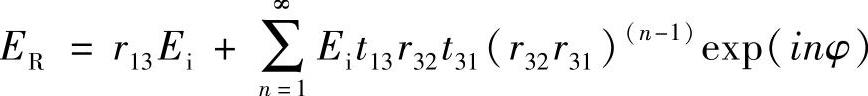
求和项是一个简单的几何级数，所以得

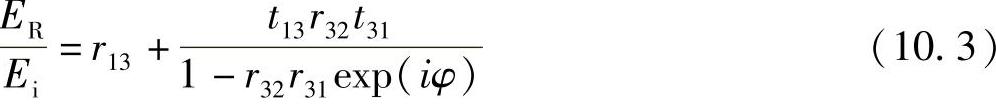
假设，第三层介质的厚度d是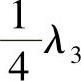的奇数倍，那么两次通过该层传播的光将有π的相位延迟，从而使该层内的连续反射被消除。为此，要求φ满足下列条件：

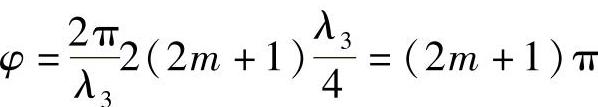
式中，m为正整数。

因此有：

exp（iφ）=-1

式（10.3）变为

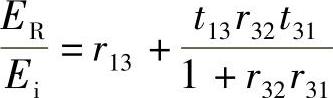
根据式（10.2）代替系数r和t得

由该公式明显看出，令n₃满足下式就可以消除反射波：

实际上，有很少几种材料能满足式（10.5）右边的折射率，并具有增透膜（或减反膜）需要的物理性能。若是玻璃/空气界面，则有：

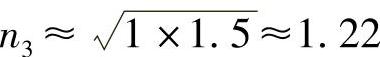
为使膜层具有一定硬度并对玻璃有良好的粘附性，使用n₃=1.35的冰晶石（氟铝化钠）或者n₃=1.38的氟化镁材料。

在干涉法控制下，将“增透（blooming）”膜层真空蒸镀在玻璃透镜表面。当反射波在选择的波长下消失便终止镀膜过程，对于诸如照相物镜一类的可见光光学组件，选择可见光光谱范围的中心波长（约550nm）作为监控波长。

当然，由于材料具有色散，其折射率随波长变化，所以式（10.5）只能精确地满足一种波长。

在波长550nm附近消除绿色反射光意味着，人眼可以观察到浅蓝红色。利用增透膜可以使整个可见光光谱的总反射率从4%减小到约1%。并且，正如前面强调的，对于许多灵敏的光学系统，如照相机、望远镜、显微镜和窄带光学滤光片，这是最常用的一种器件。

一些有关波相干的简单思想在这个种情况中产生了很有价值的实用效果。