光子学设计基础及孤子现象的应用

如果对光学孤子（或孤波）没有进行简要讨论，那么在“基础知识阶段”无需考虑非线性光学的问题。一个孤子就是一种“孤波”，一个波脉冲，即使介质中存在群速色散（Group Velocity Dispersion，GVD），这种波也能够长距离传播而不会改变形状。因此，在长距离光纤数字通信中有巨大的应用潜力。

孤子并不局限于光学，是非线性薛定谔波动方程的一组特定解，表示色散介质中随时出现非线性波运动的概率。在1834年，首次发现了沿着连接苏格兰爱丁堡和格拉斯哥的大运河传播的大振幅水波（这先于其他理论形成之前，并且一定早于薛定谔确定其波方程式之时）。1834年夏天，一位苏格兰的土木工程师John Scott Russell正在大运河旁边训练马匹，注意到马拉驳船突然停下时形成的波脉冲。这种波在完全不改变形状和幅度情况下传播。Russell骑在马上跟踪了2km，发现该波是如此令人费解地稳定，最后证明是一种水波孤子。在物理学的许多分支学科中，也陆续发现了孤子。实际上，无论何处，只要存在波的运动，所有恢复系统都能够被驱动成为非线性态。

对该现象的详细数学分析比较复杂，但基本思想简单直接，并且是根据已经讨论过的思想得出的。本书4.3节曾讨论过群速色散，本章前面内容（即9.6.2节）也介绍过自相位调制。将这两种思想组合在一起，就可以理解孤子的概念了。

如本章9.6.2节所述一样，令一束具有高斯强度分布的光波脉冲通过一种色散介质。由于该脉冲光源具有非零光谱宽度，群速色散将对该脉冲作用使其变宽；正群速色散会使较低频率首先输出，负群速色散使较高频率首先输出。显然，在这两种情况下，脉冲都被展宽。然而，如果同时存在自相位调制，根据式（9.9b）的结论知道，在脉冲后缘会形成较高频率，前缘形成较低频率。若这种效应发生在负群速色散中，那么脉冲后缘将易于接上前缘：脉冲将被压缩。很容易看出，在一定条件下，这种压缩效应可以精确地平衡由光源的光谱宽度造成的扩散效应，并且整个传播过程的脉冲宽度仍然保持不变。

的确能够达成这种平衡，结果形成孤子，图9.20给出了该形成过程。

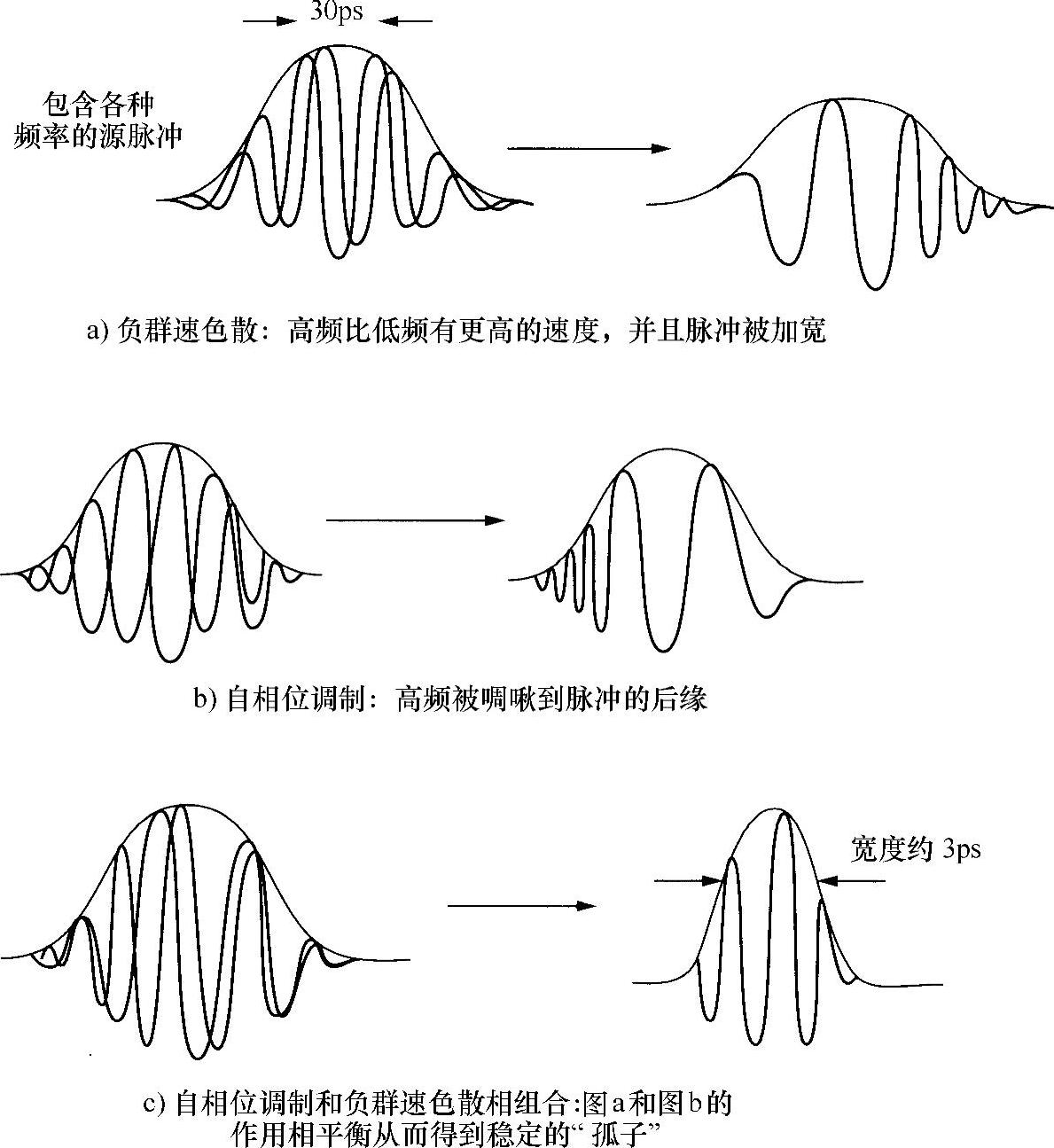
图9.20　孤子形成的基本过程

光纤中已经观察到孤子（见图9.21），并导致光通信系统具有不寻常的带宽与距离的乘积，或许高达10000GHz·km。然而，该理论表明，孤子在有损介质中是不稳定的。此外，当它们靠近至约10个脉冲宽度时，易于相互吸引。显然，这些性质限制了它们在通信领域的应用。(www.xing528.com)

图9.21　测量出的由光纤发射的孤子

然而，其发展潜力仍然非常大。毫无疑问，对孤子的研究还在继续。

产生孤子效应的理论包括高斯脉冲光束与正群速色散的相互作用。图9.22所示为自相位调制与正群速色散介质对这种脉冲光谱的影响，可以看出，其结果是线性啁啾（Chirp）有更宽范围（见图9.22c），频率线性地从脉冲前缘变化到后缘；此后，如果该脉冲传输到一个纯负的群速色散介质中（另一束光纤中），就可以非常强烈地被压缩。利用这种方法，在波长620nm条件下，已经得到小至8fs（即8×10^-15s）的脉宽，这种脉冲仅包含4个光学周期。

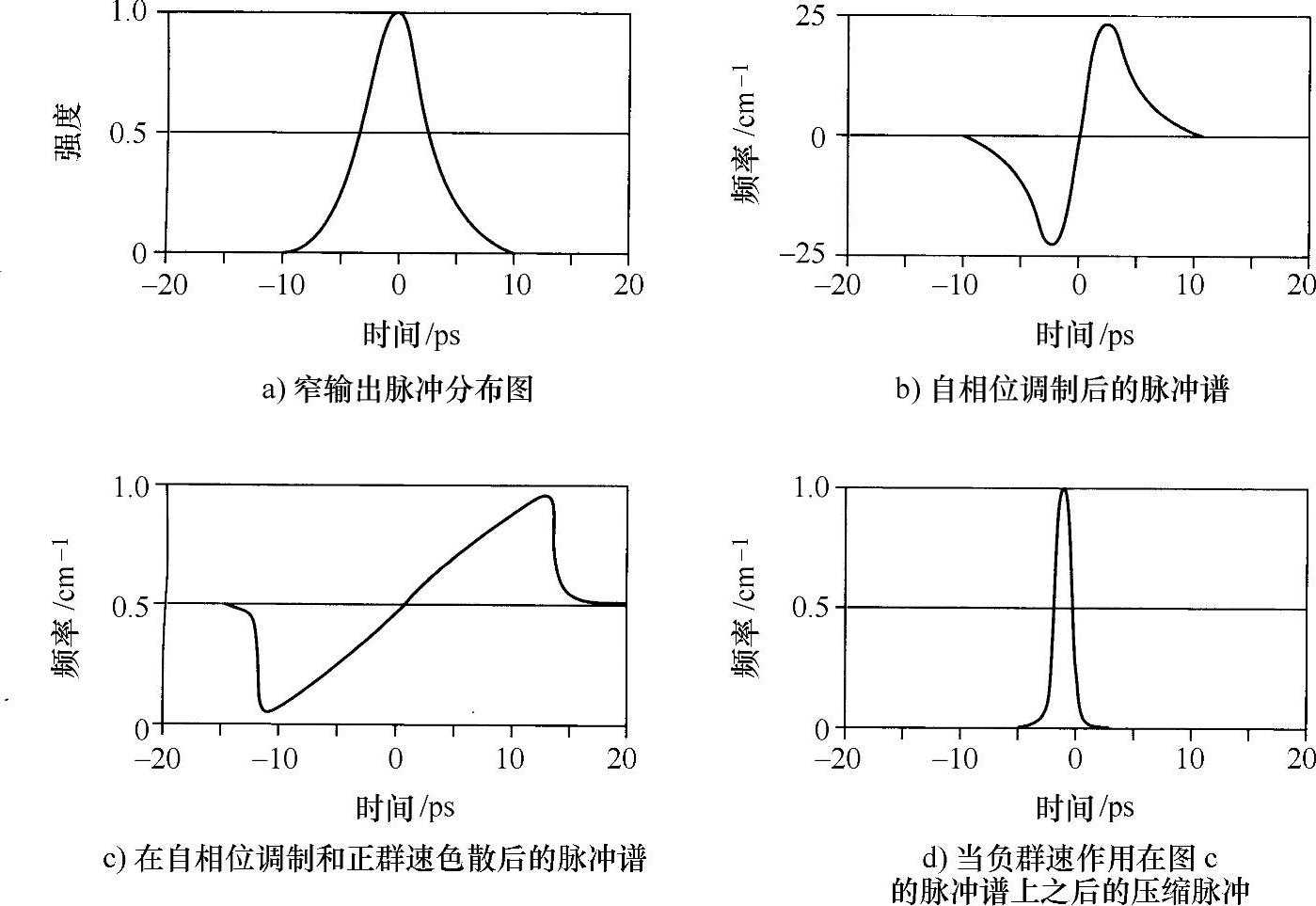
图9.22　利用自相位调制技术及正负群速色散对脉冲进行压缩

利用这类脉冲可以研究，诸如非常快速的分子变化过程、单原子化学反应及非常快的开关现象。