布里渊散射在光子学设计中的重要性

布里渊散射是泵浦激光和传播介质整体移动之间相互作用的结果。整体移动有效地在介质中形成一种声波，因此这种现象可以看作介质中传播声波所形成的布拉格类散射（见本书7.3.3节）。

按照量子机械论术语，可以采用与拉曼效应相同的方式解释这种效应。两个效应基本上是一样的，惟一区别是，现在的激发能量不是分子振动/旋转，而是整块材料的移动，这需要定量确定整体的运动。在该情况中，相关的量子称为“声子”。其余的解释都相同。

然而，由于是处于不同范畴，物理量的值也完全不同，相互作用的程度更强，带宽更窄，并且由于该介质是统一的整体进行移动，所以，从声学观点看，即使在非结晶形介质中，相位匹配条件也非常重要。

若是布里渊散射，初始的最佳方式或许是根据光学泵浦（激光）和声波在介质中相互作用的经典理论进行理解。这正是下面将要采用的研究方法。

如果一束声波在介质中传播，由于应变光学效应，应力变化会引起应变变化，随之使介质的折射率发生变化。之前处理声光调制问题时（见本书7.3.3节）遇到过这些效应。当温度高于绝对零度时，由于分子处于热运动状态，所以介质中总会存有声波，并且随之发生的动态相互作用会将能量耦合到结构的自然振荡模式中。因此，一束正在传播的光波（泵浦激光）会由于这些折射率的变化发生散射（即光子-声子散射）。这些效应将形成自发散射，而且由于声波的能量较低，所以这种散射会在非常低的水平上发生。

然而，随着泵浦激光功率增大，其中的部分能量可能因沿同一路径传播的声波而导致向后散射，或者向前散射。当然，声波速度有一个确定值，与介质特性有关。

实际上，激光辐射一直受到称为移动布拉格衍射光栅的影响而形成后向散射，所以向后散射的光学辐射会有一个高于或低于泵浦频率的多普勒频移（见图9.14）。

存在多普勒漂移的波与前向传播的激光辐射相干涉，在介质中生成光学驻波。由于存在多普勒频差，该波恰好以声速通过介质（利用解析方法可以简要地得到证明）。

如此形成的驻波将在腹点处有大的电场，以及在节点处有小的电场（见图9.14）。

无论何时对某种介质施加一个电场，随之会对介质产生一个机械应变。原因是上述电场破坏了固结介质的分子间的作用力，造成介质膨胀或收缩。该现象称为电致收缩。并且，正如所料，不同材料的量值完全不一样。

该情况下的电致收缩结果，是形成一个与光学驻波一致的声波。因此，后向散射波形成一个移动的声衍射光栅，并进一步产生后向散射。然后，泵浦波和多普勒漂移散射波相组合从而形成以声速可以前后移动的衍射光栅。三波相互作用中的任何一种波都是稳定的，前向传播的声波产生斯托克斯后向散射信号，后向传播的波产生反斯托克斯信号，整个自我维持系统构成了受激布里渊散射（Stimulated Brillouin Scattering，SBS）现象。为了理解并更好利用这种现象，必须对上述思想进行量化。

以速度v移动的声波产生的多普勒频移由下式给出：

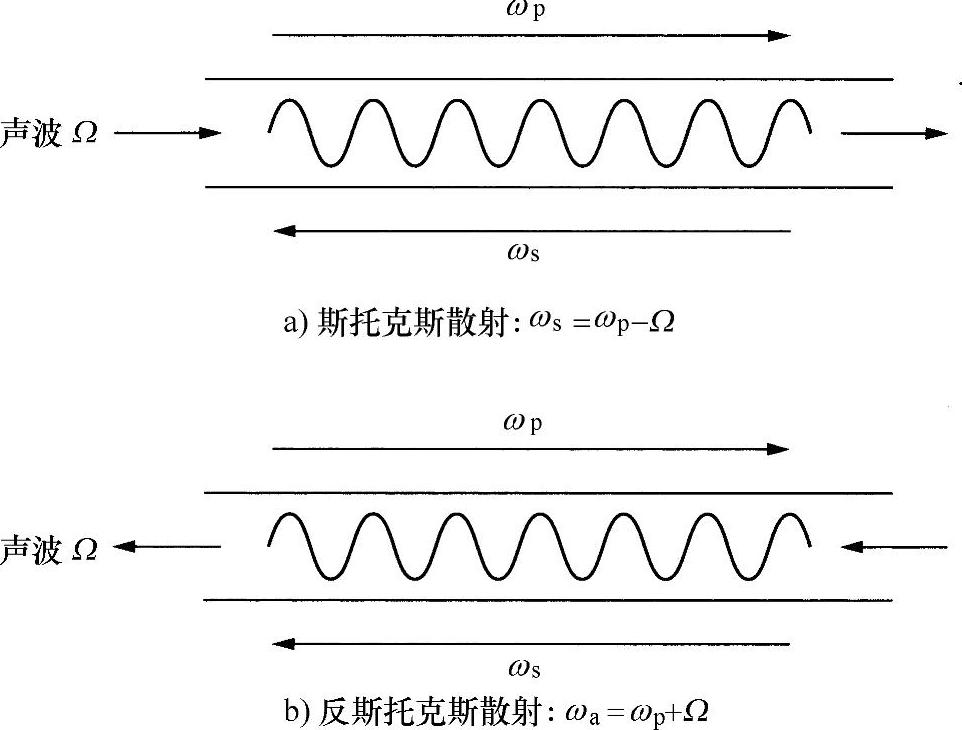
图9.14　光学纤维中基本的布里渊散射过程

式中，δω为角速度位移；ω_p为光学泵浦的角频率；c为介质中光速。

对于频率分别为ω_p和ω_B的前向传播（泵浦）光波和后向传播（散射）光波之和，可以写为

S=E_pcos（ω_pt-k_pz）+E_Bcos（ω_Bt+k_Bz）

经过运算，得

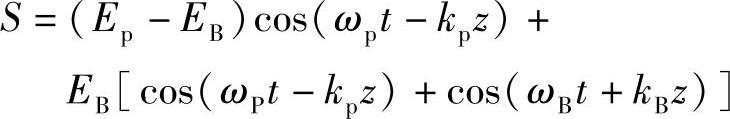
即

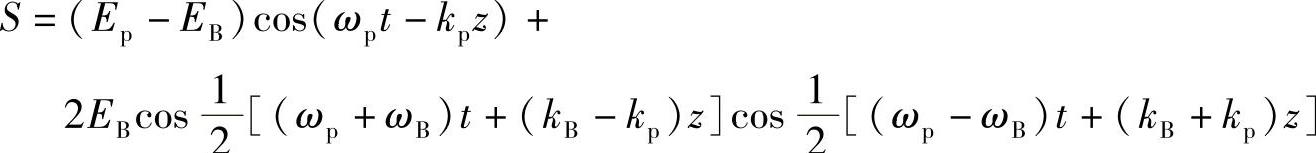
该表达式代表沿Oz方向传播的波（第一项）加上一个驻波（第二项）。驻波振幅按照下式规律变化：

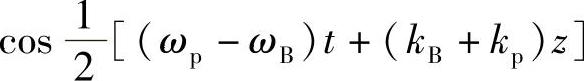
从而构成按照下面速度运动的一个包络线：

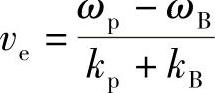
由于k_p=ω_p/c和k_B=ω_B/c，并且δω/ω_p非常小，所以(www.xing528.com)

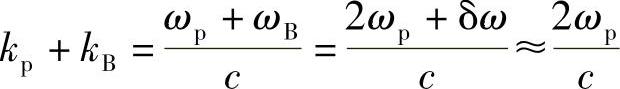
因此，k_p+k_B≈2k_p，并且根式（9.16）有：

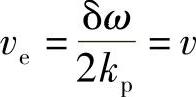
因此，驻波是以声速传播。

另外，由于δω/ω_p<<1，所以，对于一阶近似，在两个传播方向，驻波相邻腹点之间都有相同的距离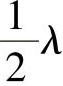p，这（即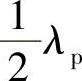）就是声波。

现在讨论匹配条件。能量守恒要求（见图9.15）为

δω=ω_p-ω_s=ω_a-ω_p=Ω

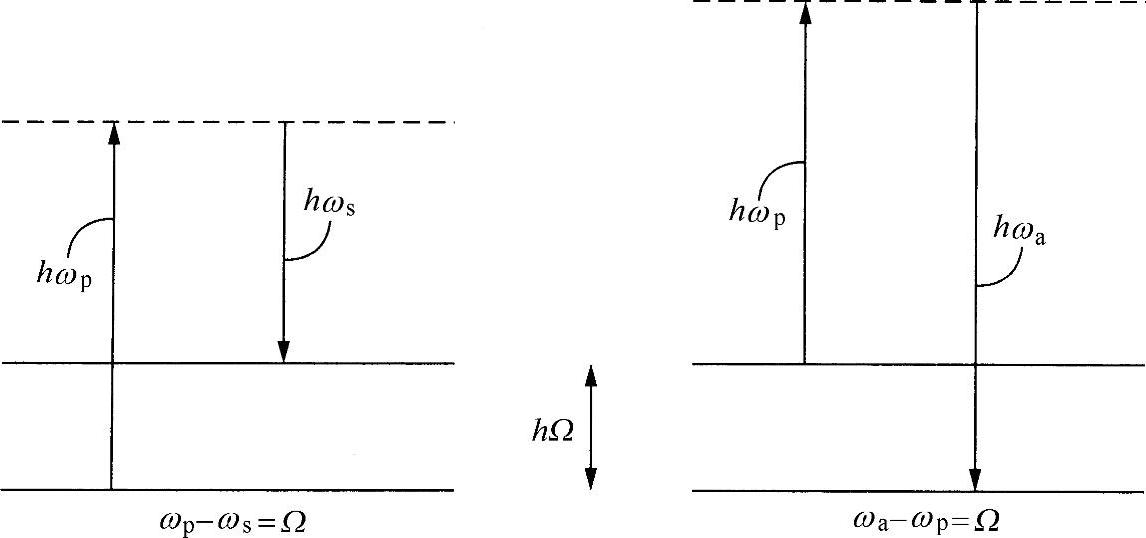
图9.15　布里渊散射的频率关系

式中，Ω为声角频率；p、a和s分别代表泵浦、反斯托克斯和斯托克斯分量。动量守恒要求为

q=k_p-k_s=k_a-k_p

式中，q为声波数。如果θ是泵浦光传播方向与任一散射波传播方向间的夹角，就有下面关系式（见图9.16）：

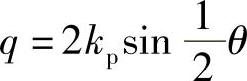
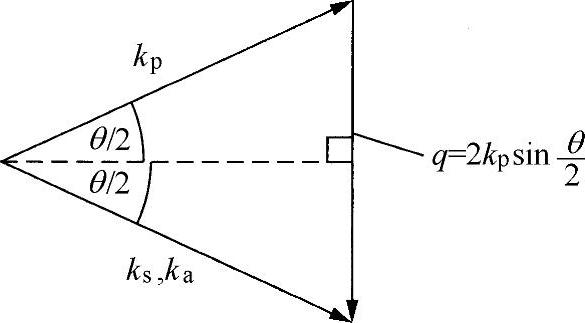
图9.16　布里渊散射的动量守恒

对于光纤，若是一阶近似，只有两种可能的θ值：0或者π。如果θ=0，则q=0，不会出现声波；若θ=π，则q=2k_p，声波波长等于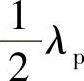，这就是本节要讨论的情况。因此，声波波长是光泵浦波长的1/2。斯托克斯或反斯托克斯频移的量为

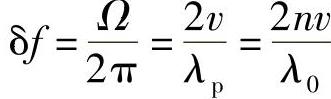
式中，λ₀为自由空间的光波波长；n为光纤介质的折射率（该结果已经从多普勒频移公式得出）。若是石英材料，λ₀=1.5μm，可以确定，δf约为11.5GHz。因此，布里渊效应中的频移要比拉曼效应的频移小两个数量级。

光纤布里渊后向散射的一个重要参数，是与之有关的带宽。该带宽取决于声波的衰变时间，在这些频率下约为5ns。因此，对于声波的相干散射，光波本身必须保持约5ns的相干。对布里渊效应，这意味着光学带宽为100MHz。即使是激光光源，这也是一个窄带宽，所以一般地某种光源中只有少部分光会出现布里渊后向散射，这就解释了为什么通常主要是拉曼散射的原因。即能够利用普通激光光源发出的更多的光。然而，对于低散射，尤其是相干光通信系统（见本书10.10.4节），使用远比100MHz小得多的光学带宽，因此布里渊散射就是传输功率大小的限制因素。对于13.6km的光纤长度，使用分布反馈式（Distributed Feedback，DFB）激光器发出的具有1.6MHz光学带宽的光束，已经测量出受激布里渊散射的阈值仅有5mW（见图9.17）。对光源发出的光进行相位调制可以抑制受激布里渊散射。对于相长后向散射，没有必要要求相位具有相干性，因此，可以传输更高的功率。这对于相干光通信系统^[3]具有非常大的优越性（见图9.18a和图9.18b）。

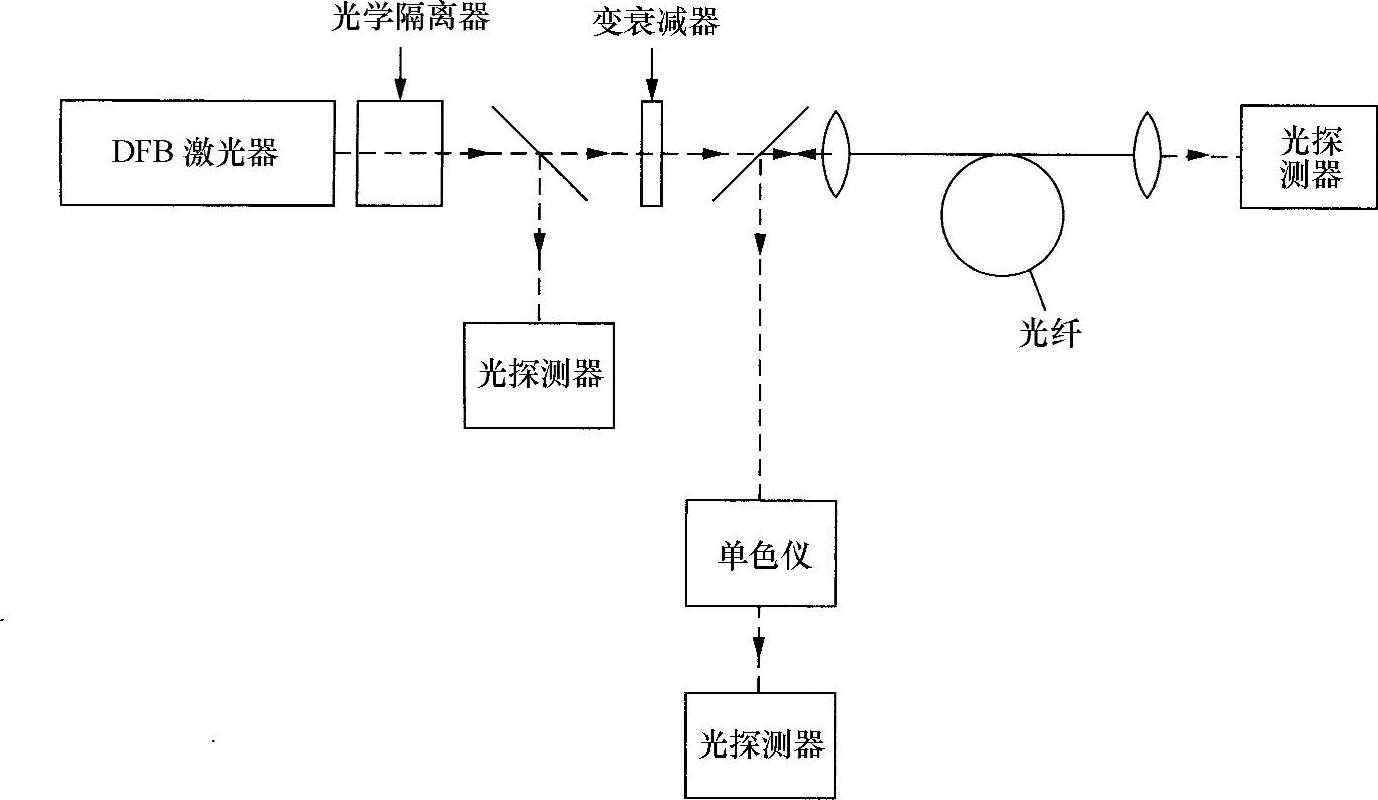
图9.17　观察光纤中受激布里渊散射的示意图^[3]

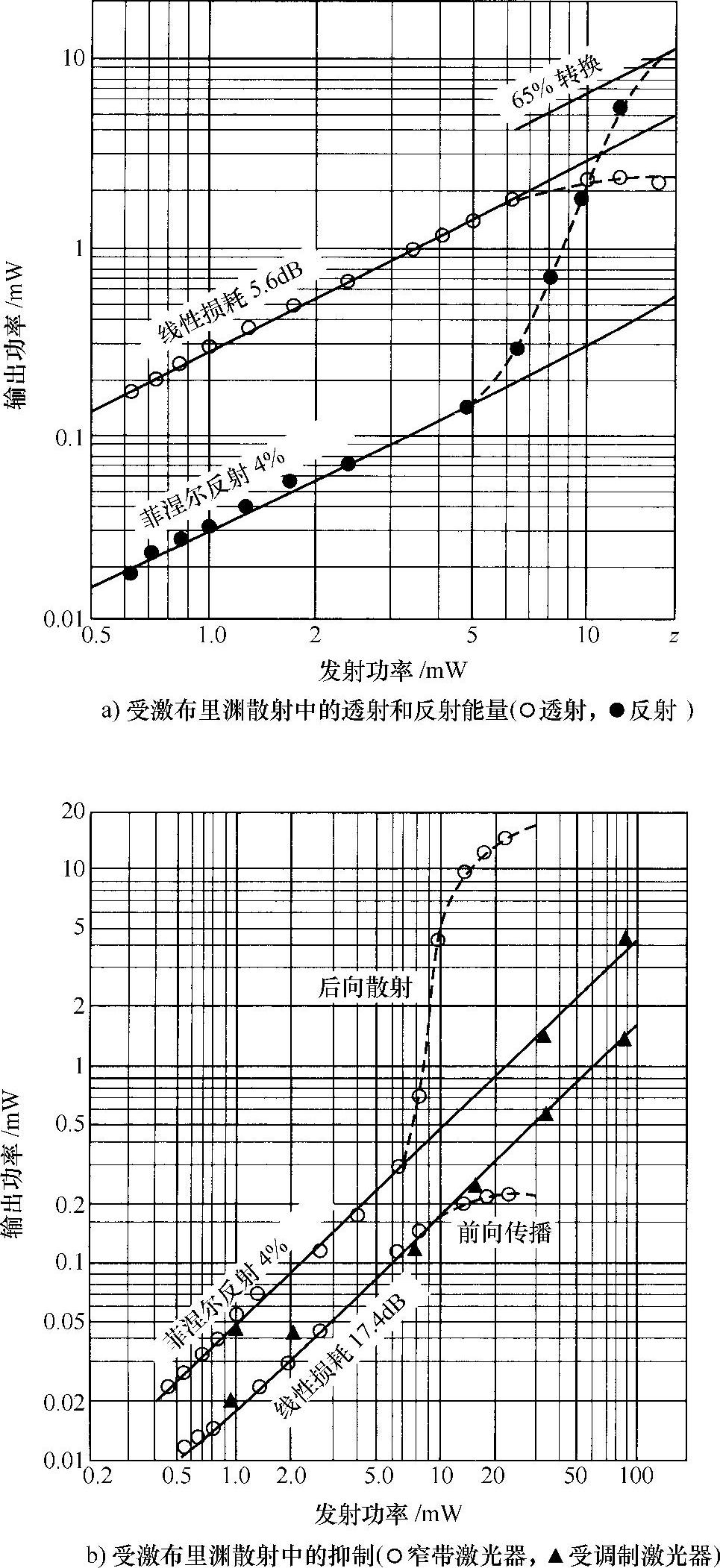
图9.18　光纤中受激布里渊散射对功率的依赖性和抑制^[3]

根据拉曼效应可以设计出布里渊放大器和振荡器（见图9.19）。它们优于拉曼放大器和振荡器，主要优点是频差非常小（约为10GHz），因此可以采用电子而非光学滤波和探测技术；并且带宽非常窄（<25MHz）。后面这种优点使布里渊放大器非常适用于相干光通信系统中光学载波的放大，不同于调制边带的方式。

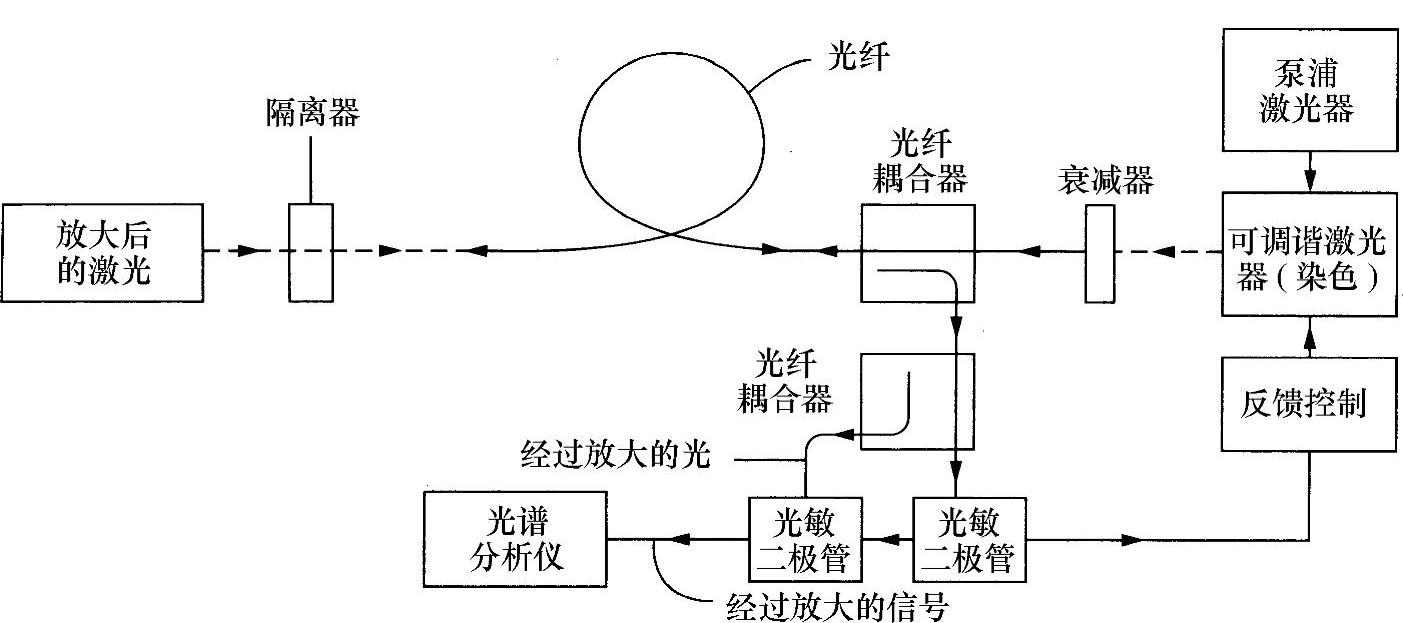
图9.19　受激布里渊放大器的示意图