光纤拉曼效应：光子学设计基础

众所周知，光纤允许长距离高强度的光路相互作用。因此，应当比较容易观察到其中的拉曼效应，尤其是受激拉曼效应，的确就是这种情况。

光纤由一种非结晶介质，即熔凝石英制成，在不同强度和不同方位的化学键接中有各种振荡频率和旋转频率，因此有一个很宽的拉曼辐射光谱（见图9.11）。

图9.11　石英的拉曼光谱

宽光谱放松了对相位匹配的限制，原因是每种散射大部分都与相位无关（因为结构是随机的），由此产生的强度简单地就是单个中心散射强度之和，并且对任何方向都是正确的（在本书4.2节已经讨论过随机散射体的理论）。在多模光纤中（除单模光纤外），由于不满足相位匹配条件，无需使泵浦波的相位具有相干性，所以可以相当容易地观察到非结晶石英中的拉曼散射过程：如同随机散射中心的贡献量一样，所有模式的这种随机贡献量都可以非相干地相加。可以利用多模光纤的另外一个优点，就是比较容易使大泵浦功率入射到光纤中，因而形成高拉曼辐射。

正如介绍过的，当泵浦激光信号非常强时，有可能在光纤中产生受激拉曼辐射。此情况下（与泵浦受激后的自发衰退相比），会产生大量的斯托克斯光子，以致更有可能通过受激发射，从其他斯托克斯光子中产生新的斯托克斯光子。在这种情况中，斯托克斯辐射的增长率正比于泵浦激光光子密度n_L和斯托克斯光子密度n_s。实际上，若令光纤轴为Oz，就可以用下列的微分方程表示该泵浦沿Oz轴传播时斯托克斯光子的增加速率：

式中，A为材料的常数。为了保证在受激开始时，使该过程能够从n_s=0的前端开始，第三个因子（n_s+1）中的“1”是非常必要的。由“1”代表的（单位体积内）单个光子是自发产生。

当然，很快会成为n_s>>1的情况，所以对于该类光纤的大部分情况，式（9.14）变为

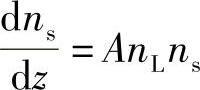
该式的解为

n_s=n_s（z₀）exp（An_Lz） （9.15a）(www.xing528.com)

式中，n_s（z₀）为z值（即z₀）处的斯托克斯密度值。其中，首先认为n_s>>1是成立的。

式（9.15a）更为习惯地表示为

I_s（z）=I_s（z₀）exp（gI_Lz） （9.15b）

式中，I_s为斯托克斯强度；I_L为泵浦强度；g为“拉曼增益”。由于g一定是正值（根据式（9.15a）中指数形式的结构），显然斯托克斯光子沿光纤轴的密度随距离成指数形式增大。此外，如果在泵浦的同时使一束具有斯托克斯频率的辐射光束入射到光纤中，则该光束会造成受激斯托克斯辐射，因而被此泵浦放大。在这种情况下有：

I_s（z）=I_s（0）exp（gI_Lz）

式中，I_s（0）为入射信号强度，因此构成了拉曼放大器。另外，由于没有相位匹配条件需要满足，所以泵浦和信号光束甚至可以在相反方向上传播，比较容易分离两种成分。

最后，如果在一段长距离光纤上可以充分地形成斯托克斯辐射，那么本身就可以作为一种泵浦以产生二级斯托克斯辐射。其频率是2ν_v，比原始的泵浦频率低。二级辐射可以产生第三级拉曼信号以此类推。到目前为止，在光纤中已经观察到5级斯托克斯辐射（见图9.12）。

图9.12　多级斯托克斯发射的光谱

这类斯托克斯拉曼光源是非常有用的多激光谱线光源，已经用于（在其他领域）单模光纤色散特性的测量。