拉曼散射：泵浦频率下的拉曼光谱，量子论的表述方式

当一束角频率为ω_L的强激光束入射到某种材料上，由该介质造成的散射辐射就包含高于和低于ω_L的频率。随着ω_L的变化，频谱会随ω_L移动（见图9.9）。换句话说，ω_L与由介质散射形成的频谱之间的差代表着该介质的特性。

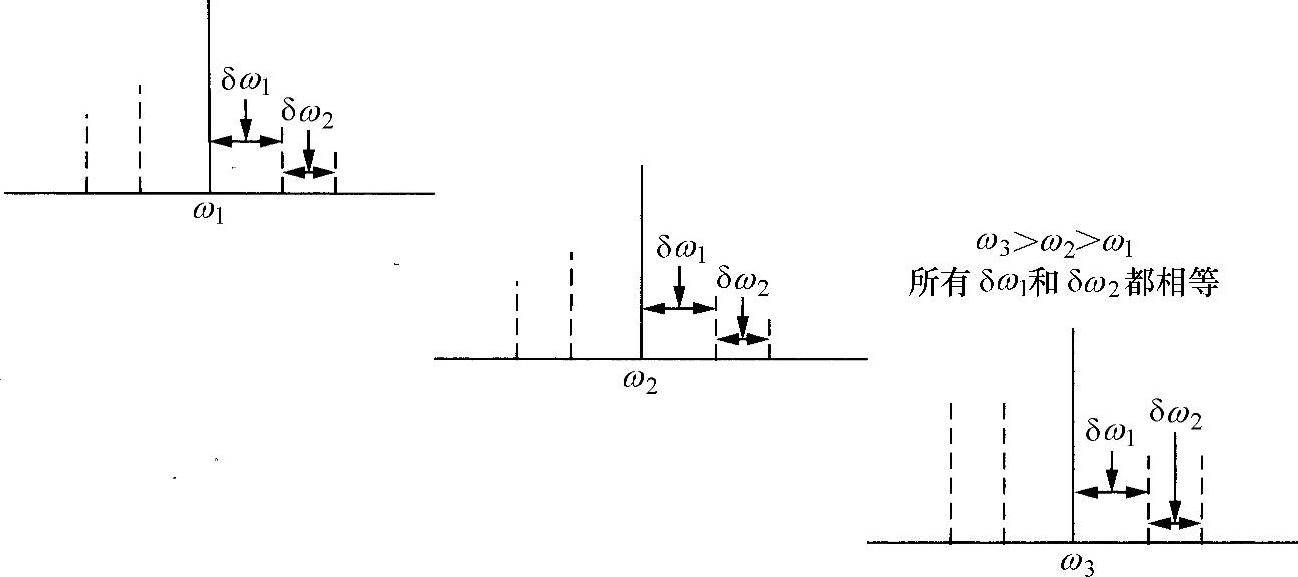
图9.9　不同泵浦频率下的拉曼光谱

这些差频恰好就是材料分子结构的振动模式和旋转模式，因此拉曼分光仪是一种用来检验该结构的非常有用的工具。若已知（定量给出）某振动频率ω_v，则有：

ω_s=ω_L-ω_v （9.11a）

式中，ω_s为斯托克斯（下移被减小的频率）频率，并且有：

ω_a=ω_L+ω_v （9.11b）

式中，ω_a为反斯托克斯频率（上移被增大的频率）。

首先，用经典理论（即非量子论）解释一种物理效应（如果可能）常常是非常有用的。因为该理论以人们比较习惯的方式提供了一种不全面的思维过程。更为重要的是，它给出了一种能比较好地表述其他物理量可能影响该效应的思想。对拉曼效应的经典解释可以参考分子的变体积磁化率的讨论。如本书4.2节所述，普通的体积磁化率定义为

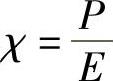
（为了方便，ε₀再次包含在χ中）。然而，由式（9.1）知道，P/E表示正负电荷能够被一个电场分开的难易程度，并非表示一个常数，它可以表示为电场的幂级数。基本理由是，进一步将电荷分开所需要的力在某种程度上取决于真实间隔。显然，如果讨论的是比较简单的正负点电荷+q和-q，那么其间的力就为

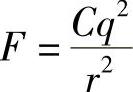
式中，C为个常数。所以，进一步分离所需要的力必须大于该数值，该力随1/r²变化。

在对振荡分子的经典阐述中，正负电荷中心之间的距离是按照正弦形式在一个平均值附近变化，具有小的振幅。所以，根据下式，可以希望体积磁化率χ也以同样频率按正弦变化：

χ=χ₀+χ′₀sinω_mt

式中，χ′₀<<χ₀。

如果是这种形式的分子振荡，并且具有下面表述方式的光学电场入射到该分子上：

E=E₀sinω_et

那么，电偏振就变为(www.xing528.com)

P=（χ₀+χ′₀sinω_mt）E₀sinω_et

即

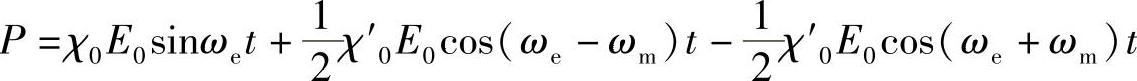
上列表达式的第一项代表分子的通常瑞利散射。这是主项，会产生与入射光波相同频率的散射光波。其他两项具有更小的值，给出P的下移和上移分量。由式（9.4）（和本书附录V）知道，随时间变化的电偏振会产生不同频率的辐射，所以漂移后的P会导致产生频率为ω_e-ω_m（斯托克斯）和频率为ω_e+ω_m（反斯托克斯）的拉曼辐射。

利用这种简单的经典方法定量表示下面内容是非常有用的：散射光波（或辐射）的光强度正比于入射光波强度，以及不同体积磁化率χ′₀的二次方。

然而，为了正确地量化拉曼效应，必须返回到量子论的表述方式。首先介绍式（9.11a）和式（9.11b）的一些结果。在式（9.11a）中，一个激光光子与原子相互作用，产生一个更低频率的斯托克斯光子。为了使能量守恒，必须满足下式：

hω_L=hω_s+hω_v

因此，在将分子激励到一种受激振动状态时，一定伴随着斯托克斯光子发射。但是，如果hω_L/2π并非对应着分子跃迁，会如何呢？为了回答这个问题，需要引用对虚能级的解释。一个分子可以存在于完全不同于系统实能级的虚能级中，能量为Δε，但存留时间仅为Δτ。其中，ΔεΔτ≈h（原文错印为ΔωΔτ。——译者注），h为量子常数。这是量子不确定原理的另一种表达形式。若是这种情况，就可以借助图9.10a所示解释斯托克斯发射：激光光子将分子从基态E₀提升到短期存留的虚态S₁，然后衰退到受激态。反斯托克斯的情况如图9.10b所示。对于这种情况，激光光子将已经受激的分子提升到更高的虚态S₂，然后衰退到基态。如此，用量子论观点对该现象就做了一个满意的解释。

图9.10　拉曼能级跃迁

当然，若是热平衡状态，受激态E₁的分子数与基态E₀的分子数之比由波耳兹曼因子给出：

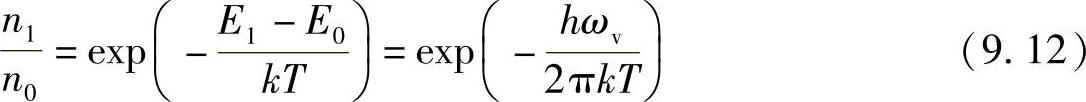
并且，它比1小许多。反斯托克斯辐射将发生在比斯托克斯辐射低许多的能级上，这是由于高频率时有较大的散射效率部分地被抵消。该效率随频率的四次方幂增大（参考附录V）。因此，当介质处于热平衡状态，反斯托克斯与斯托克斯辐射之比由下式给出：

式中

ω_v=ω_L-ω_s=ω_a-ω_L

与前面一样，应用同样的相位匹配条件。例如，为了有效地产生斯托克斯辐射，必须使激光光束的速度等于斯托克斯频率成分的速度。如果应用于晶体介质，如前所述，还要选择一个合适的方向，并且也必须这样安排。