四光子混合应用与相位匹配依赖性

在本章9.4节和9.5节已经看到，一定频率的两个光子可以在二次谐波形成过程及和频与差频形成时“混合”产生不同频率的光子，这些过程受到χ₂的调制。由本章9.6节知道，无定形介质中的电-光效应（克尔效应）由χ₃调制，用χ₃可以形成新的频率吗？如果在无定形硅介质中能够这样做，由于可以使用高强度（光源）及长距离光纤，所以很有可能实现这些过程。前面章节讨论的两个光子的混合过程是以式（9.1）中第二项场的二次方项中两个场的混合为基础，即χ₂E²，就是以两个光子为基础。若是利用第三项χ₃E³中的χ₃，自然希望包含三个光子。

现在讨论频率为ω_p、ω_s和ω_a的三种光波，并进一步假设（原因不久就会清楚），其间有下面关系：

2ω_p=ω_s+ω_a （9.10）

（注意，此处涉及4个光子）

很清楚，在该条件下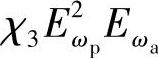，项将产生下面频率：

2ω_p-ω_a=ω_s

而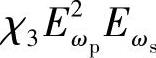项产生以下频率：

2ω_p-ω_s=ω_a

因此，借助ω_p和χ₃，ω_s和ω_a可以彼此连续形成。现在已经非常清楚，如果相位匹配（即ω_p、ω_s和ω_a的速度都相同），就完全可以出现这种现象。

有意思的是，利用高线性双折射（hi-bi见本书8.7节）光纤就能够实现。记住，这类光纤中两种线偏振本征模具有不同速度。另外，还要考虑材料和波导的色散。结果是，如果相对于色散特性正确地选择“泵浦”频率ω_p，并开始作为线性偏振波，那么偏振方向与光纤的慢轴一致。类似晶体中形成二次谐波的情况（见本章9.4节），则在其他偏振本征模（快轴）中的速度差及光纤（材料和波导）中的色散相组合，就允许ω_p仍在慢轴情况下使另两个频率ω_s和ω_a在快轴模式中具有相同速度，同时也满足式（9.10）。ω_s称为“斯托克斯（Stokes）频率”。当ω_a>ω_s时，ω_a称为“反斯托克斯频率”。该过程显然包括四个光子（ω_p，ω_p，ω_a，ω_s），因此命名为四光子混合（Four-Photon Mixing FPM）（很明显，有时也称为“三波混合”）。(www.xing528.com)

该过程类似于微波中的参量下反转，用于产生称为“信号”的向下反转频率ω_s和（不希望有的）称为“闲频”的向上反转频率ω_a。在高双折射光纤中产生的光学四光子混合频谱如图9.7所示。

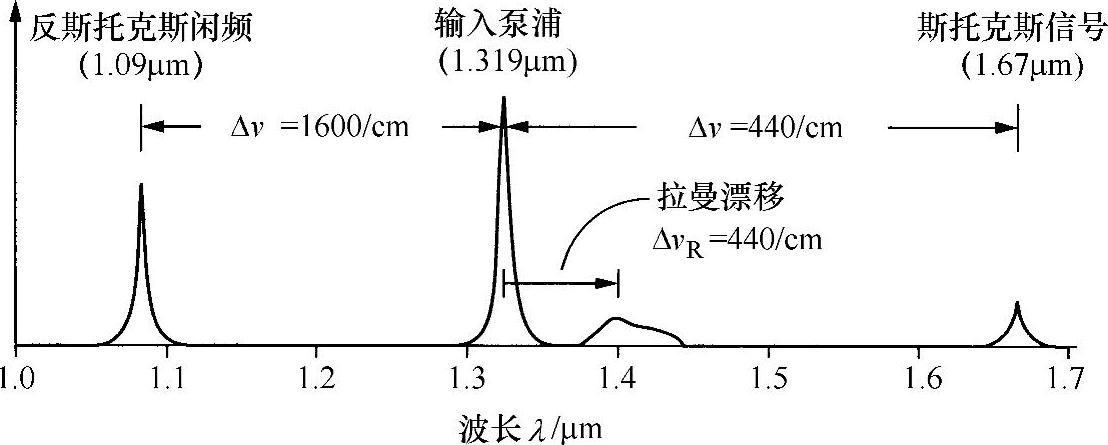
图9.7　高双折射光纤中四光子混合频谱

四光子混合有许多应用。特别值得一提的用途是光学放大器。如果注入一个频率为ω_p的泵浦，会使ω_s或ω_a处的注入信号获得增益（在过程的正交偏振方向）。通过同时在ω_s和ω_a（原文将后者也错印为ω_s。——译者注）处注入信号，之后改变其相对相位就可以控制增益。该泵浦会向更接近于相位匹配的分量提供更多增益（见图9.8）。

另外一种用途是确定高双折射光纤中何处是快轴，何处为慢轴。利用其他方法做这种确定相当困难，只有泵浦注入慢轴时，才会出现FPM。通过精确测量频率ω_a和ω_s，可以追踪双折射的变化。这意味着，在光纤中有希望应用这种技术感知影响双折射的外部扰动（如温度，压力）。

最后，也可能不希望存有四光子混合效应。在光纤通信中，由于多变的双折射效应产生非输入信号频率，所以可能会导致多通道系统（即波分复用（Wave-length-Division-Multiplexed，WDM）系统）串扰。

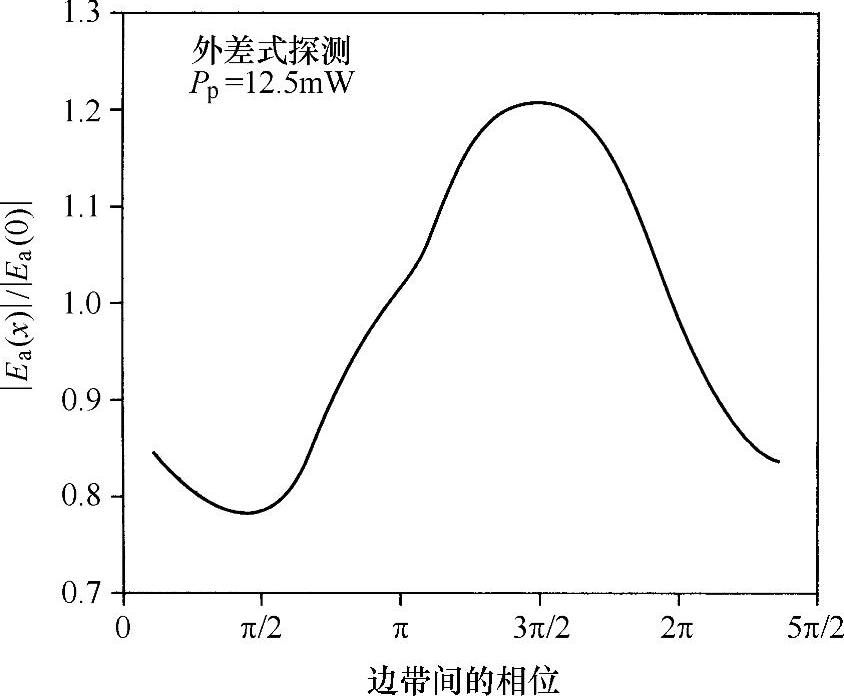
图9.8　四光子混合中参量增益对相位匹配的依赖性^[8]