自相位调制-光子学设计基础第2版

折射率与光强度有关（这种现象）清楚地隐含着下面意思：波的相位是在非线性介质中传播。因此有：

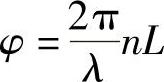
若n=n₀+n₂I，则

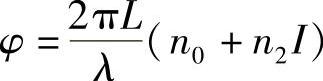
假设，光强度是一个与时间有关的量I（t），可以得出结论：φ也是与时间相关的量，并且由于

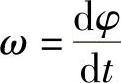
所以，频谱也会由于这种影响而改变，称为自相位调制（Self-Phase Modulation，SPM）。

在色散介质中，一种随时间变化的函数（即一种脉冲），其频谱变化会使该函数的形状发生变化。例如，在适当的环境条件下，可以使脉冲变宽或者变窄。为了说明这一点，现在讨论高斯脉冲（见图9.6a）。也就是说，高斯形状调制一种频率为ω₀的光学载体，新的瞬时频率为

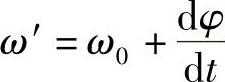
如果该脉冲是在Oz方向传播，则有：

则

(www.xing528.com)

在脉冲前沿，dI/dt>0，因此有：

ω′=ω-ω_I（t）

在脉冲后沿有：

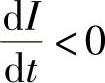
和

ω′=ω+ω_I（t）

现在，该脉冲已被线性调频（即脉冲范围内的频率是变化的）。图9.6b所示就是这种效应的例子。

假设，一个初始宽度为180ps的锁模氩离子激光器发出的脉冲沿着100m的光纤传播。由于自相位调制，频谱在传播过程中发生了变化。如图9.6c所示，当脉冲的初始峰值功率变化时，可以看到频谱如何变化。根据式（9.9a），峰值功率将导致峰值相位的变化，并表示出每种频谱的相位变化。可以看出，初始频谱Δφ=0恰恰是由于光学正弦曲线的调制（高斯脉冲的傅里叶光谱），并且随Δφ值增大，第一种效应就是变宽。当Δφ=1.5π时，该光谱被分成两个清晰的峰，对应着脉冲前后沿的频率漂移。此后，该脉冲发展为多峰值脉冲。

重要的是要认识到，并不一定需要改变脉冲包络线的形状，只需改变其中光学频率包含的形状即可。然而，如果脉冲穿过的介质是色散材料，脉冲形状将会改变。这是一种非常有意义的事情，将在本章9.9节讨论。

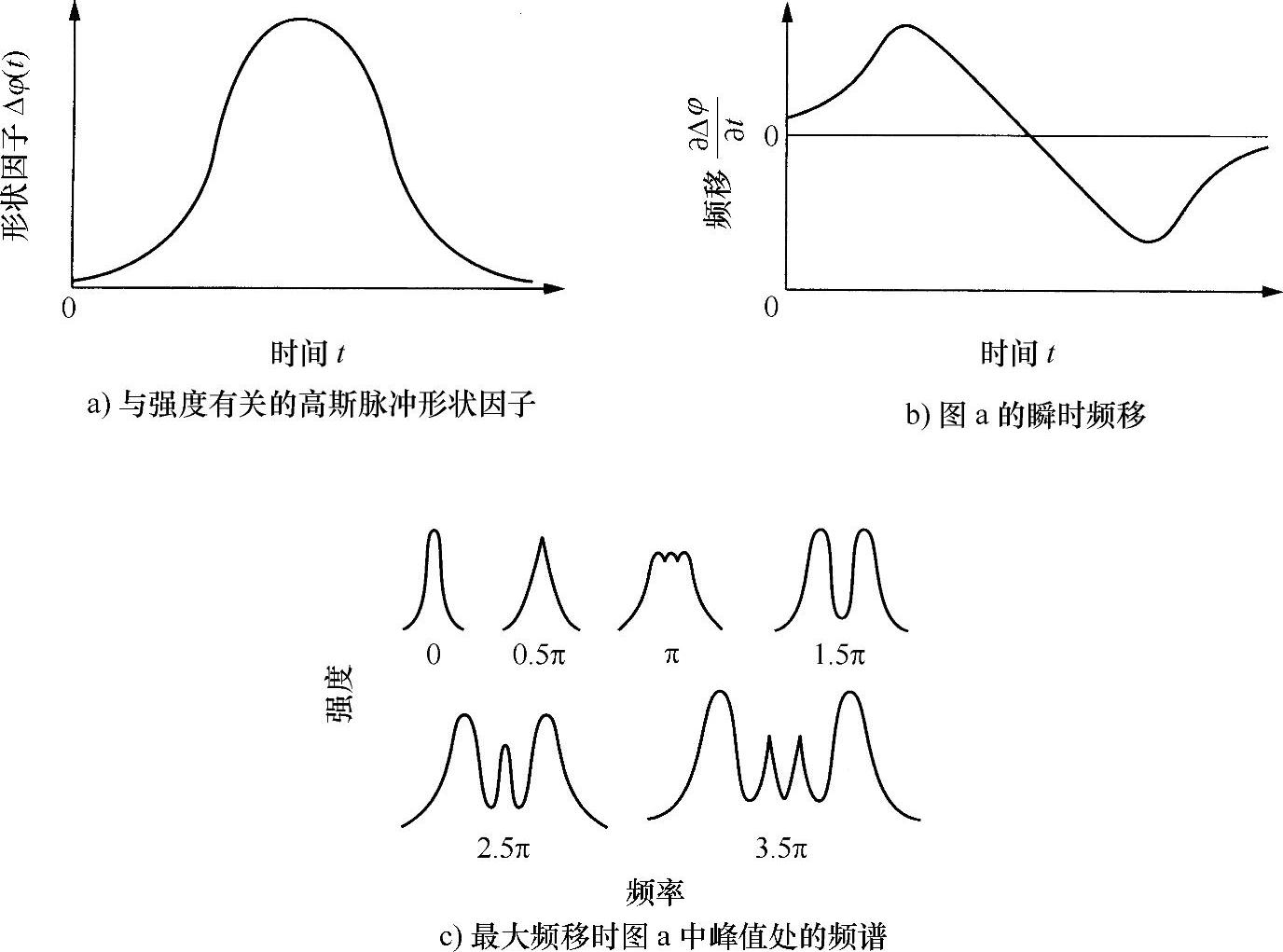
图9.6　对高斯脉冲的自相位调制^[6]