二次谐波发生和相位匹配

或许，一种介质非线性光学性质的最直接结果是基频第二次谐波的产生。为了从数学角度进行分析，假设一种光学介质的电偏振可以相当满意地用式（9.1）的前两项表述，即

P（E）=χ₁E+χ₂E² （9.3）

在继续分析之前，对式（9.3）有一点需要重点说明。

现在来看改变E的符号会有什么影响，场的两个值±E对应着两个P值，即

P（+E）=χ₁E+χ₂E²

P（-E）=-χ₁E+χ₂E²

显然，这两个量有不同的绝对值。如果介质是各向同性的（如制作光纤的无定形硅），在介质中没有方向性，E的符号（电场指向下或上）就没有影响，也就不会有任何能测量出的效应。实际上，不可能影响电偏振的值（当然，这是完全可测量出的值）。希望的是E的符号变化仅改变P的符号，而P的大小完全不变。也就是说，电子在相反方向移动同样的量，所有方向是等效的。显然，只有χ₂=0才能是这种情况。同样的观点应用于更高阶项。最终得出结论，所有无定形材料（各向同性）的偶阶项一定是零（即χ_2m=0），这是需要记住的一点。当然，该结论的必然结果是，为了保留偶数项，介质必须呈现各向异性，如必须是没有对称中心的晶体结构。由此还可以得出结论：式（9.3）就适用于这种介质。

假设，用下式表示进入这类晶体介质的光波电场：

E=E₀cosωt

代入式（9.3），得

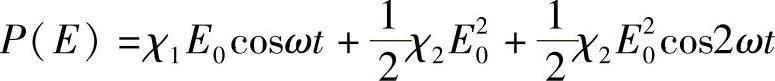
显然，最后一项是具有两倍初始频率的第二级谐波项。从根本上讲，其原因是由于晶体的非对称性，即一个方向比另一个方向更容易发生偏振出现一种“整流”作用。

现在，光波通过晶体的传播是将原始波附加到由其振荡偶极子感应产生的第二级子波上。正如本书4.2节所讨论的，用P表示这些振荡偶极矩。由于辐射功率正比于电荷的加速度，所以∂²P/∂t²产生e/m波，并且所有P对应的频率的波都将通过晶体传播。

假设，准备在长度为L的晶体内产生二次谐波。沿输入波光路任一点都会产生二次谐波分量。但由于晶体介质几乎都是色散材料，所以基频和二次谐波分量会以不同速度传播。一般来说，由基频产生的二次谐波分量的后续部分彼此间将不会同相，所以不会相长干涉。其效率取决于这些波之间的速度差。在本书3.10和8.7节处理高双折射光纤时遇到过类似现象。

对该过程的精确论述需要包括麦克斯韦（Maxwell）方程在内的运算，已经阐述在附录Ⅷ中。在此介绍一种完全符合物理学意义的半解析处理方法。

假设，晶体中沿光路在z与z+dz之间传播的基波（驱动波）振幅是ecos（ωt-kz）。根据式（9.1），会有一个电偏振分量（单位体积的偶极矩）χ₂e²cos²（ωt-kz），可以给出一个随时间变化的二次谐波项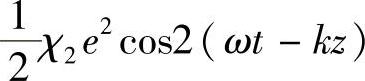。下面讨论介质中厚度为dz的一块单位截面平板（见图9.3）。

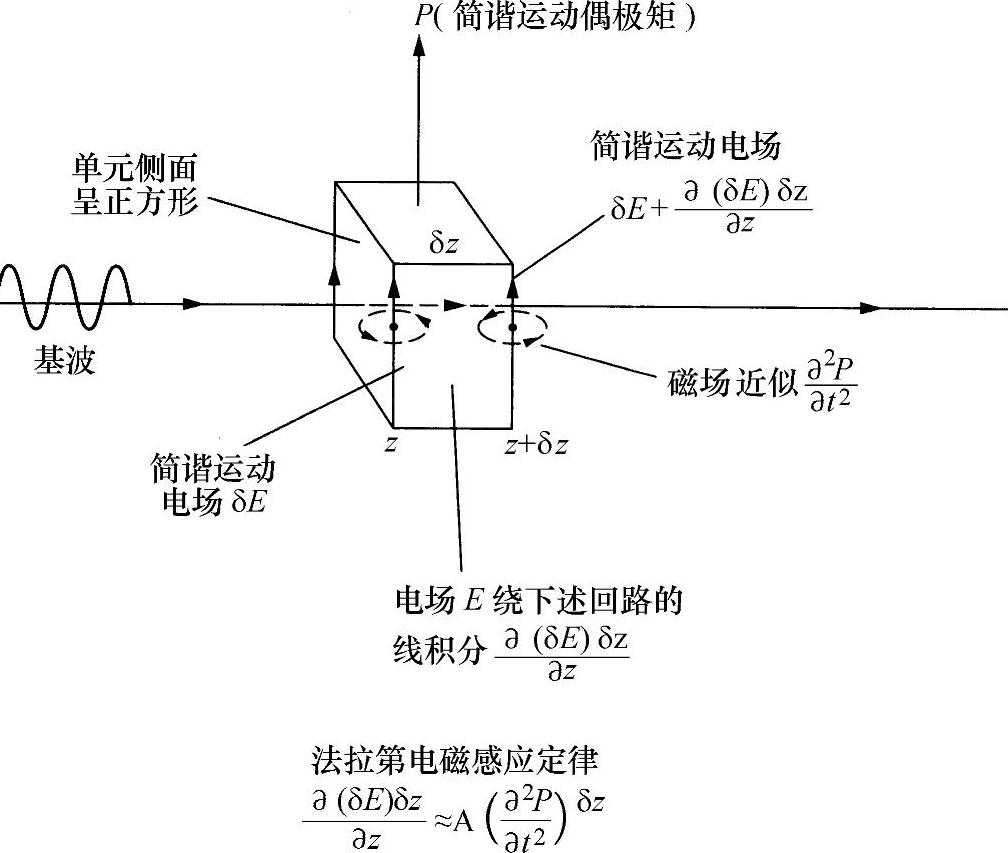
图9.3　沿基频光路产生二次谐波的无穷小单元示意图

这块平板的偶极矩为

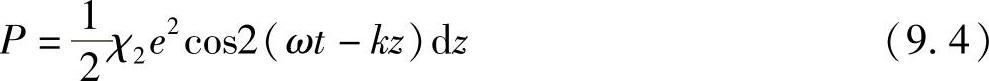
随时间变化的偶极矩表示电荷的移动，所以代表着电流。该电流会产生一个磁场。一个随时间变化的磁场（偶极距的二次微分∂²P/∂t²），在其穿过的回路中产生电压（法拉第电磁感应定律）。由图9.3可以看出，如果δE是由于改变薄板中偶极矩产生的二次谐波场的电分量，该电压就正比于∂（δE）/∂z，因此有：

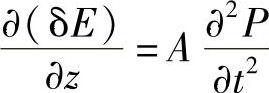
式中，A为常数。

由式（9.4），

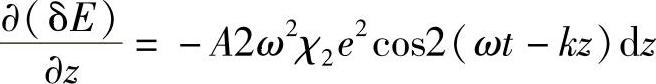
相对于z进行积分得到：

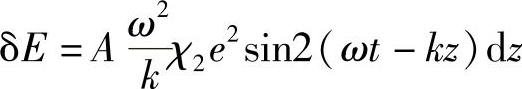
由于ω/k=c，则有：

δE=Acωχ₂e²sin2（ωt-kz）dz

这就是厚度为z和z+dz之间的平板产生的二次谐波电场元。但是，二次谐波分量现在以波数k_s传播（与频率ω处相比，频率2ω处有不同的折射率），当该分量传播一段距离L-z之后出射时就变为

∂E_L=Acωχ₂e²sin[2ωt-2kz-k_s（L-z）]dz

因此，在长度为L的晶体内产生的出射处的总电场振幅为

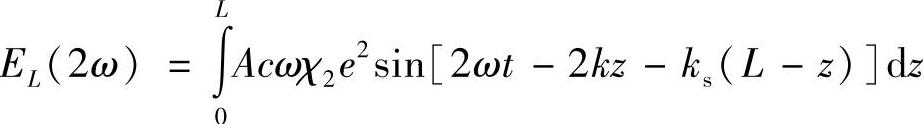
完成积分得

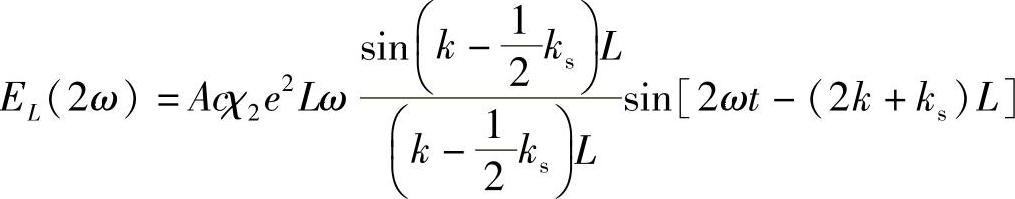
出射的二次谐波的强度正比于该振幅的二次方，即(www.xing528.com)

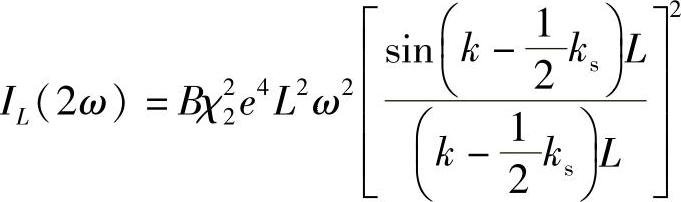
式中，B为另一个常数。基波的光强度正比于e²，所以二次谐波的光强度正比于基波光强度的二次方，即

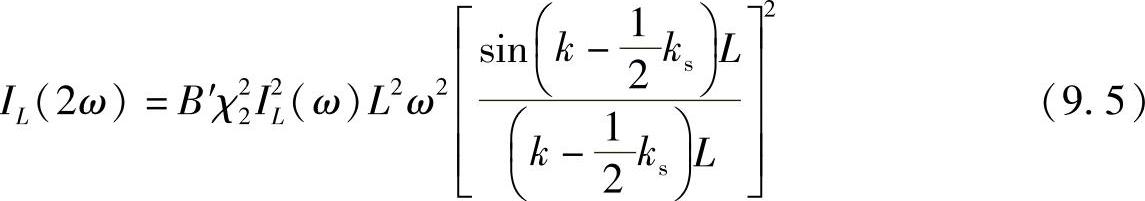
式中，B′为另外的常数。（附录Ⅷ精确地推导了式（9.5））由此，二次谐波产生过程的效率η_SHG可以定义为

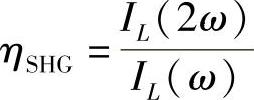
注意到，η_SHG随基频和晶体长度的平方变化，并随基频功率线性增大。

由式（9.5），很清楚，为了得到最大光强度，要求sinc²函数有最大值，就是说，

k_s=2k_f

这就是产生二次谐波的相位匹配条件。现在，基波和二次谐波的速度分别为

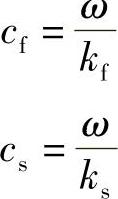
当k_s=2k_f时，两种速度是相等的，所以相位匹配条件等效于要求两种速度相等。这意味着在材料任何一点的基波都能产生相长干涉的二次谐波分量，所以这正是所期望的结果。在本书3.10节和8.7节，在处理高双折射光纤中偏振本征模间的耦合时，得出过同样结论。

一般，通过在晶体内特定方向选择光路，可以满足相位匹配条件。已经注意到，为了产生二次谐波，材料必须是各向异性的，因而呈现出双折射（见本书3.3节）。获得相位匹配的一种方法可以这样安排：材料色散产生的速度差抵消双折射产生的速度差。对具有正常色散的材料，两种本征模（寻常光线和非寻常光线）的折射率都随频率增大。现在，讨论特定例子石英，它是一种正的单轴晶体（见本书3.3节）。这意味着，非寻常光线的主折射率大于寻常光线的主折射率，即

n_e>n_o

由于石英也是正常色散，由此得出结论：

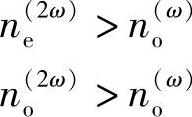
两种折射率椭球如图9.4a所示。由本书3.3节知道，晶体中任何给定方向“o”和“e”光线的折射率都可以根据满足下列条件的椭圆长轴和短轴给出：该椭圆平面垂直于给定方向、通过折射率椭球中心并与椭球表面相交。由该图（即图9.4a）所示可知，满足下面条件就可以确定一个方向^[1]：

n^（2ω）_o（θ_m）=n^（ω）_e（θ_m）

所以，只要下式成立，就可以出现倍频效应（Second-Harmonic Generation，SHG）相位匹配：

n^（2ω）_o<n^（ω）_e

对石英材料，上述结果在光谱范围内的确是对的。根据主折射率，由简单的三角法可以确定θ_m：

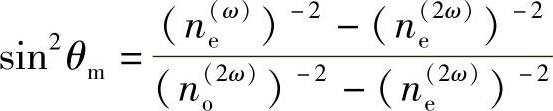
θ_m就是出现相位匹配的角度。在这种情况下如果出现倍频效应，则基频处的波一定相对于晶轴成θ_m入射，并且一定有“非寻常偏振”；在同样方向会出现二次谐波分量，还有“寻常偏振”（即两种波共线，但有正交的线偏振）。显然，对于其他晶体，可能有另外的晶体方向和偏振布局。

许多晶体都能够满足所需条件，但是由于石英有良好的强度、容易得到高光学质量的产品和获得高光学功率，所以是一种特别好的材料。

若输入的光沿所选择的轴传播，与通过晶体的其他光路相比，其转换效率（ω→2ω）有最大值（单位长度）。然而，必须使光束的发散度减至最小（以便大部分能量沿选择的方向传播），并确保温度不变（晶体双折射与温度有关）。

倍频效应的粒子图可以看作基频处两个光子的湮没及二级谐波频率处一个光子的形成。为了能量守恒，这对过程是必需的，即

2hν_f=h（2ν_f）=hν_s

因此，相位匹配条件等效于动量守恒。光子波数为k的动量为

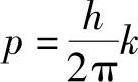
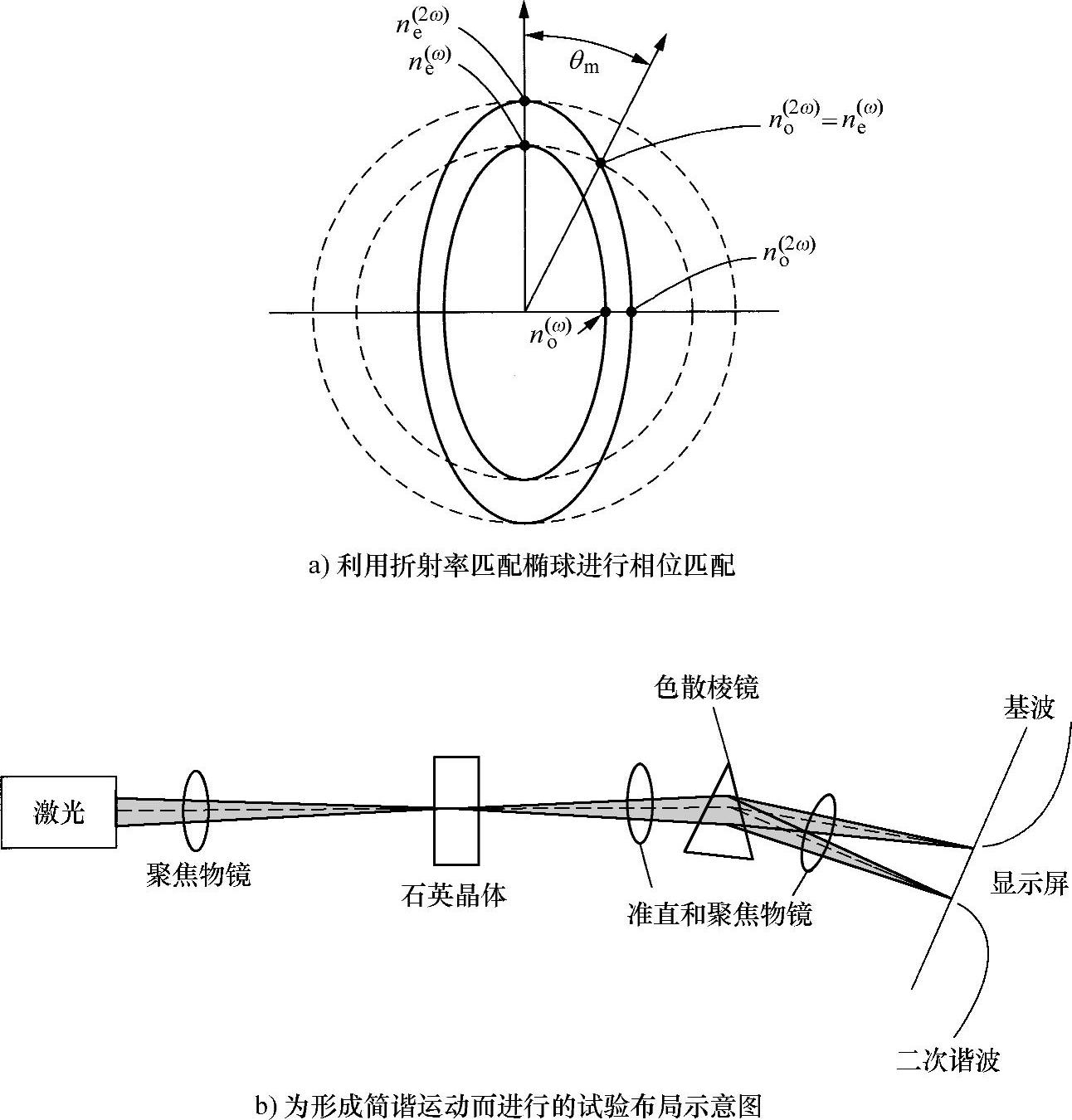
图9.4　石英中形成倍频效应的条件

因此，与处理波动一样，能量守恒要求：

k_s=2k_f

量子过程不再耗费多余的动量，并再次凸显可实现性，因此代表了粒子图中最大转换效率的条件。

倍频效应在实用方面的最重要之处在于，可以在高频下产生蓝光和紫外光激光。正如前面所述（见本书6.2.4.1节），从本质上说，此时的条件对受激作用并非有利。由式（9.5）注意到，该倍频效应的效率随基频的二次方增大，有助于产生高频。