保持偏振模式的光纤波导：偏振特性及应用

本书3.9节简要讨论了保持偏振模式的光纤波导。现在，更详细地进一步研究。

首先，重新研究具有应力感应双折射（两种折射率）的光纤。根据应力-光学效应，应力对于与其方向平行的线偏振光及相垂直的线偏振光会产生不同的折射率（见图8.24）。折射率差意味着两种偏振态间有速度差。正如已知的，这是波导的两种偏振本征模。速度差表明，除非该光纤受到专门扰动，否则入射到一种本征模中的线偏振光就被锁定在该偏振态内。其原因是，一般来说，由于两种分量之间有速度差，所以一种本征模随机耦合到另一种本征模上不是同相，因此很容易相消干涉。然而，如果一种耦合扰动（使其轴发生局部旋转的一种外加应力，见图8.24b）的空间周期等于两种本征模实现同相的距离，也可以出现耦合。那么，该距离是多少呢？假设，折射率差是Δn，在这种情况下，该量也称为双折射，用B表示。若波长是λ，则在距离b范围内由Δn产生的相位滞后为

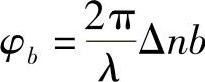
若两种本征值在光纤某给定点同相，那么只要满足下列条件，在传播一段距离b后也可以保持同相：

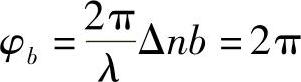
即

式中，b为“拍长度”，是双折射光纤特性的重要参数。注意到，该参数与光波波长成正比。显然，空间周期等于b的扰动总是将分量从一个本征值同相耦合到另一个本征值，从而发生相长干涉，是强耦合。对于任意扰动函数，其耦合取决于具有拍长度周期的傅里叶分量的振幅，光纤的拍长度越小，可能给出的扰动就越小，实际上包含有大振幅的傅里叶分量和小的周期。例如，为了在小于一个拍长度的距离上施加应力使其具有这种分量，需要对光纤增加一个重力。因此，具有小拍长度（即高双折射）的光学纤维将会非常好地保持既定的入射本征值，并且可以用于将线偏振光从一个位置转移到另一个位置。这种光纤称为“高双折射（high-birefrigence，hi-bi）”光纤，在各种应用中用作偏振控制。在某些应用中，有时也称为“保偏光纤”。一种典型hi-bi光纤在波长850nm时的拍长度约2mm。由式（8.13）得

Δn∝4.25×10^-4

其中，n₁≈n₂≈1.47，折射率差仅约0.03%，但足以提供很强的偏振特性。原因是，短光学波长可以传播非常长的光路，根据φ=（2π/λ）Δnl，相位影响迅速积累。

图8.24　保偏光纤中的光耦合

hi-bi光纤的偏振性质对各类外部扰动都很敏感，因此可以广泛应用于光纤传感器。本书第10章将介绍这方面的应用。

现在，讨论另外一种双折射光纤，即图8.25所示的椭圆芯光纤。在这种情况中，双折射是波导外形结构造成的结果，对波导作用原理的最新认识可以加深对该机理的理解（完整的数学描述相当复杂，见参考文献[6]）。一条光线以垂直于入射平面的线偏振态通过最大长度的路程。粗略地说，相长干涉的条件对应于主轴等于a的式（8.1b）。也就是，2akn₁cosθ+δ_s=mπ。

图8.25　椭圆芯光纤(www.xing528.com)

因此，可以确定对应于该长度和偏振态的θ和δ_s值，再依次根据这些参数确定一组ω/β色散曲线，类似图8.3所示。若是平行偏振，会有不同的曲线组。

对于通过最短长度b传播的光线，将有两组以上的曲线组。显然，由于a≠b，每一种线偏振态和其他四组曲线都不一样。不难理解，任意两个对应垂直态相组合都会形成一种模，根据两种平行态相组合得到的结果（见图8.25c），也可以得到不同组的ω/β曲线。若ω值一定（即光学频率一定），两种线偏振态的dω/dβ也不一样，并且有不同的群速，因而具有线双折射。这是椭圆对称性（两个线本征模的方向应当与椭圆轴的方向相对应）的自然结果。只有光线在长轴终端或短轴终端之间反射时，才能被限制在一个平面（包含波导轴和椭圆轴的平面）内。其他的所有光线都将与椭圆相交。

如果椭圆度不太高，模式偏离截止频率也不太远，可以看出这种情况^[6]下的双折射为

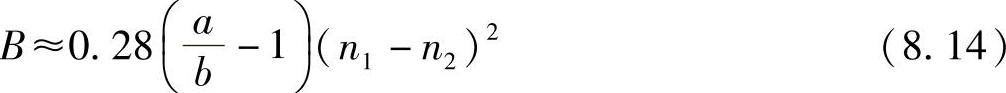
式中，n₁为芯的折射率；n₂为包绕层的折射率。

这些光纤的a/b值范围通常在1.2左右。由于必须保持下面的单模条件，所以n₁-n₂的值受到限制。

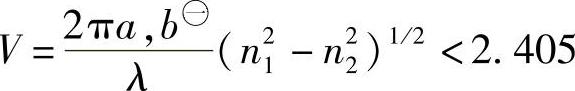
㊀　“a，b”表示a或者b。——译者注

实际上，要使（n²₁-n²₂）尽可能地高，通过减小椭圆尺寸a和b以保持单模条件成立。然而，同时会造成下面的事实：使芯的面积减小，因而造成与光源和其他部分的对准相当困难。另外的问题是，如果使芯材料有更多掺杂而增大n₁，就会使光纤的衰减增大。

若芯和包绕层（通常芯材料中掺杂锗）之间的折射率差为4%，那么式（8.13）表明，这类光纤在波长850nm处的拍长度为1mm数量级。

椭圆形芯高双折射光纤，在应力引发的变化范围内具有的一个重要优点，是具有较低的双折射温度系数（约5倍）。原因是其产生的结果是由几何形状引起，与应力引起双折射一样，应变光学系数与温度无关。

正如本书3.9节讨论的，光纤双折射对光通信是一个缺点，会引入另一种形式的色散。因此，带宽受到限制，除非采取措施将其减小到可接受的程度。例如，在光纤抽丝过程中使坯件旋转以消除波导截面的各向异性。

此外，线性双折射并不是出现的惟一双折射形式（见本书3.9节讨论的内容）。波导可以具有任何椭圆形式的偏振本征模，包括特殊情况下的线和圆偏振模。（根据定义）这些本征模具有不同速度，因此通常在波导中都用椭圆双折射。由于本征模存在速度差，所以，这种波导对任意输入的偏振态影响可以通过将输入态分解为两个本征模分量（总是可能的）；在输出时重新将它们组合起来，使其相对相位等于波导插入的相位，从而用解析方法确定。实际上，线性和圆双折射是最经常遇到的类型，在经济上也非常合算。

对其偏振态的控制，可以进一步加强对波导传播光的方向和位置的控制。在光子学中，有许多利用这种控制的实际例子，其中一些将在本书第10章讨论。