波导色散-光子学设计基础

在本章8.2节和8.4节分别讨论平面波导和柱面波导时已经知道，无论何种模式，尤其是最低阶模式，ω与β（见图8.3和图8.8）之间都是非线性关系。当然，这种最低阶模只能在单模光纤中传播。这种非线性源自波导边界条件必须满足不同光学频率的要求，特别要遵从下面的事实：光线入射到边界上的角度随频率变化，随之在全内反射时有不同的相位变化，后者是入射角的复杂函数（见本书2.6节）

根据上一节（本章8.6.2.2节）及本书4.3节对脉冲扩展的讨论，注意到根据式（4.11），在传播一段距离L后，对于其能量已经扩展为光谱宽度是δω的脉冲，到达的时间间隔为

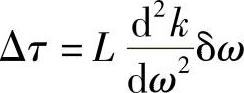
显然，在目前这种情况下，k一定被制导的波数β替代，得

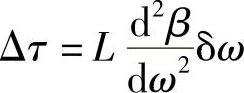
若有波导色散，对于一定的模数，特别是最低单模情况，就可以根据β与ω曲线（色散曲线）计算Δτ。

产生这种形式色散的物理原因有两个：第一，随着某种模式的频率变化，边界处入射角随之变化，就意味着光线沿波导以不同速度传播（实际上，速度随sinθ变化）；第二，随着频率和边界上的角度变化，正如本书2.6节所讨论，损耗波对第二种介质（包绕层）的穿透能力也在变化，因此制导通道与外层介质中损耗波场的相对功率也随频率变化。由于两种介质的折射率不同，所以导致制导后光波折射率随频率发生变化就不奇怪了。(www.xing528.com)

对于柱面波导^[5]，已经得到最低阶模的芯和包绕层的功率比，一阶近似表达式为

式中

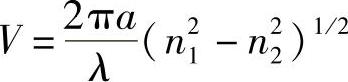
随着波长λ增大，芯中的能量逐渐转移到包绕层中。从物理学观点，已经定性地得到证实：随着λ增大，正如式（8.2a）所要求，入射角θ减小（即光线与轴的夹角更大）。由于入射角θ减小，损耗波的穿透能力增大（见本书2.6节）。因此，在波长较长（较低的β）时，它对包绕层介质有较大的影响，并且波导折射率倾向于使包绕层折射率n₂（见图8.18a）。显然，当波长变短，所有这些结论就是相反的。尤其是，波长变短会使折射率倾向于芯的折射率。对于非常短的波长，若的确比芯的直径小许多，则对于一级近似，该波就不会感知这两种介质间存有边界，仿佛在折射率为n₁的未受任何约束的芯介质中传播。

实际上，波导色散非常有用，原因是可以将它设计成与材料色散相反。波导色散与芯的几何形状有关（见式（8.12））。通过适当地选择外形，能够将光纤的色散最小值从材料确定的色散值移到另外方便的（但相当接近）波长处（见图8.18b）。以这种方式调整过的光纤称为“色散转移光纤”。并且，利用这种方法可以将色散最小值的波长从其“无约束值”1.28μm处，移到如1.55μm处，从而使吸收造成的衰减降低。利用这类光纤可以安装几百公里长、不可重复的干线通信系统。