光子学设计基础：材料色散解析

在本书4.3节曾经介绍过材料色散的一些细节，正如当时所述，由于原子谐振的结构，使光学材料的折射率随波长变化。

注意到，折射率随波长的变化形成不同于相速的群速，由下式表示：

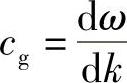
其中各变量满足下面关系式：

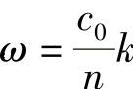
式中，n为材料的折射率，所以上式可以转换为

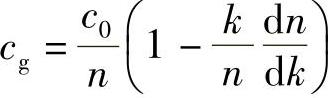
式中，c_g为光能量的传播速度。

显然，在光源光谱范围内，c_g不再是一个常数，除非dn/dk在该范围内是一个常数（也就是说，除非n是波长的线性函数），否则光源光谱的不同部分将以不同的速度传播。在其他效应中，这将使光学脉冲加宽。

群速为c_g，能量传输距离为L时所花费的时间为

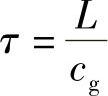
因此，一个宽度为δω的光源光谱的时间范围为

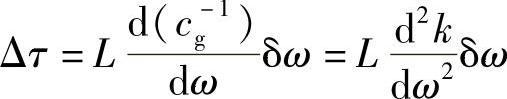
k=2π/λ=nω/c₀，所以也可以表示为

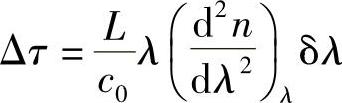(www.xing528.com)

式中，（d²n/dλ²）λ是（d²n/dλ²）在波长λ时的值。在此注意到，B≈1/Δτ，所以有：

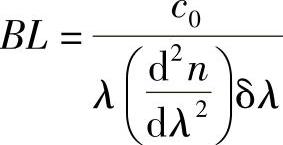
若光源和材料一定，该式是个常数。

为了使带宽与距离的乘积有最大值，d²n/dλ²、λ和δλ要尽可能小。很明显，（λ/c₀）（d²n/dλ²）（在波长λ处）表示材料特性，硅材料的该特性随λ的变化如图8.17所示。

由该图看出，在波长1.28μm处d²n/dλ²=0。

由此得出结论：这是硅材料光纤中具有最大带宽的最佳波长。特别幸运的是，该波长对应着硅材料吸收光谱中的最小值（见图8.13），因此在此波长下还有低的衰减。上述两个因素的综合考虑导致了20世纪80年代单模光纤通信技术的快速发展。

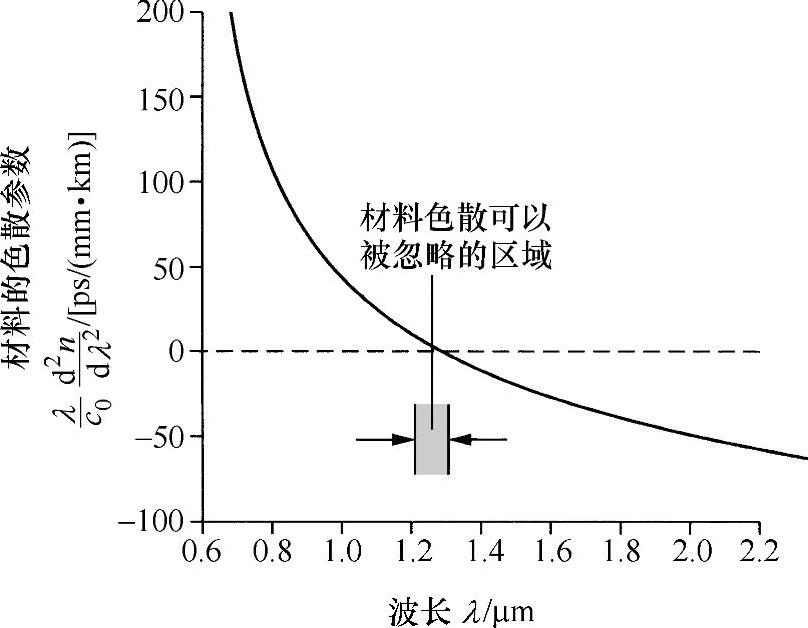
图8.17　硅材料的色散“零”

为了充分利用该波长下具有最大带宽的优点，还必须使光源的光谱带宽δλ最小。此项要求已经导致研发具有较高功率（约100nW）的窄带（约0.1nm）半导体激光光源。最近，已经研发出光纤激光器。

当然，在光源的整个带宽范围内，d²n/dλ²并不是零。能够达到的最佳状态是保证在光谱中心λ₀或附近为零。

将一些典型的数据代入公式，可以更深刻地感受其实用性。

假设，光源是波长范围约1nm的半导体激光器。由图8.17所示可以看出，在零点（1.28μm）附近1nm范围内的平均材料色散约为3ps/（nm·km）。

因此，Δτ≈3×10^-12/km，或者BL≈330Gb·km/s。

例如，线路长度为100km，则带宽是3.3Gb/s。这是一个非常期望的带宽，但是在这种距离下有希望做得更好些。最明显的改进方法是进一步将光源的光谱带宽降低到约0.1nm，在同样的距离范围内就有可能得到33Gb/s的带宽。然而，不要满足于此，与单模光纤相关的还有另外的色散源，就是波导色散。下面就讨论这方面的内容。