光子学设计基础第2版：模式色散攻略

本章8.5节简要介绍了模式色散，该色散只存在于多模光纤中。其原因是光纤模式具有不同速度，并不是材料色散而是光纤结构所致。光学能量入射到光纤内，并且进入光纤的多个模式，或许所有模式内。显然，模式色散的影响将取决于传播的能量在可能的模式中如何分布。并且分布沿光纤是变化的，要根据局部条件（即弯曲、接缝等），能量重新分配。为了对其数量级有所认识，很容易计算出在一个已知的距离范围内光纤最快和最慢模式间传播时间的差别。

最快模式是顺着光纤沿轴线（几乎是）的直线传播的（见图8.15）。中心介质中没有发生反射，速度是c₀/n₁。

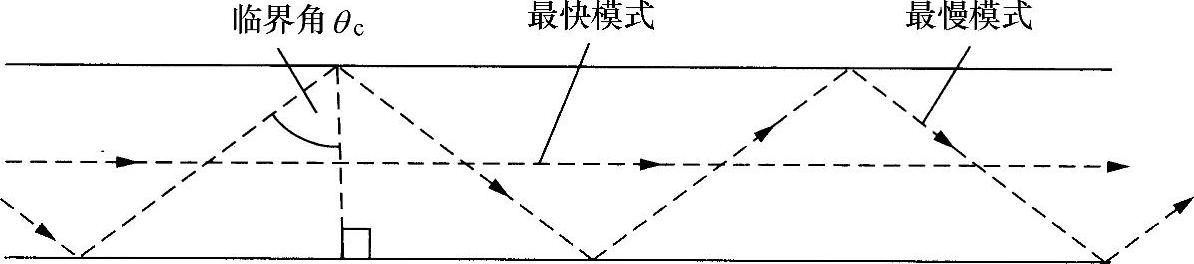
图8.15　模式色散

最慢模式是以全内反射角入射到芯/包绕层边界上的光线代表的传播（对更大角度，该光线将不再受到制导）。显然，这条光线是以速度（c₀/n₁）sinθ_c传播（见图8.15）。其中，θ_c是临界角。

由于：

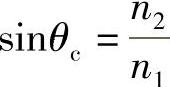
很容易看出，沿光纤长度为L传播的两种时间为

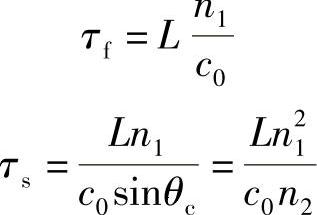
因此

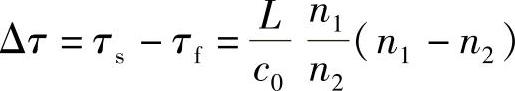
由于

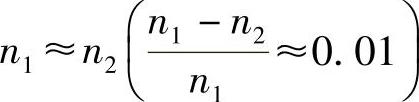
所以

式中，Δn为芯与包绕层间的折射率差。很明显，式（8.11）是一般式（8.10）的特例，因为由式（8.10）有：

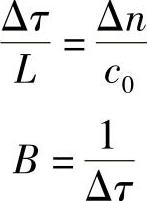
因此

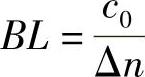
对于某已知光纤，等式右侧是个常数。一般地，若折射率差约为0.01，则有：(www.xing528.com)

BL=3×10¹⁰Hz·m=30MHz·km

对这种光纤，在1km距离内只有30MHz的适用带宽，若10km距离则仅有3MHz带宽等。显然，多模光纤的带宽容量严重地受到限制。

将B与一个光源能够入射到光纤内的光功率相联系是非常有意义的。根据本章8.5节内容，其数值孔径为

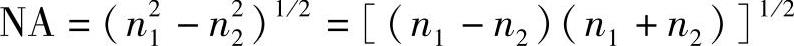
或

（NA）²=（Δn）（2n₁）

由于

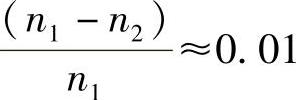
代替式（8.11）中的Δn，得

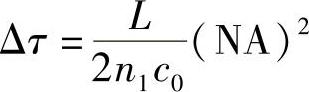
NA是光纤接受光源发射光难易程度的一种计量。由图8.16所示可以看出，接受立体角就是π（NA）²。因此，（NA）²的值越大，入射的光功率就越大。假设，被接收信号的噪声与光纤长度无关（几乎所有噪声都是接受装置产生的发射噪声和热噪声，所以这是一个合理假设），则可以得出结论：探测到的信噪比（SNR）正比于入射功率（对于一定的光纤长度），因此也正比于（NA）²，即

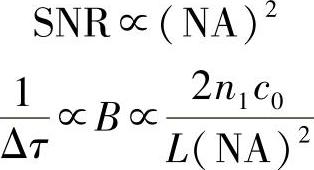
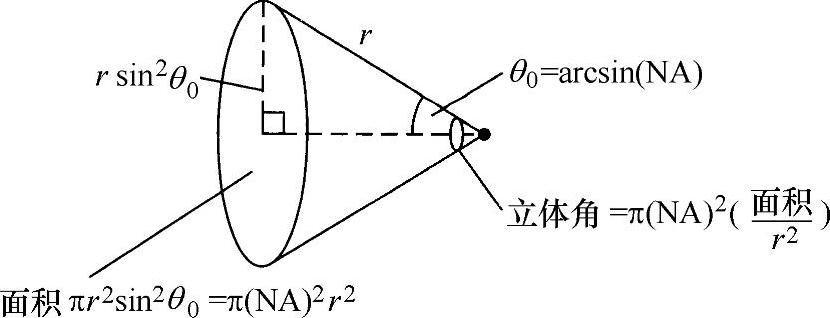
图8.16　光纤接受光的立体角示意图

和

SNR×B∝2n₁c₀/L

如果光纤长度一定，则SNR和带宽的乘积也是一个常数。增大（例如）数值孔径就可以增大进入光纤的功率，但以减小带宽为代价，原因是较大的数值孔径会增大模式色散。一般来说，这种关系在通信系统中是正确的，特别适合多模光纤线路。这些关系可以描述光纤通信系统设计师必须面对的那些折中类型。为了使多模色散减至最小，而使给定长度光纤的带宽最大，显然必须使模数减到最少。可能达到的最小绝对数是1，即一种单模光纤。单模光纤是光纤通信中优先选择的介质，现在只有相当短的距离（<1km）才使用多模光纤线路。

然而，在单模光纤中，其他色散光源显得十分重要。在多模光纤中，这些特征受到模式色散的抑制没有凸显出来。当消除模式色散后，其他色散效应就会限制通信系统的带宽。现在就讨论其他效应。