光学纤维设计：横向谐振条件和梯度折射率光纤

当然，柱形结构与光学纤维有直接联系，光学纤维正是一直讨论的结构形状，对于光学纤维有：

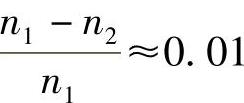
所以，弱波导近似表达式是成立的。图8.9给出了一些低阶LP模式的强度分布及对应于偏振和方位整数为1的值。有两种可能的线偏振光纤模式，若是柱形结构，那么“单模条件”（对于平面情况，类似于式（8.8））有下面形式：

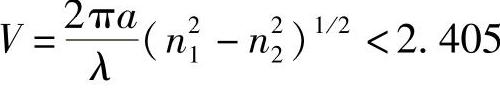
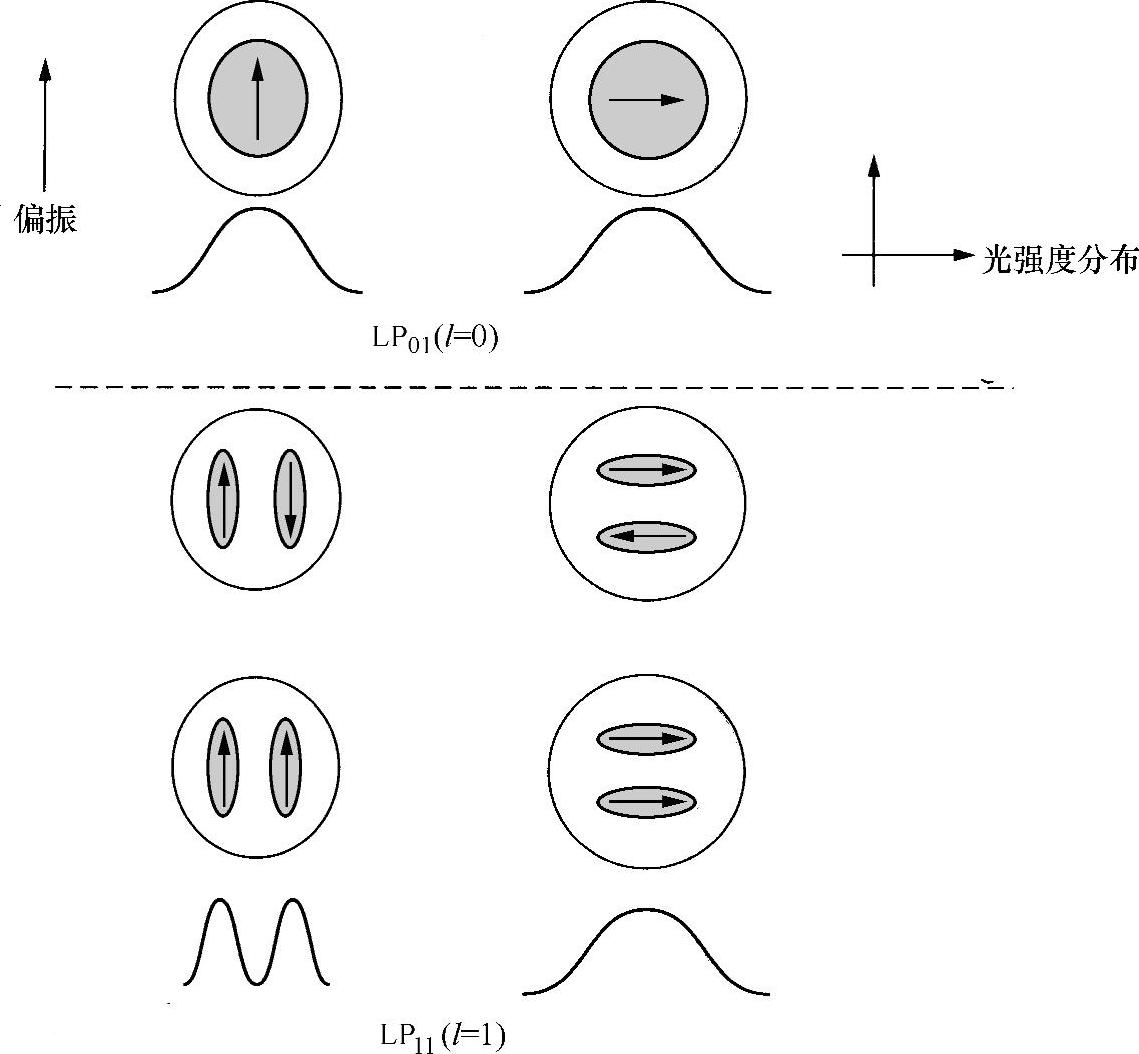
图8.9　柱形波导的一些低阶模式

数字2.405是根据最低阶贝塞尔函数J₀在第一个零值时得到的（见图7.21）。在几何光学领域，可以看到采用光纤设计方法所具有的一些重要和便于应用的性质。

首先讨论光线进入光纤的问题。如图8.10a所示，光线以角θ₀入射到光纤的前端面，折射后的角度是θ₁，有：

n₀sinθ₀=n₁sinθ₁

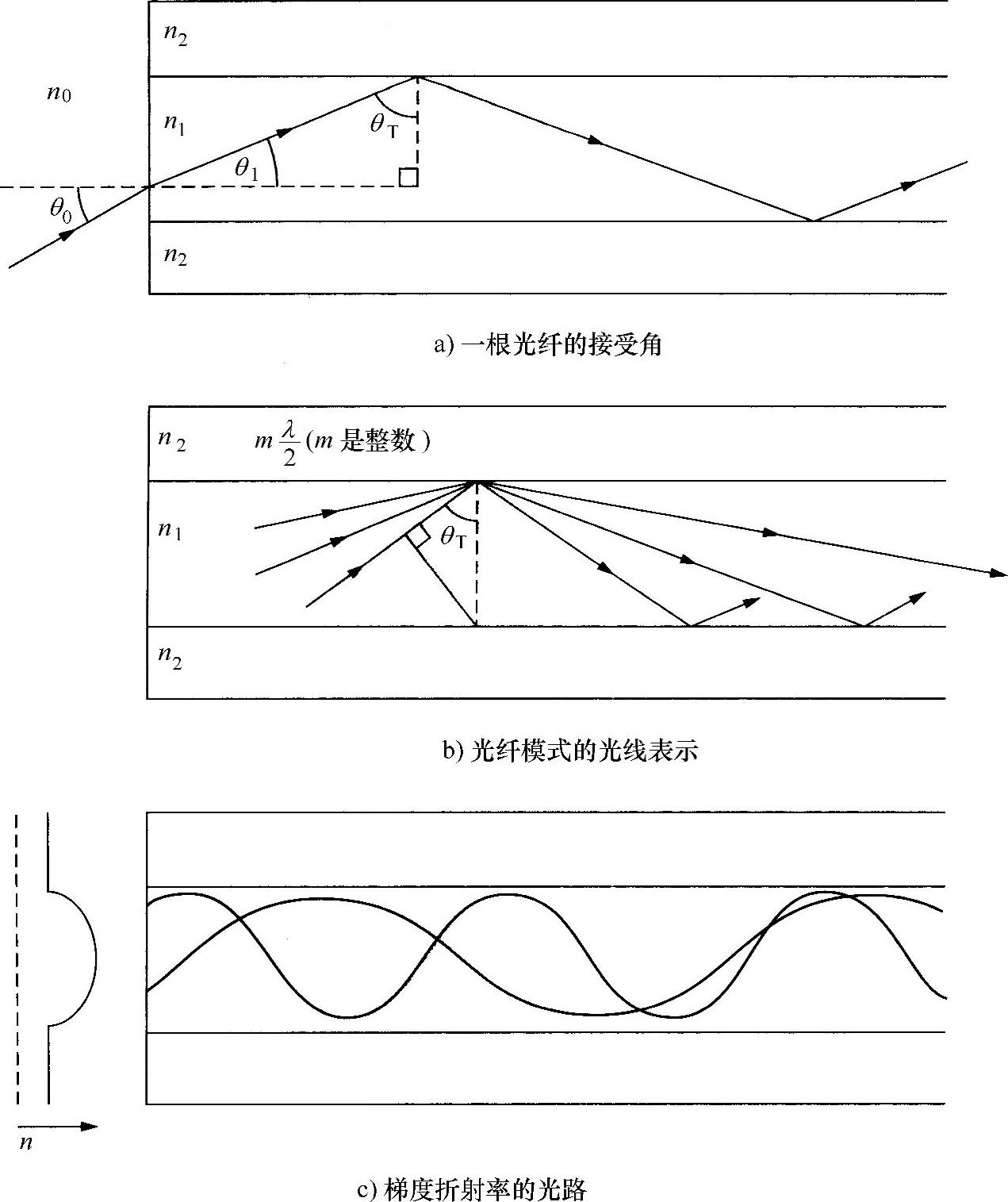
图8.10　光线在光纤中的传播(www.xing528.com)

式中，n₀和n₁分别为空气和光纤芯材料的折射率。为了得到全内反射，当光线以θ_T角度入射到芯/包绕层界面上，必须满足条件sinθ_T>n₂/n₁。其中，n₂为包绕层的折射率。

由于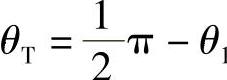，所以上述不等式等效于

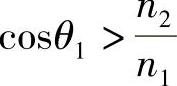
根据上面的Snell定律表达式得

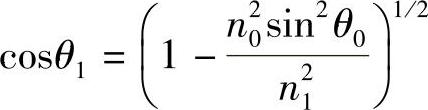
或

n₀sinθ₀<（n²₁-n²₂）^1/2

该不等式右侧的量称为光纤的数值孔径（Numerical Aperture，NA），是“接受”光锥的技术要求，也是半角为θ₀的顶锥。显然，为了有大的接受角，必须保证光纤芯与包绕层之间有大的折射率差，对于标准光纤，θ₀≈10°。

满足横向谐振条件（符合全内反射条件）的反射角离散值可以用图8.10b所示的光线传播表示。显然，对于大量的容许光线（即模式），全内反射角要大。这意味着有大的数值孔径。然而，从几何光学出发，这些光线将沿着波导以与反射角有关的速度传播，角度越小，速度也越小。如果入射的光能量是在多个模数间分布，由于不同速度会使能量有用部分到达光纤远端的时间发生变化，导致大数值孔径有大的“模态色散”，这是不希望出现的。例如，在通信应用中，这会导致对通信带宽的限制。在数字系统中，不允许将一个脉冲前后分成多个脉冲。对于最大带宽，只允许有一个模式，因此需要小的数值孔径。在良好的信号质量（大的NA）和大的信号带宽（小NA）之间就要折中平衡。在本章8.6节，将重新讨论该课题。

企图获得较好平衡位置的一种光纤设计如图8.10c所示，这种光纤称为梯度折射率（Graded Index，GI）光纤。图中给出了光纤芯折射率轮廓曲线，从轴上的峰值开始呈抛物线形式（近似地）下降。这种轮廓有效地组成了一个连续的凸透镜，允许有大的接受角，而将允许的模式数目限制到较小值。梯度折射率光纤广泛应用于短距和中距离通信系统中。然而，对中继系统，总是采用单模光纤，从而保证完全没有模式色散，也就消除了对带宽的限制。与多模光纤相比，单模光纤的通信带宽要高出一个数量级，但也不是毫无问题。现在讨论光纤以相干方式在通信方面的应用。