柱形波导的设计和解析表达式

现在讨论图8.6所示的柱形电介质（波导）结构。这是一种光学纤维形状，中心区域称为“芯”，外层区域称为“覆层”。在这种情况下，正如电介质薄片一样，遵从于同样的基本原理，但圆形而非平面对称性使数学分析复杂化。为了方便起见，使用图8.6定义的柱坐标（r，φ和z）。这就可以以下面形式表示电介质结构的麦克斯韦（Maxwell）方程（见附录Ⅰ）：

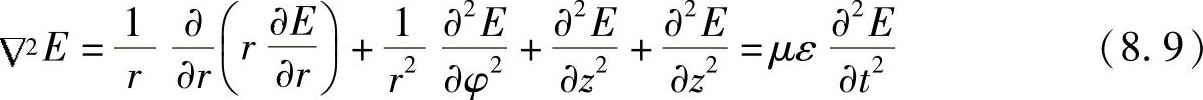
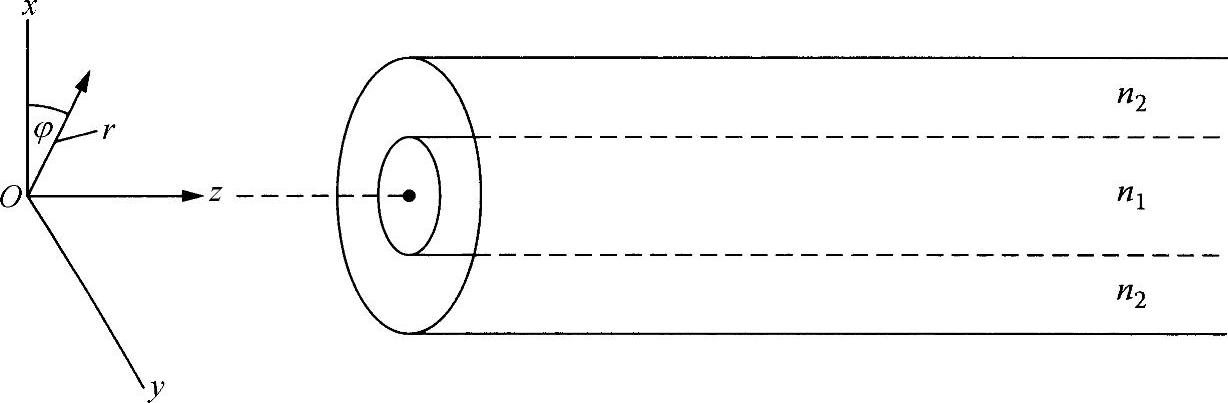
图8.6　柱形波导结构

如果尝试求解E的一个解，其中所有变量都是可分离的，则可以写为

E=E_r（r）Eφ（φ）E_z（z）E_t（t）

并且，根据物理学理论，可以立刻写出下面形式：

E_z（z）E_t（t）=exp[i（βz-ωt）]

换句话说，该波沿柱体轴线以波数β和角频率ω传播。从而可以得出结论，其（相位）沿轴的传播速度为

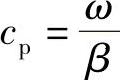
将这些表达式代入波动方程式，即式（8.9）中，就可以写成下面形式：

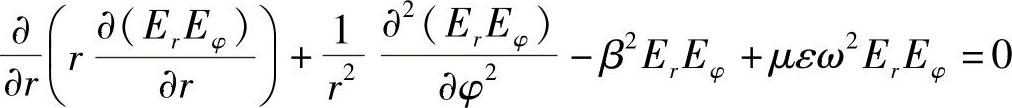
如果E_φ采用下面形式的周期函数：

E_φ=exp（±ilφ）

式中，l为整数，可以进一步将该公式简化为

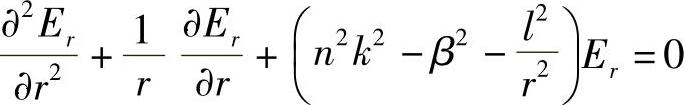
这是贝塞尔公式的一种形式，其解也是贝塞尔函数（参阅较高级的数学教材，即参考文献[2]）。如果利用与前面讨论平面波导时相同的置换方法：

n²₁k₂-β₂=q²(www.xing528.com)

β²-n²₂k₂=p²

若r≤a（芯），可以确定：

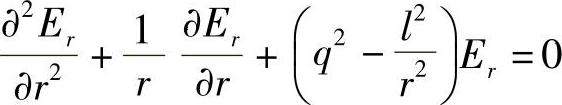
若r>a（包绕层），有：

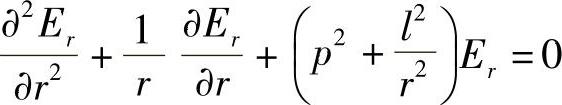
这些公式的解如下（见图8.7a）：

E_r=E_cJ_l（qr）　r≤a

E_r=E_clK_l（pr）　r>a

式中，J_l为一类贝塞尔函数；K_l为二类“变型贝塞尔函数”（有时，称为“变型汉克尔函数”）。显然，这两个函数在r=a处必须是连续的，对于芯，其“尝试”解为

E=E_cJ_l（qr）exp（±ilφ）expi（βz-ωt）

对于包绕层为

E=E_clJ_l（pr）exp（±ilφ）expi（βz-ωt）

注意到r=a处的边界条件^[5]，再次可以确定p、q和β的容许值。其结果是得到一个有关β与k的关系式，或“色差曲线”，如图8.8所示。数学运算比较麻烦，使用“弱制导近似表达式”稍容易些，主要基于下面的事实：若n₁～n₂，则发生全内反射时，光线在边界的入射角非常大。光线几乎是以掠入射形式向下反射。这表明，该光波几乎是一束横波，在z方向的分量非常小。由于忽略不计纵向分量H_z和E_z，所以数学结果大大得以简化（见图8.7b）。对一级近似，该波是横波，所以，如同三维传播一样，可以很方便地分解成两个线偏振分量。因此，该模式被复制成“线偏振（Linearly Polarized，LP）”模式，表示轮廓强度分布的方法就是线性偏振的表示方法。

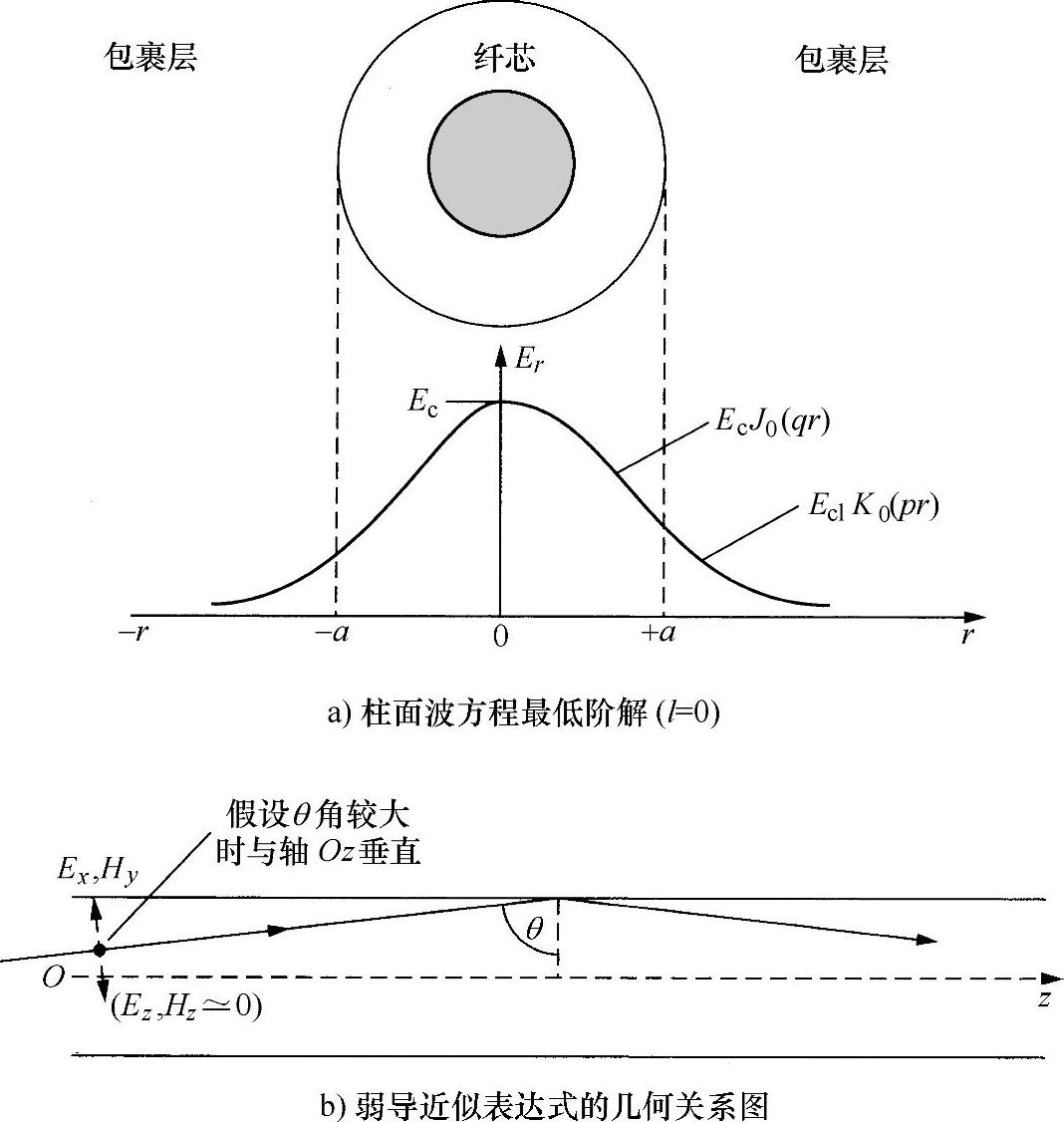
图8.7　柱形波导公式的解和弱波导近似表达式

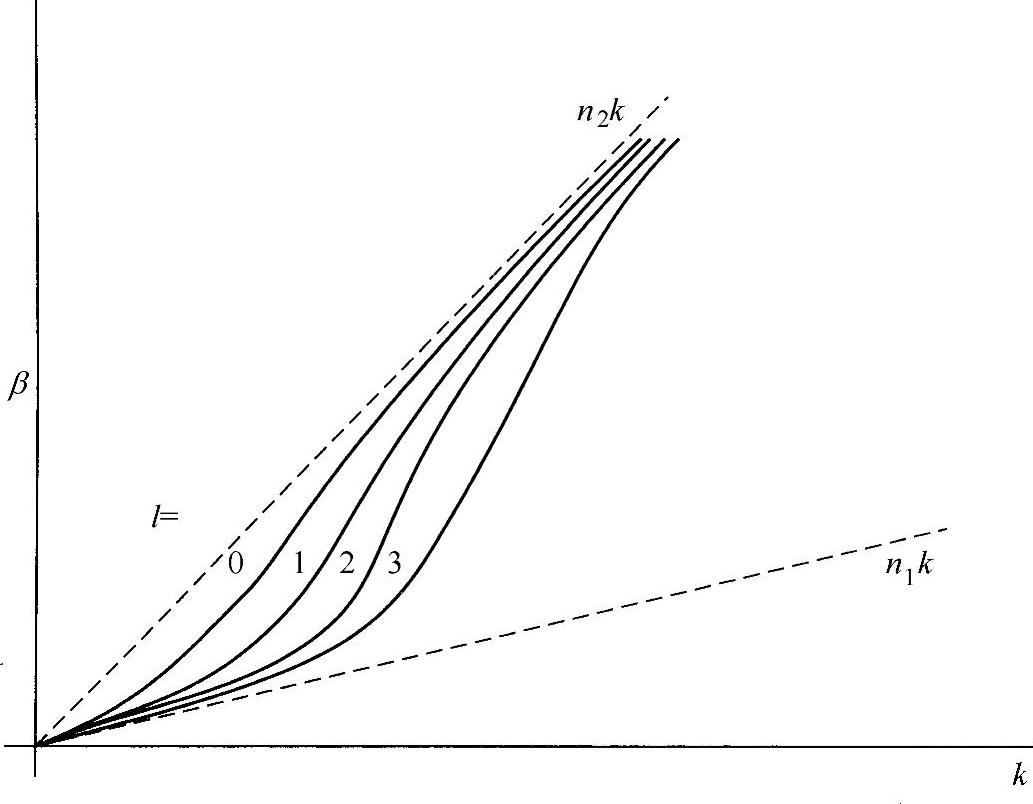
图8.8　柱形波导的色散曲线