平板波导结论与结果，图示和数学求解

为了方便性和完整性，首先，回顾一下本书2.8节对平板波导得出的结论和结果。

再次讨论对称型平板波导，如图8.1所示。此处的波导通道包括一个折射率为n₁的平板材料，外层由两种折射率为n₂的薄层材料所包绕。由式（2.18）可以看出，如果光束在与入射面相垂直的方向是线性偏振（图2.13所示的“横向电场（Transverse Electric，TE）”模式），则由向上和向下传播光线之和得到合成后的电场为

E_T=E_i+E_r

式中

E_i=E₀exp（iωt-ikn₁xcosθ-ikn₁zsinθ）

（即在xz平面传播、与平板界面（平行于yz平面）成θ角的一束波）和E_r=E₀exp（iωt+ikn₁xcosθ-ikn₁zsinθ+iδ_s）这是边界处反射产生的波，并且在两个方面不同于E_i：现在是沿Ox轴的负方向传播，因此x项要改变符号；反射处会造成相位改变，有iδ_s项。还要记住，δ_s取决于角度θ、波的偏振及n₁和n₂，因此有：

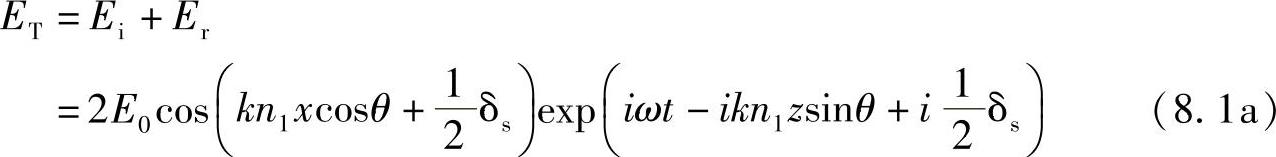
这是一束沿Oz方向传播的波，而振幅按照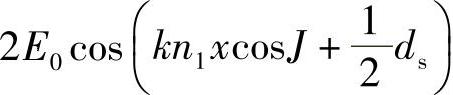规律（见图8.1）沿Ox方向变化。

结构布局的对称性表明，波在两个边界处的强度（电场的平方）一定相同，因此x=0与x=2a处一样，因此有：

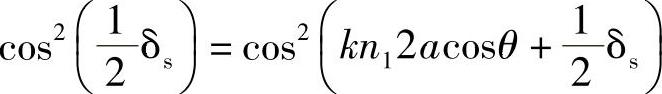
根据本书2.8节得出的结论，这意味着：

2akn₁cosθ+δ_s=mπ （8.1b）

式中，m为整数。这就是“横向谐振条件”，是关于θ的条件（还记得，δ_s也取决于θ），确定一些θ的允许值（对应于不同的整数m），就依次确定了允许的离散传播模式（或者干涉图）。

现在，波在自由空间传播的波数k=2π/λ已经得到修改。首先，介质中光波的波长要比自由空间内的小（频率保持不变，但速度减小一个倍数n_1，2），所以可以很方便地确定：

β₁=n₁k

β₂=n₂k

两者分别代表波导中和外层薄片中的波数。其次，如果认为式（8.1a）能够表述Oz方向上传播的一束波，则在Ox方向的振幅就会得到调制。很方便将波导介质中的波数分解成沿Oz和Ox方向的两个分量，沿Oz方向为

β=n₁ksinθ （8.2a）

沿Ox方向为

q=n₁kcosθ （8.2b）

显然，在这两个分量中，β是沿波导传播的波数，所以更重要些。实际上，现在可以将式（8.1a）写为

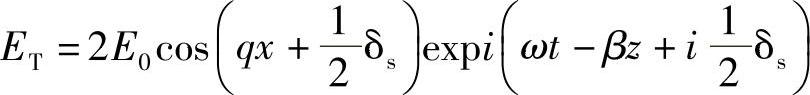
波速是如何沿波导传播呢？显然，由下式给出相速：

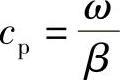
由本书4.3节知道，这并不全面，因为光能量沿波导传播的速度由群速确定，在这种情况下为

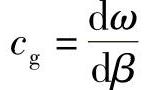
那么对ω和β的依赖关系如何？

为了回答该问题，从式（8.2a）开始讨论：

β=n₁ksinθ

首先注意到，要求所有的实θ都要满足：

β≤n₁k

此外，内全反射条件要求有：

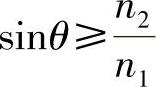
可以得出结论：

β=n₁ksinθ≥n₂k

因此

n₁k≥β≥n₂k

或

β₁≥β≥β₂

该式表明，沿波导轴传播的波数永远位于波导介质β₁与外层介质β₂的波数之间。由于该传播都是部分地在波导介质和外层介质中（损耗波），所以根据物理学也可以得到该结果。稍后，将转向对该问题的讨论。

要记住，此刻关心的是，β如何随ω在这两个限定值之间的变化，那么式（8.2a）还有何用呢？

显然，下面公式可以给出β对ω的依赖关系，但是，对于sinθ呢？

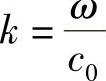
式中，c₀为光在自由空间中的速度。对于给定的m（即一定的模式），横向谐振条件式（8.1b）确定了θ与k的关系。正如所知，由于δ_s是一个以θ为自变量的相当复杂的函数，所以该关系式也非常复杂。因此，为了进一步讨论，必须考虑这种依赖关系。

在本书2.6节已经推导出一定角度下发生全内反射而出现相位变化的表达式，在此重新写在下面，对于电场垂直于入射面的情况：

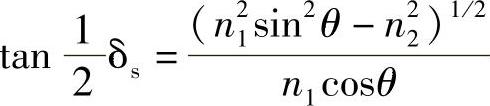
若位于入射面内：

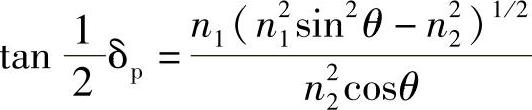
还注意到

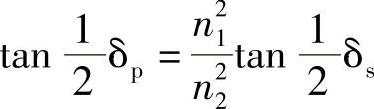
最后，为了方便，定义一个参数p，即(www.xing528.com)

p²=β²-n²₂k²=k²（n²₁sin²θ-n²₂） （8.3）

p的重要物理意义不久会看得非常清楚。

现在，可以将“横向谐振条件”式（8.1b）写成下列形式，若为垂直偏振，则有：

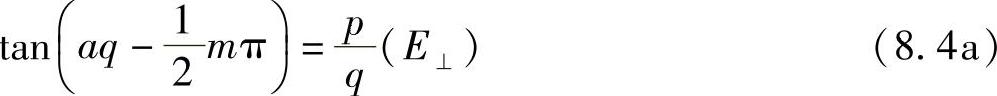
若为平行偏振，则有：

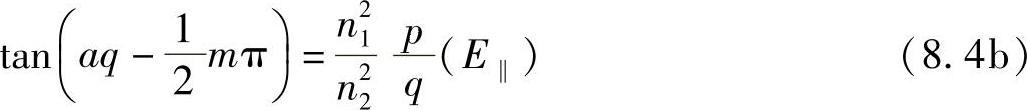
习惯上的波导表示法对上述两种情况规定如下：E⊥定为“横向电场（TE）”，E‖定为“横向磁场（Transverse Magnetic，TM）”。当然，这些项涉及所述场相对于光束入射面的方向。

可以用式（8.4）表示某给定平板结构模式的特性。根据m是偶数或奇数，将该公式的解分成偶数类和奇数类。对奇数m，则有：

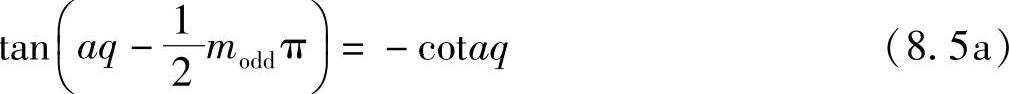
若是偶数m，则有：

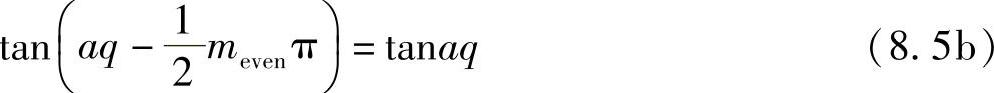
例如，令m为偶数，可以将式（8.4a）写作下面形式：

aqtanaq=ap（E_⊥） （8.6）

根据p和q的定义，显然有：

a²p²+a²q²=a²k²（n²₁-n²₂） （8.7）

取矩形轴ap和aq，则较后面表示p与q之间关系的公式可以转换成半径为ak（n²₁-n²₂）的一个圆（见图8.2）。如果在同一个轴上也画上函数aq tan aq，则在两个函数的所有交点处都满足式（8.6）（见图8.2）（显然，若m是偶数，可以确定一组类似的解）。所以，这些点给出一些θ值，对应着允许的波导模式。对于给定的k值，确定θ值后，就由下式确定β：

β=n₁ksinθ

因此，对于TE模式，可以确定β为k的函数（m一定）。

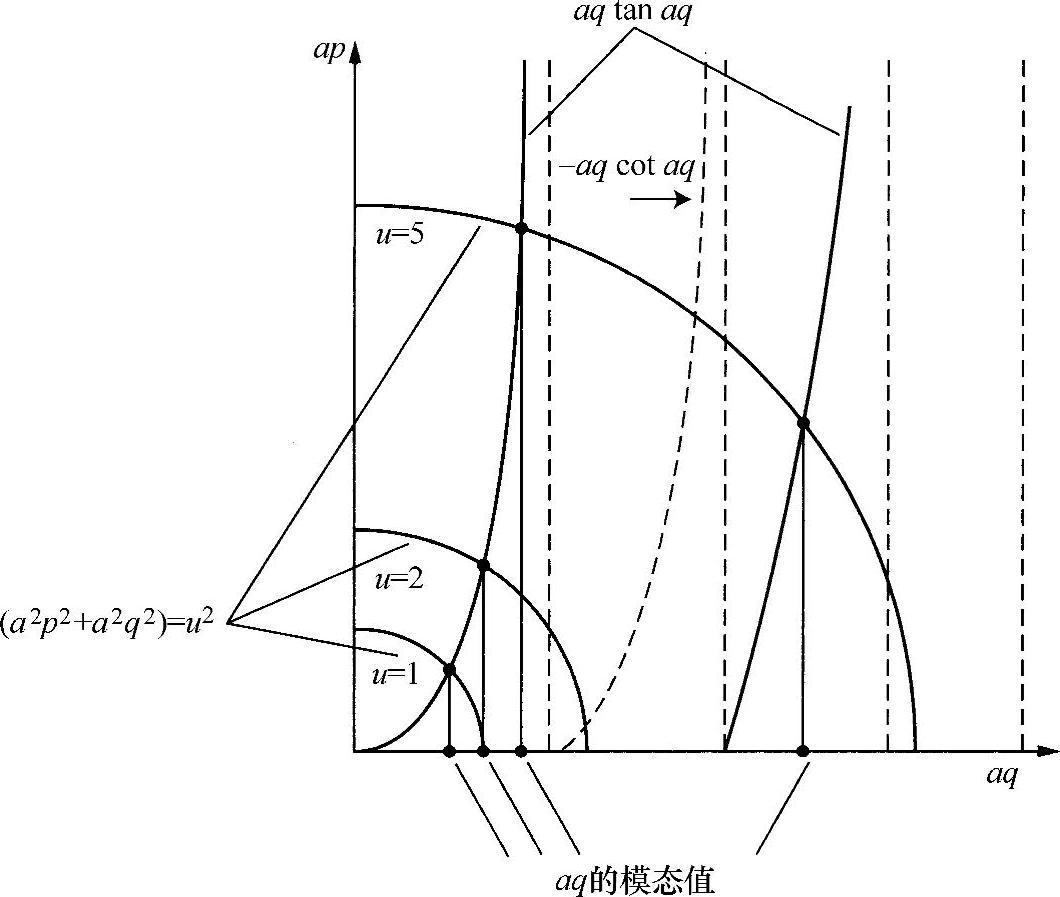
图8.2　平板波导模公式的图形求解

最后，得到：

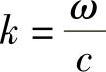
讨论至此，已经得到了β与ω之间的关系。很明显，这就是色散曲线，是波导特性的重要决定因素。或者以β与k，或者以ω与β来做图，利用后一种表示方式对某种有代表性的平板波导绘出的三种最低阶模式，如图8.3a所示。显然，与通过简单微分确定群速dω/dβ相比，这是一种更为方便的形式式（8.3b）。在本章8.6.2节，将单独讨论色差。

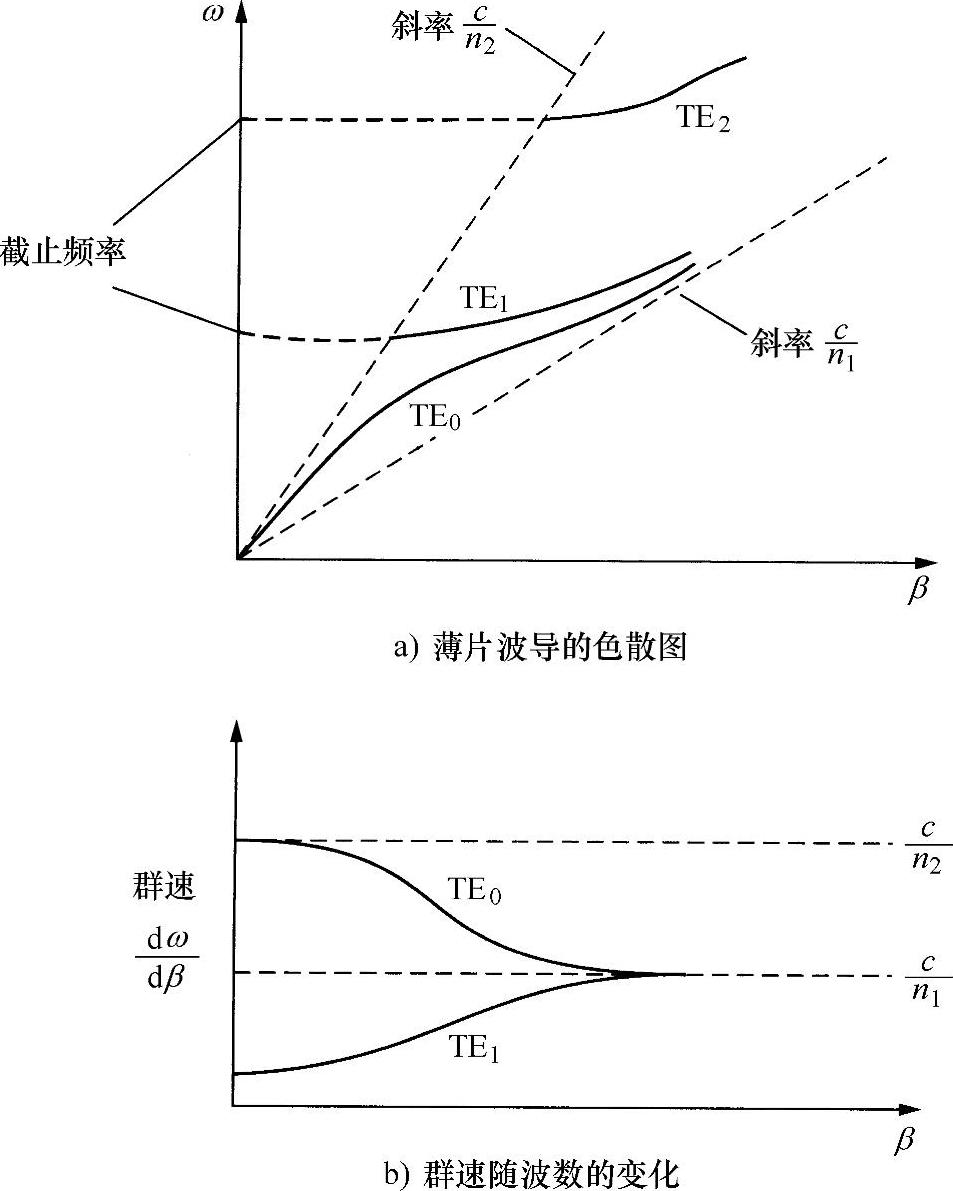
图8.3　平板波导的色散和群速

最后很重要的一点是，随着k增大，下式表示的量也随之增大：

a²p²+a²q²=a²q²（n²₁-n²₂）

随着圆半径（见图8.2）减小，不同的模式连续得到“截止”。当然，k的减少对应着ω的减少，图8.3a所示是很明显的。显然，可能得到的模式数目取决于波导参数a、n₁和n₂。然而，由于该圆总会与正切曲线在一点相交，所以即使一个非常小的圆半径，至少存在一种模式。如果只有一个解，如图8.2所示，圆半径就必须小于π/2，即

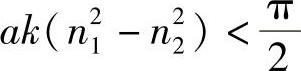
或

这是另一个重要的波导参数。用V表示，称为“归一化频率”，也常简称为“V数”，因此：

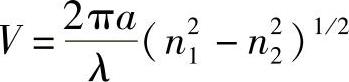
式（8.8）是这种对称平板波导的单模条件。由于波导中恰好只有一种模式，因此代表了一种重要情况，大大简化了其中的辐射特性，如非常方便于信息沿波导的发射。实际上，式（8.8）是阐述（几乎是）未沿波导轴传播的光束不可能产生相长干涉的条件。

显然，利用式（8.4b），可以完成对TE模式的类似分析。

再次分析图8.1所示情况。很明显，在外层介质中也有波传播，距离中心通道越远，介质中的振幅下降得越严重。在本书2.6节已经讨论过这种情况，可以看到，对于连续通过介质边界的场（及其微商），这是必然的直接结果。由式（8.1a）知道，中心通道处的场振幅随下列形式变化：

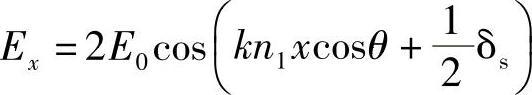
外层薄板材料中的场如何变化？在本书2.6节讨论全内反射现象时已经给出了答案。已经知道，当发生全内反射时，第二种介质中损耗场的振幅根据下面给出的规律下降：

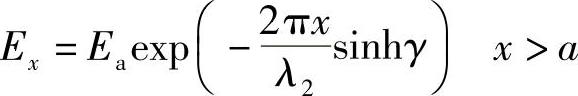
式中

（i）E_a是边界处场的值，即

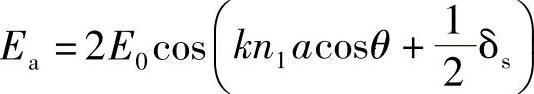
（ii）λ₂是第二种介质中的波长，并且等于λ/n₂。

（iii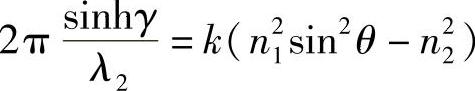），与式（8.3）得到的p是一样的。因此有：

E_x=E_aexp（-px）　x>a

可以看到，p恰好是损耗波振幅的指数衰变常数（见图8.4）。并且，根据式（8.3）可以知道，p≈0.1k（所有在数学上有重要意义的参数总是具有简单的物理意义）。

所以，该损耗波是在外层介质中平行于边界传播的波，振幅随远离边界成指数形式减小。

这些损耗波非常重要。首先，如果总的传播不要受到扰动，为使损耗波在其外层边界处具有可以忽略不计的振幅，则每一个外层平板都要有足够的厚度。该波大约按照exp（-x/λ）规律减小，在x约等于20λ时，完全可以忽略不计（约10^-9）。若是光学波长，该平板的厚度应当≥20μm。其次，由于能量是在外层介质中传播（在Oz方向），所以损耗波的性质将影响核心传播，如关于损耗和色散。在本章8.5和8.6节将详细讨论这些内容。

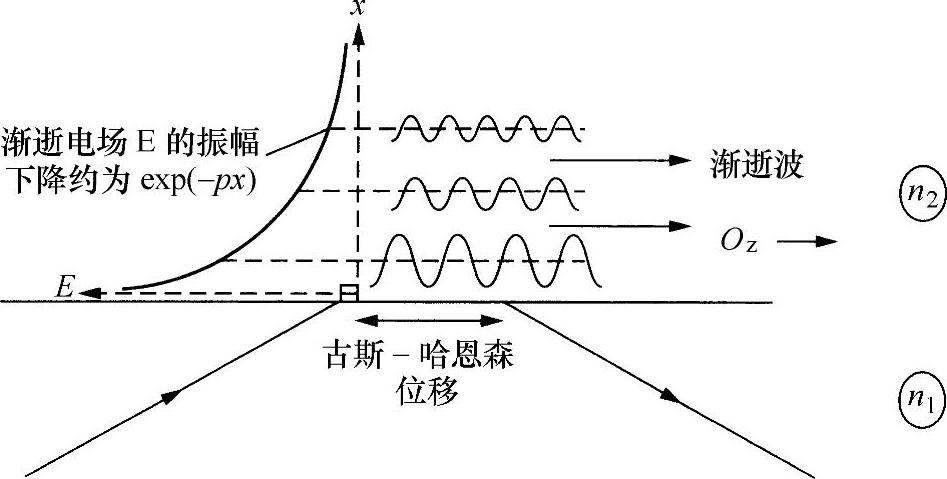
图8.4　损耗波衰变