结型光敏二极管基本原理

重新讨论图7.7研究过的p-n结。当考虑发光课题时要注意，这两类半导体（即p和n）间的接触导致多数载流子通过p-n结扩散，试图使两侧的浓度相等。结果是由于电荷分离而在结两侧形成一个电场。在造成电荷分离过程中一定会导致载流子损耗，所以该电场范围称为损耗区。p-n结随两侧电压趋于平衡，根据本章7.2.2.1节的讨论，该电压由下式给出：

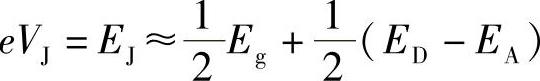
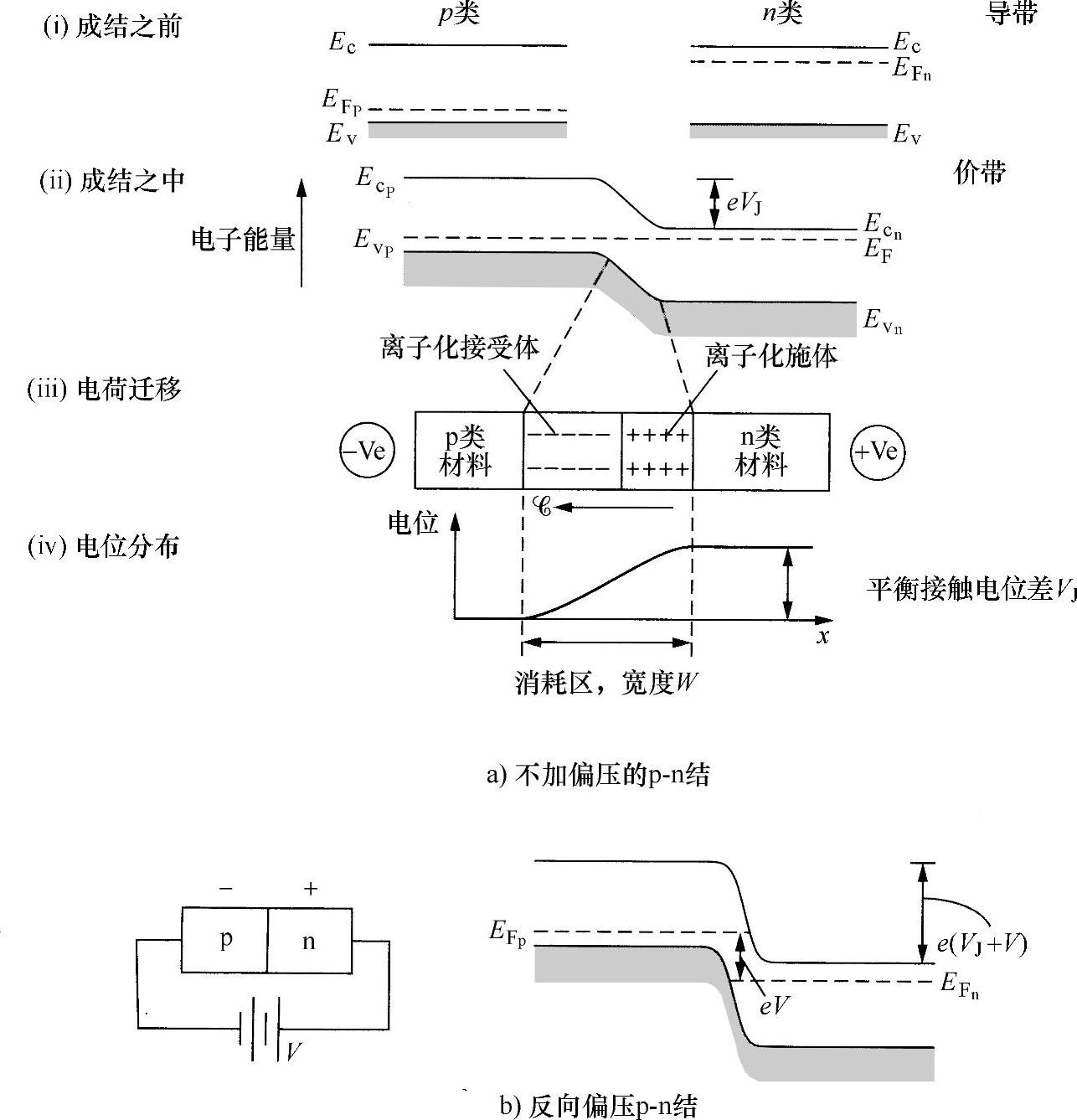
图7.29　应用于光探测的反置偏压p-n结

由前面讨论可知，这种平衡会使p类材料带负电荷，n类材料带正电荷（见图7.29）。假设，一个光子（能量hν）入射到半导体结的电场部分，并满足hν>E_g（半导体带隙）。该光子就形成一个电子-空穴对，并立刻与电场发生作用。结果是电子汇聚在带正电荷的n类材料中，空穴汇聚在带负电荷的p类材料中，从而使结电压下降到低于其平衡值。很容易推导出该电压的降低量。已经知道，处于平衡状态时，结两侧电场产生的漂移电流和其浓度梯度造成的扩散电流是相等的，即i₀。当等效于光功率P的一个光子流入射到结上时，形成的电子-空穴对会受到结两侧电场的作用，因此由式（7.17）确定的漂移电流为

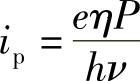
增大为下面的漂移电流：

i₀+i_p

为了适应这种变化，必须增大扩散电流，使系统返回到平衡状态。如果光子流造成的结的电压下降量是ΔV_J，则热能kT会造成更多的载流子穿过p-n结，该电流将增大一个玻耳兹曼因子exp（eΔV_J/kT）（这是费米-狄拉克函数（即式（6.18b））在分布尾部，即各自能带上的良好近似）。因此，扩散电流增大为

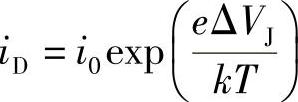
所以，新的平衡要求为

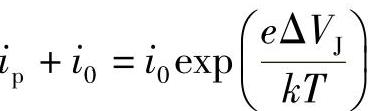
或(www.xing528.com)

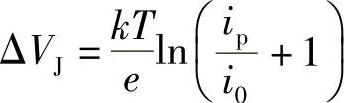
式中，i₀为某种材料的常数，测量ΔV_J就得到i_p，因而得到P。然而，ΔV_J与P之间的对数关系是非线性的，因此“光压”操作模式对测量P是不方便的。当然，该模式的确有比较简单的优点（无需提供电源），并用于某些特定的应用领域。

下面阐述一种更为方便的结构布局是“光导”模式。

再次讨论p-n结，并施加一个反向偏压（约10V），（即施加一个使p侧相对于n侧是负值的电压），所以阻挡载流子穿过p-n结（见图7.29b）。由于施加的电压会将两种符号的载流子拖离p-n结，所以这种作用使两种相反结电流降到非常低（“泄漏”），并增大损耗层的宽度。如果具有足够能量的光子入射到损耗区，则形成的电子-空穴对立刻被分成各自的组分电荷，快速接近p-n结具有相反电荷的一侧。这样，反向偏压会打破平衡。在没有光子产生载流子时，只有非常小的扩散和漂移电流。原因是两类材料之间的载流子已经增多，损耗层已变宽，惟一流过的电流是由于输入光子形成的电荷，所以该电流正比于输入的光功率。对于大部分测量，这是一个非常方便有用的关系。

这种布局的另一个优点是，这些电荷快速分离，几乎立刻被p-n结端部大量带有反向电荷的载流子湮没，从而减轻了再组合过程中的随机性。并且，与光电伏打（photovoltaic）情况相比，导致更小的“再组合噪声”。

光导光敏二极管的响应速度取决于几个因素。一个限制因素是损耗层两侧发生变化的漂移时间（见图7.30），因此，在灵敏度和响应时间之间再次遇到矛盾。随着反向偏压增大，电荷的漂移速度随之增加，直至饱和（对于硅，速度约为5×10⁴m/s）。

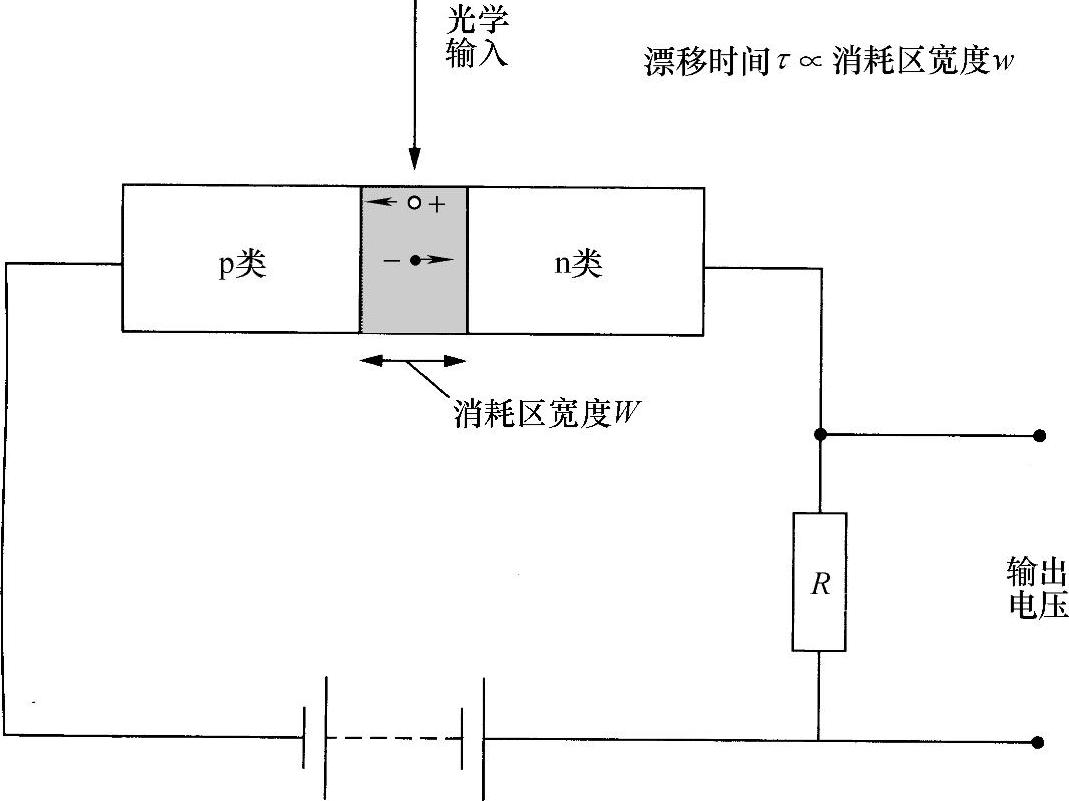
图7.30　光敏二极管响应时间与损耗层宽度的关系

至此，增大偏压只会增加损耗层的宽度而不会增大漂移速度，所以响应时间会增长（带宽会减小）。另外，损耗层宽度越大，适合接受入射光的空间（体积）就越大，可以形成的电子对数目也就越大，灵敏度也随之越高。此外，在损耗层之外也会形成一些电子对。若在该区域扩散范围内形成（在再组合之前能够通过扩散传播到该距离），则载流子将进入损耗层区域，并对形成电流有所贡献。这种贡献可以视为光敏二极管（对锐脉冲）响应上一个相当特殊的“尾部”，通过增大反向偏压可使其减小，从而增大了损耗区相对于扩散区的宽度（另一种方法是利用“PIN”结构，下面将会介绍）。

典型的硅光电二极管结构如图7.31所示。在重掺杂（p+）p类材料和低掺杂n类材料之间形成p-n结，所以损耗层就扩展到n类区域。显然，p⁺区非常薄，以便于使光穿透到损耗层内。底部的n⁺区确保金属电极与n+间有良好的电接触。

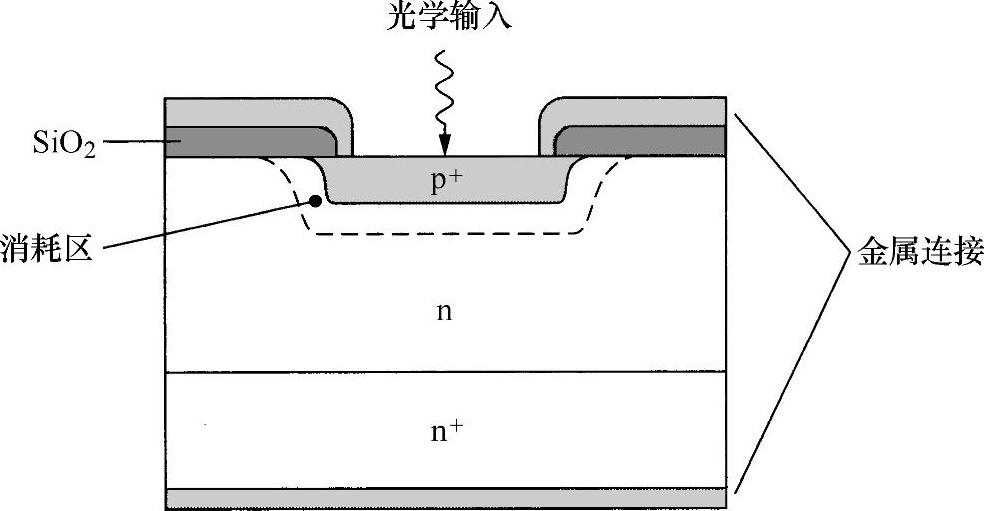
图7.31　硅光敏二极管的结构