光子学设计基础:拉曼-奈斯结构解析

讨论图7.18所示的结构。光波入射到正在传播正弦声波的某介质上，光波的传播方向与声波方向垂直。现在，如果介质厚度小于几百个声波波长（本书称为“薄”介质），则对于光波，该介质层就称为薄衍射孔径。当然，声波会以正弦相位函数形式造成孔径的衍射功能。很难精确分析以正弦相位变化形式组成的衍射光栅：由于必须以正弦（或余弦）函数的正弦（或余弦）函数形式表示，所以包含了贝塞尔函数，这将在后面稍作介绍。然而，利用物理学方法可以相当容易地推导出初级性质，图7.19所示就是这种情况。显然，如果沿孔径选取一组点，彼此间距是λ_A（声波波长），则各点的光波具有相同的相位。

从这些点出发，并与光栅法线成θ角度出射的光线能够产生相干的条件为

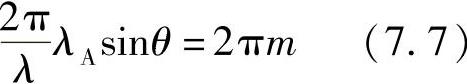
式中，λ为光学波长；m为正或负整数。

对于其他任何一组点，沿孔径方向逐点的折射波相位都是变化的。因此，在孔径范围内取平均值，将相互干扰，得到接近零的振幅。由式（7.7）得到具有衍射极大值的方向θ_m为

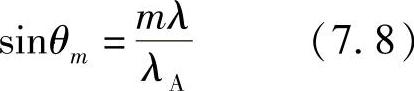
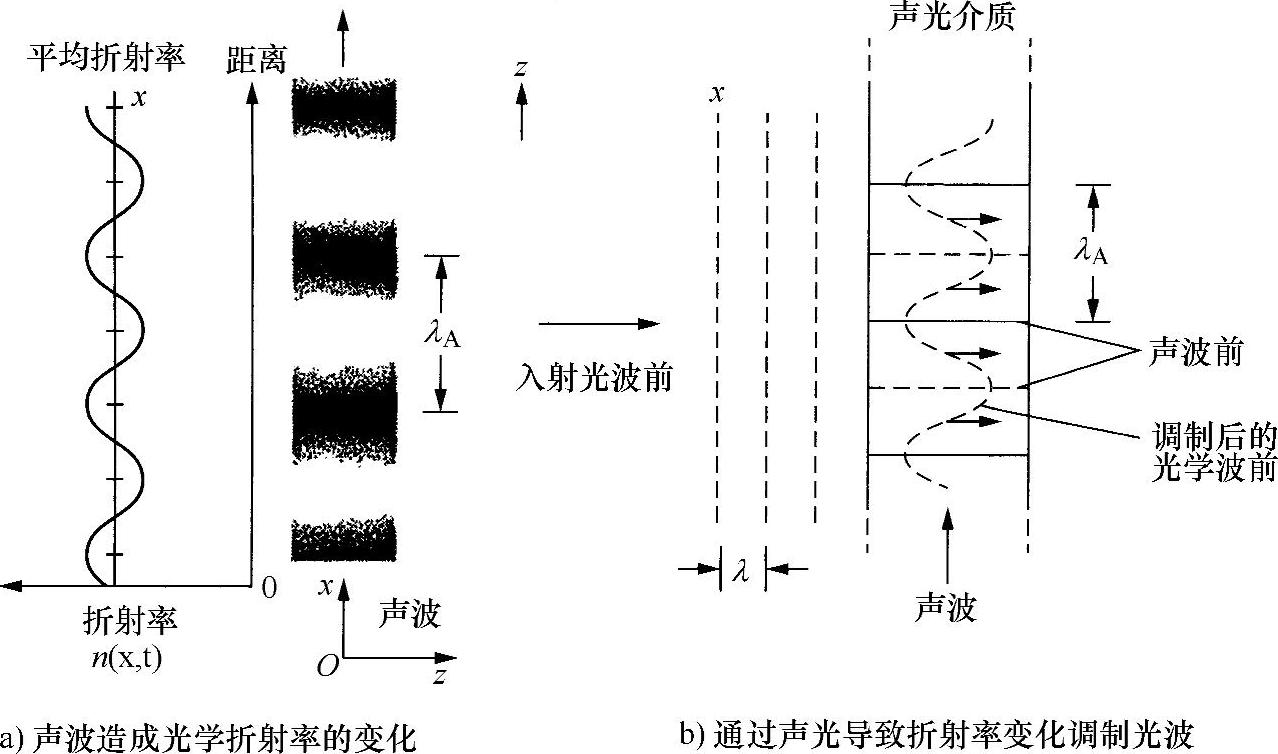
图7.18　声光调制的基本原理

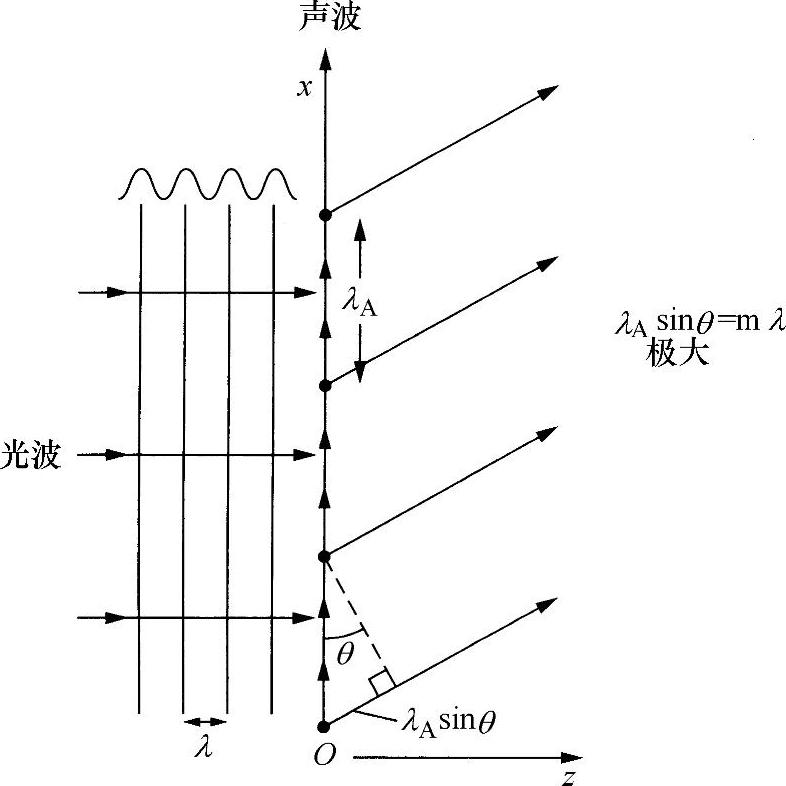
图7.19　拉曼-奈斯声散射中相长干涉的条件

显然，包含了m=0的情况（即某些光没有发生反射，形成了“直接透过”部分）。

当然，这种结论有助于确定究竟有多少光偏转到不同的衍射级中，只要进行正确的分析，很快可以得到这些信息。在此开始之前，关于衍射过程，还有一个重要事情需要注意。

声波通过介质进行传播，实际上声光栅是在移动的。当一个移动表面使一束波发生偏折时，会产生多普勒（Doppler）频率漂移，并由下式给出漂移量：

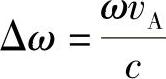
式中，v_A为该组点在声波传播方向上的移动速度（因此等于声速）；c为光在介质中的速度。对于以θ_m角衍射的光，声速在光传播方向上的分量是v_Asinθ_m（见图7.20）。

由于v_m较小，利用式（7.8）有：

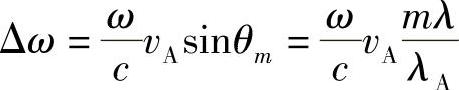
即

Δω=mΩ

式中，Ω为声角频率。频移是衍射级乘以声频。还注意到，对于负偏转（即θ_m和m都是负的），频率减小；而对正偏转（“增大（或正值）”），频率是增大的。因此，除了偏转调制外，还有频率调制。偏转角越大，频率漂移越大。

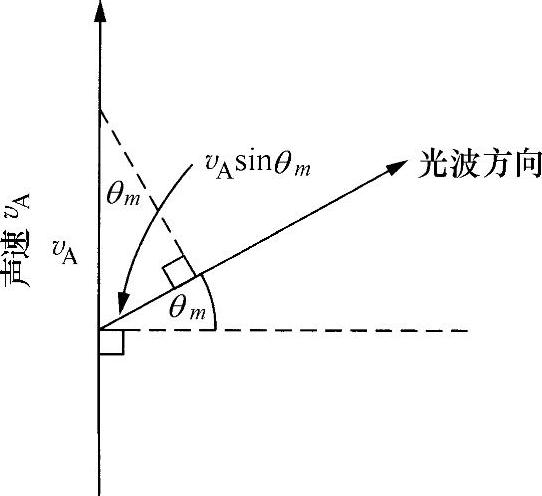
图7.20　多普勒漂移的速度分解

通过数学方法可以正确地对所有这些量完成定量计算：

假设，声波在Ox方向通过介质进行传播（见图7.18），因此扰动后的折射率如下：

n（x，t）=n₀+Δnsin（Ωt-Kx） （7.9）

式中，n₀为未受扰动介质的折射率；Δn为与角频率为Ω、波数为K的声波振幅成比例的折射率扰动。

一束波长为l的光波在与声波相垂直的方向通过介质传播，根据下面形式形成相位扰动：

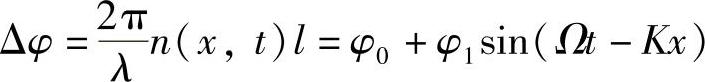
式中，l为介质中的光路长度。并且，由式（7.9）有：(www.xing528.com)

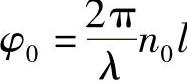
和

φ₁正比于声波振幅。

假设，沿Oz方向入射在介质上的光波写成下面的指数形式：

E=E₀exp[i（ωt-kz）]

一旦从介质中沿Ox方向以扰动后的相位出射，就会变为

E=E₀exp{i[ωt-kz-φ₀-φ₁sin（Ωt-Kx）]}=E₀exp[i（ωt-kz-φ₀）]exp[-iφ₁sin（Ωt-Kx）]

第二个因子给出sine（或者cosine）的sine（或cosine），因此含有贝塞尔函数。实际上，利用众所周知的数学恒等式可以将E表示成下面的因子形式（见参考文献[1]）：

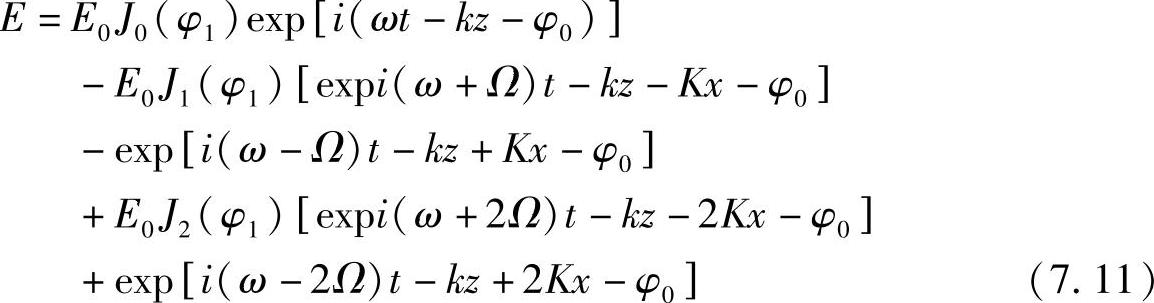
其中，J_m（φ₁）是相位扰动幅角为φ₁的贝塞尔函数，并且是图7.21所示的形式。这就是确定究竟有多少光偏转到第m级的J_m（φ₁）因子。显然，根据J_m（φ₁）的形式，光振幅不会总是随着φ₁的增大而增大。倘若声波的功率不是过分高，由于“薄”介质会导致式（7.10）中的光路长度l有较小的值，所以拉曼-奈斯结构形式的φ₁通常都会较小。偏转后的光振幅也比较小，其余的大部分光未发生偏转。事实上，如果φ₁<<π/2，则有：

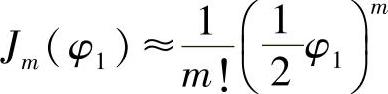
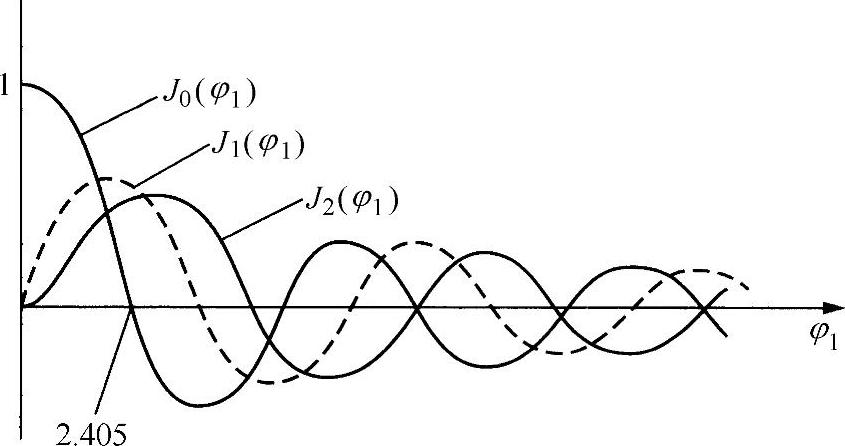
图7.21　（一类）贝塞尔函数：前三级

因此

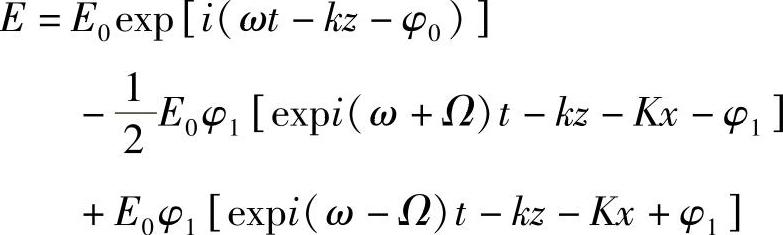
所以，偏折到初级模式中任何一级的功率与未发生偏折级功率之比为

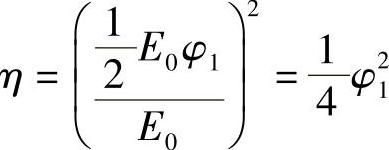
由式（7.10）得

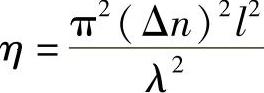
因此，对于初级近似，在这些第一偏折模式中的功率正比于由声波造成扰动后的振幅平方，所以也正比于声波的功率。

偏折角也比较小。现在计算一个实际例子。假设，λ=633nm和λ_A=0.5nm（对应的硅中的声频约10MHz），由式（7.8），得到θ₁=±1.7mrad=0.07°。

最后，讨论式（7.11）。注意到，每一级m的光学频率为

ω±mΩ

从而确认了早期由物理理论得到包括多普勒效应在内的结论。

参考式（7.11）及图7.21所示的贝塞尔函数，注意到，对于某一给定的φ值，J₀（φ₁）=0，若满足该条件将没有光发生折射。出现该现象的第一个φ₁值是2.405，并且需要很大的声功率。

在拉曼-奈斯结构中，声光效应可以使设计者通过控制声波的振幅和频率同时调制光波的偏转、振幅和频率，这是一种非常有意义的通用光学调制形式，得到了广泛应用。

然而，对于这类衍射，衍射材料的厚度要相当小，因此声光的相互作用长度相应也小，调制作用较弱。当声频较高并具有较小的声波波长时，与系数λ²_A/2πλ（见参考文献[2]）相比，其厚度一定非常小，所以该结论尤其正确。前面曾经给出过一个例子，在声波频率为10MHz时λ_A=0.5mm，光学波长为633nm，可以确定厚度t<<63mm，所以约5mm的值是较实际并可以接受的。然而，在50MHz时，t<<2.5mm，即较合适的值是0.2mm，这是一个非常脆的硅片，很容易被声波击碎。因此，对于较强调制，特别是较高频率时，习惯上就变成较厚材料的情况。