电光调制器-光子学设计基础

在本书3.10.1节中已经简要介绍过电光效应。为了理解其在电光调制器中的专用性，必须更详细地讨论这种现象。

如果对某种介质施加一个电场，其作用是产生线性双折射，所以将会产生两个线性正交的光学偏振态，不会改变传播形式而是以不同速度传播。如果该介质是各向同性（非晶体或对称晶体）的，则这两种本征态分别平行和垂直于电场方向；若是晶体材料，本征态偏振方向将取决于晶体结构特有的对称性。

当然，可以用折射率差Δn表示同一材料中的两种不同速度。利用每种情况中Δn对电场的依赖性区别两种最重要的电光效应：一种情况中，依赖关系是线性；另一种是二次方关系。相应公式如下：

Δn=PE　泡克耳斯（Pockels）效应 （7.2a）

Δn=KE²　克尔（kerr）效应　（7.2b）

式中，E为施加的电场；P和K分别为泡克耳斯系数和克尔系数。在学术论文中，常用λB代替K。其中，λ是光波波长，此情况下B称为克尔系数。其原因是，在距离l内的相位变化可以写成（2π/λ）λBE²l。因此，对于一级近似，就与λ无关。然而，在某种程度上，B仍然与λ有关，取决于使用波长下的介质色散。

利用修改Δn如何设计一个调制器？

很明显，相位调制非常容易，如图7.14所示。线性偏振光入射到施加有横向电场的一种材料中，偏振方向平行于施加电场产生的双折射本征轴中的一个。该场产生的光学相位变化为

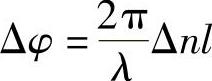
式中，l为材料中的光路长度；λ为光波波长。

由式（7.2a）可以看到，泡克耳斯效应将有：

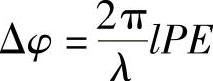
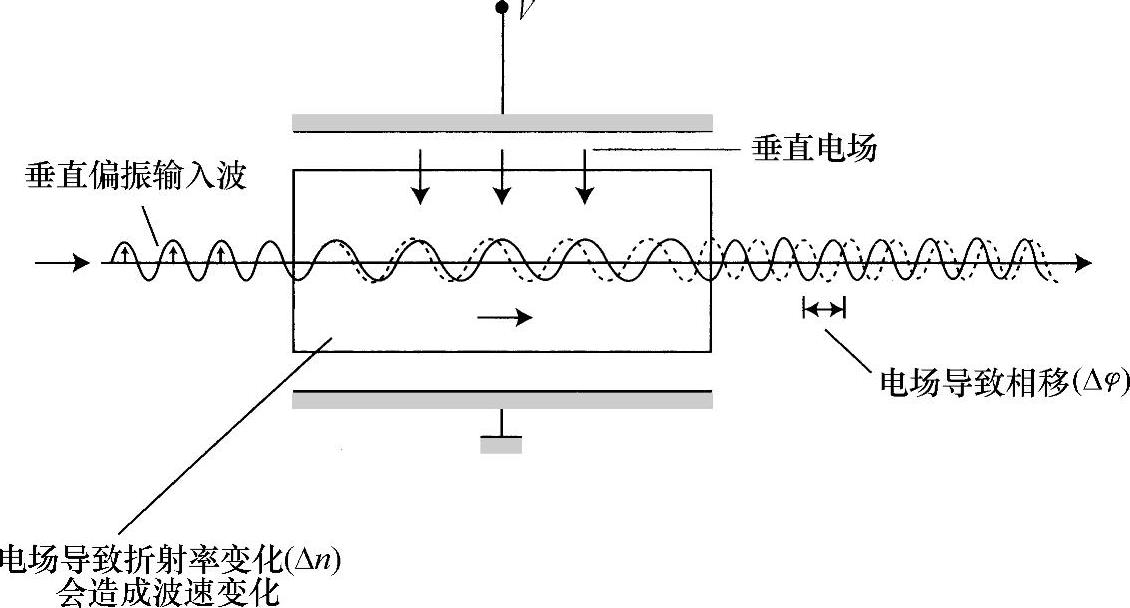
图7.14　利用电光效应进行相位调制

若E是施加在宽度为d的材料上的电压V，则有：

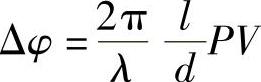
相位变化正比于施加的电压。当然，如果希望传递的信息呈电压波形形式，则问题会变得相当一般。

然而，也有可能利用电光效应调制波的振幅，如图7.15a所示。线性偏振光以与施加电场产生的本征轴成45°角入射，其结果是，在与双折射本征轴方向对应的两个偏振元件之间插入了一个相位差，线性偏振波变为椭圆（一般）波偏振，所以该光得到了偏振调制。

假设，放置一个偏振分析仪，使出射光在入射到光探测器之前通过该仪器。还要假设，该分析仪的接受方向与初始的入射偏振方向为90°角。所以，未施加电压时，没有光通过分析仪投射到探测器上。一旦施加电场，偏振就变成椭圆偏振。由于在接受方向有一个分量，所以一定有一些光会通过分析仪（一个真正的椭球在任何方向都有非零振幅）。下面，对这种重要情况给出正确的定量分析。为了简单化，假设使用的电光晶体材料本身没有双折射。电场在Ox和Oy方向感应产生双折射，而光在Oz方向传播。输入的线偏振光的偏振方向与这些轴成45°，所以每个本征轴方向的分量可以写为

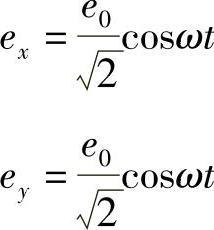
式中，e₀cosωt代表输入波。一旦从施加有电场E的晶体中有光出射，就可以将波写为

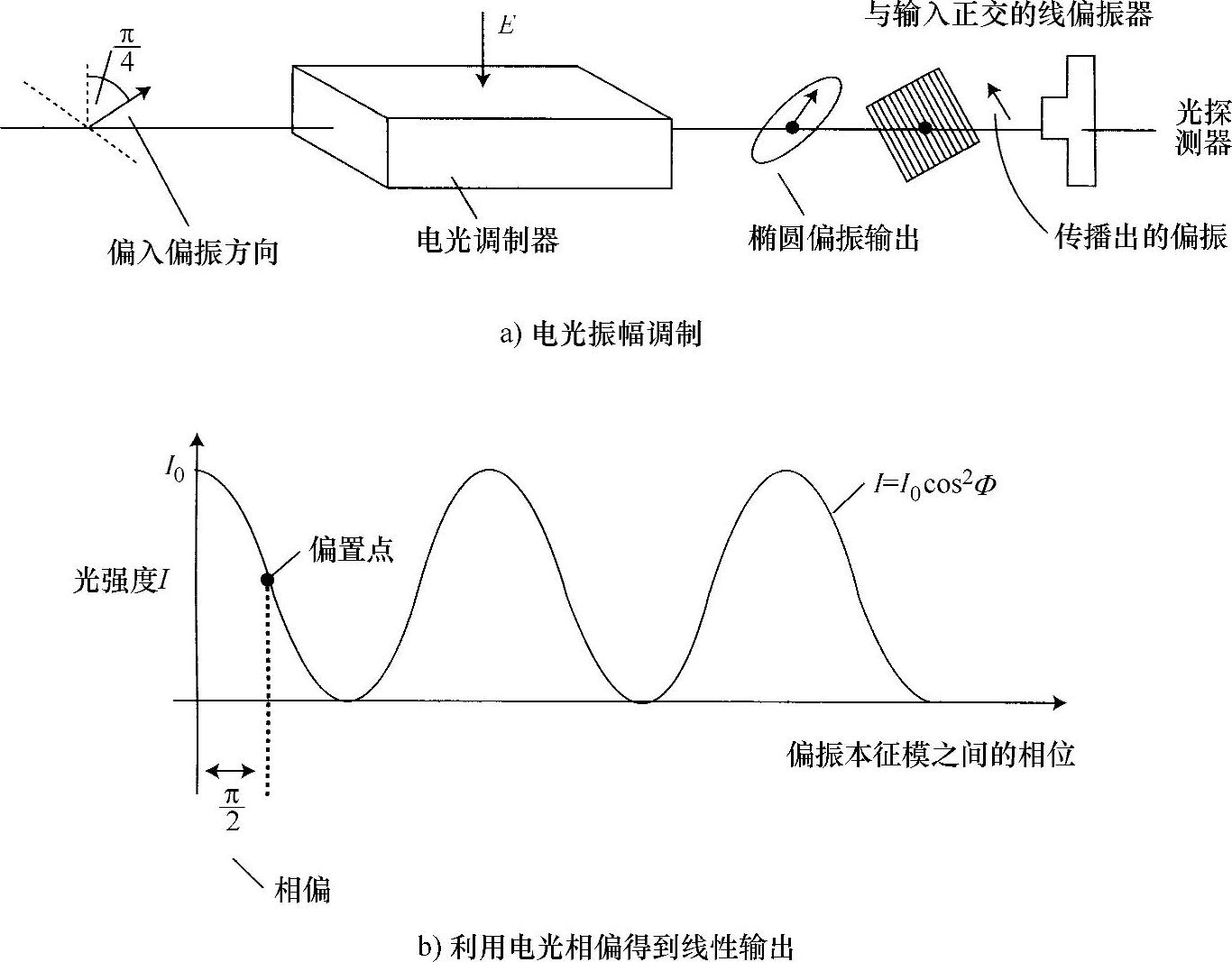
图7.15　线性电光振幅调制

式中，δ表示未施加电压时晶体引入的相位延迟（因而两个轴是一样的），并且φ为

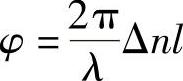
其中

Δn=KE²

或

Δn=PE

这取决于过程中是泡克耳斯效应还是克尔效应。

根据式（7.3），与初始入射的偏振方向成90°放置的偏振分析仪将会允许下面的光通过（见图7.15a）：

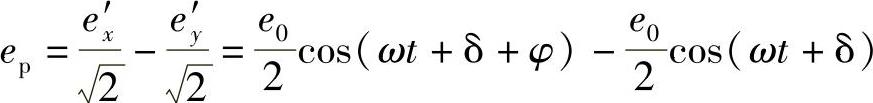(www.xing528.com)

利用初级三角公式：

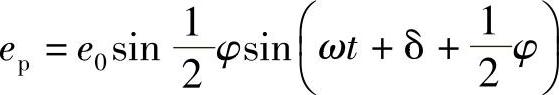
因此，入射到探测器上的光强度为

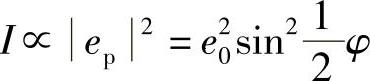
现在，φ正比于E（泡克耳斯效应）或者E²（克尔效应），对于I与E之间的关系，这并非一个满意的结果。因为该项使其有严重的非线性，并且I并不能完全代表施加到调制器上的电压信号，需要的是I与E之间具有直接的比例关系。可以这样设计两者之间的关系：假设，在光到达分析仪之前已经在偏振组件之间插入一个延迟π/2的偏压相位。这样，未施加电场时，光以圆偏振形式到达分析仪，施加一个电场后有：

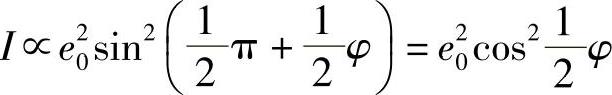
因此

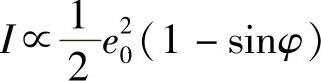
如果φ比较小，则

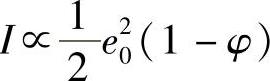
现在，光探测器接收到一个稳定的、正比于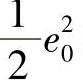的光强度。I随φ变化，因此也随E和E²变化，有：

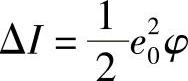
选择一个位于cos²变化范围内并且一级近似是线性的偏压点（见图7.15b）。

若是泡克耳斯效应，如前所述，则ΔI正比于E，即正比于电压。显然，探测器接收的光学功率的变化恰好是ΔI乘以探测器的有效面积。

若是克尔效应，则变化正比于电场（因此也是电压）的二次方。然而，可以利用同类偏置电压法进行校正（必要的话）。此时，偏压施加在外部电场上。如果施加一个稳定的电场E₀，则有：

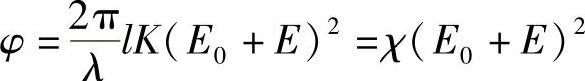
式中，E为信号（调制）场。可以得

φ=χ（E²₀+2E₀E+E²）

若E₀>>E，则有：

φ≈χE²₀+2χE₀E

因此，φ的任何变化都与E成正比，这正是所需要的。应当记住，对于特定应用，这种设置偏压的技术对调整不方便的二次方率关系是一种非常有用的方法。

通过使泡克耳斯效应材料的相位延迟，以及克尔效应材料的相位延迟和电场偏置，有希望设计出一种电光调制器，使其光强度正比于施加的电压。若是这样，应当选择何种材料呢？

大体上说，最为方便的是使用具有高线性（泡克耳斯）电光效应的材料，典型例子是磷酸二氢铵（Ammonium Dihydrogen Phosphate，ADP）、磷酸二氢钾（Potassium Dihydrogen Phosphate，即KDP）、铌酸锂（LiNbO₃）、钽酸锂（LiTaO₃）、硫化锌（ZnS）和砷化镓（GaAs）。施加几个（1～10）电压就可以获得满意的响应。然而，正如本书3.10.1节指出的，只有非中心对称的晶体才表现出泡克耳斯效应，而所有材料都呈现克尔效应。所以，实际应用中常常更容易接受后者。此外，无定形材料，诸如熔凝石英的克尔效应通常都非常快，对外场响应仅有几个毫微微秒（约10^-15s）。由此得出结论：借助克尔效应可以设计出非常快的开关。当然，对于开关，没有必要使光强度随施加电压线性变化。要求很简单，就是让该场造成相位延迟π，所以线性偏振方向旋转π/2，而无法通过分析仪（见图7.16），从而给出“on（开）”和“off（关）”的状态。某种调制器完成该功能所需电压称为半波电压V_λ/2。

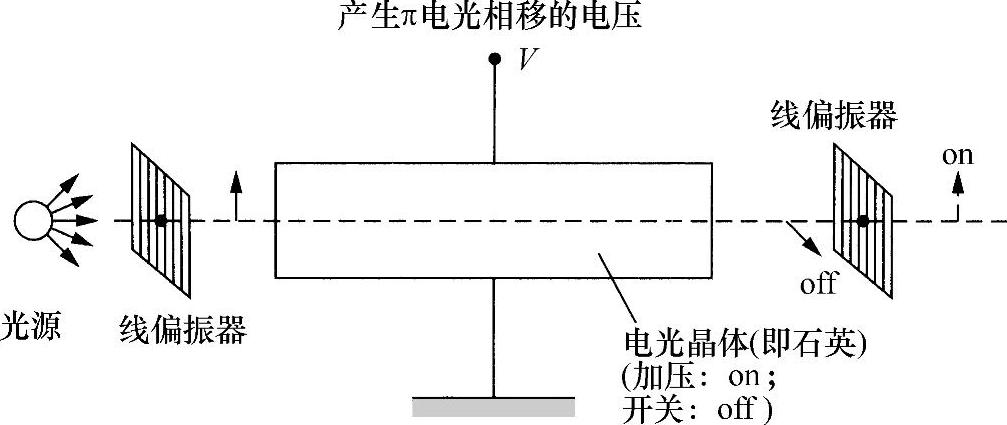
图7.16　双态电光开关示意图

最后，讨论电光系数P和K的单位。式（7.2）对这些量进行了定义，由于Δn没有量纲，显然，P的量纲是m/V，K的量纲是m²/V²。铌酸锂的泡克耳斯系数是3.26×10^-11m/V，硅玻璃的克尔系数是2×10^-22～9×10^-22m²/V²。

作为例子，假设是一个非常快的双态光学开关，光波波长是633nm。在硅材料中使用克尔效应，立方体硅材料的边长为10mm。需要的电压为多少？

据此有：

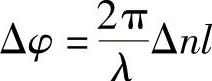
和

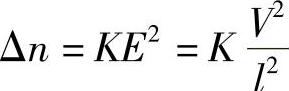
式中，V为电压；l为立方体的边长。若Δφ=π和K=5×10^-22m²/V²，则V=2.52MV！速度并非完全没有问题。