光子学设计基础：p-n结介绍

若有一块由相同本征材料制成的p类和n类半导体，换句话说，一块硅掺有三价原子（如硼或锗），另一块掺有五价原子（如磷或砷）。假设这两块半导体的平面端彼此密切接触，形成一个p-n结件。当然，还会记得，两种材料的费米级不同：在p类材料中，费米级位于价电子带与受主级之间的中间位置；在n类半导体材料中，则位于施主级和传导带底端之间的中间位置。下式给出两种材料的费米级之差：

式中，E_C为传导带低端的能量；E_D为施主级；E_A为受主级；E_v为价电子带顶端处能量。因此有：

式中，E_g为材料“能隙”（E_C-E_v）；因此，E_J约为能隙的一半（见图7.7a）。然而，在本书6.3.5节曾讨论过，对于本征材料，随着温度升高及受主级/施主级消耗殆尽，p类和n类两种材料的费米级容易返回到该值（任何一类材料的费米级都会变成相同的该值），因此E_J→0。显然，在n类材料中，电子是多数载流子，而在p类材料中是少数载流子；若是穴，情况正好相反。很清楚，两类载流子通过p-n结时必须达到平衡。

图7.7　p-n结和发光二极管

正如本书6.3.2节所述，费米级位于费米-狄拉克“尾部”的中心（即电子态占有率为0.5的位置）。（在T=0处，代表最高的占有能量级。）当两类半导体密切接触时，n类材料传导带中的一些电子，会得到p类材料价电子带中的某些新态（穴），因而这些电子就落入穴中。显然，为了完成该过程，它们必须散射到p类材料中。对穴而言，对应的散射也是成立的。所以，在彼此接触的范围内，穴和电子重新组合，导致电荷载流子缺乏。其结果是，在称为“损耗区”的p-n结区域附近，电阻变得很高。

在损耗区，确立了一种新的电子平衡分布。显然，在两种费米级相等后（见图7.7b），一种给定的电子平衡状态只有一种费米级，所以该系统只能处于平衡状态。然而，在这些条件下，为了使p类材料中的正性穴中性化，负性电子将会离开n类材料。由于这些材料在电性能上一定呈中性，因此就要使每种材料都带电，n类材料带正电，p类带负电。如此，通过损耗区一定存在电压，并等于费米级间的初始差别E_J，约为半个带隙数量级（0.1～0.3V，取决于材料），称为“接触”电势。可以看到，其结果是动态平衡，电子从n类材料散射到p类材料，但是，这种“扩散电流”因扩散而使电压反向。电压在损耗区两侧形成一个电场，作用在电子和穴上，导致一个逆向“漂移电流”。上述两种电流在平衡时是相等的，并且，正如已经注意到的，由于损耗区的电阻很高，所以，电流相当小。

也可以根据p-n结两侧的电子浓度或者穴的浓度表示接触电动势。首先，讨论n类材料中（多数载流子）电子浓度为n_n和p类材料中（少数载流子）电子浓度为n_p的情况。由于费米级非常靠近带隙中心，传导带底端和价电子带顶端到费米级的距离相当远，应用费米-狄拉克分布尾的布里渊近似表达式（式（6.18b）），可以得出结论，在温度为T的热平衡状态下，用下面形式将n_n与n_p联系在一起：

式中，V_C为接触电势。因此有：

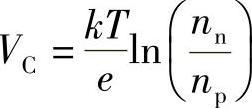
当然，同样的讨论可以应用于穴浓度p_p和p_n，所以有：(www.xing528.com)

（注意，两个公式中的p-n反转）

一定会得出结论：

p_pn_p=p_nn_n

由式（6.27b）可知，该公式是正确的。

很容易用掺杂浓度表示接触电势。假设，施主（n类）和受主（p类）浓度分别是N_d和N_a。对于n_n=N_d的大多数情况（即n类非本征半导体材料中的所有电子都由施主原子提供），可以有一个非常好的近似。根据式（6.27b），有：

pn=n²_i

所以，在p类材料中有：

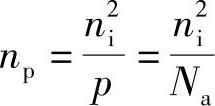
在这种情况下，所有穴都由受主原子产生。将这些n_n和n_p值代入上面给出的V_C表达式中，得到：

此即损耗区的两侧电压。

损耗区有多宽？显然，这取决于电子散射的难易程度、费米级的位置及载流子浓度，但宽度的典型值是几个微米。此外，与每侧大块材料相比，由于损耗区的电阻很高，几乎所有的结电压都产生在结上，其余材料没受到影响。费米级相当快地（但平稳地）反转到结两侧各自的初始能级。