半导体电子能级分布-光子学设计基础

根据布里渊区图，能够对半导体中的电子能量分布和费米级位置得出何种结论？该课题的完整数学处理相当复杂，并且多少会忽略其重要的物理意义，所以在此给出的表述集中在物理意义方面。

显然，根据布里渊区图可以知道，计算自由电子所依据的简单关系式E/k不再成立，所以，与自由电子的情况相比（见式（6.16b）），态函数密度的计算将变得更为复杂。事实上，任何一个容许能带的作用都相当于一个有效约束电子的“箱体”，态密度函数从能带边缘开始，以零能量为始点，以类似式（6.16a）自由电子函数的方式成抛物线形式增大。其结果是，在价电子带顶端边缘附近和传导带底部边缘附近的态密度函数会是图6.18所示形式。为了确定这些能态中的电子能量分布，态密度函数Z（E）必须乘以式（6.19a）所示的费米-狄拉克占有率函数。因此，电子能量分布由下式给出：

n（E）dE=Z（E）F（E）dE

如果单位体积内的电子总数N_T为

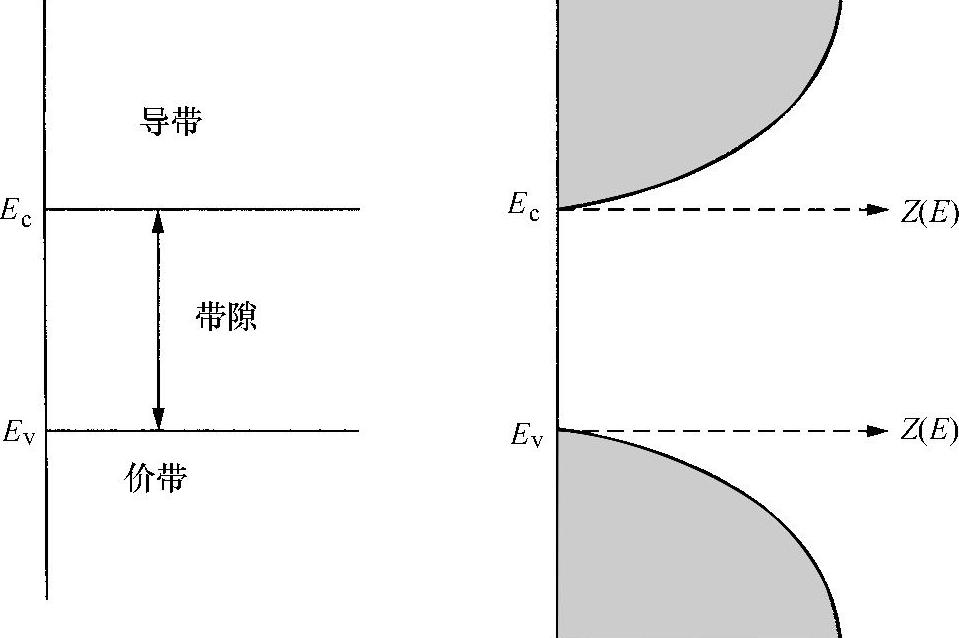
图6.18　一种带结构的态密度函数（Z（E））

并且

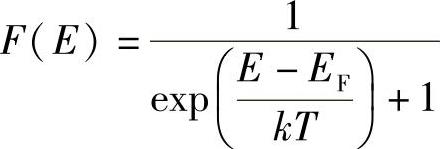
所以，式（6.23）就是根据N_T表述E_F的表达式。N_T随单位体积内原子/分子数及每个原子/分子中的电子数变化，因此不同材料是不一样的。可以计算各种材料的E_F，但是，要记住本章6.3.2节强调的注意事项：固体是一种复杂材料，晶格间隔随方向变化，因此布里渊区也随方向变化，随之Z（E）及E_F都会随方向而改变。一般地，必须看作是复杂的三维费米表面。

在计算出一组特定布里渊区（即在晶体的某一给定方向）的费米级后，可以绘制在布里渊区图上（见图6.19）。若是位于该区的中间部分，则最上端的电子遵循E∝k²规律变化，具有类自由电子的性质（当然，尽管只有最上面的电子具有这种性质），作为金属材料处理。这就是为什么把“自由电子气”认同为金属态的道理。

如果费米面位于该区顶端，或带隙内某处，则最上端的电子不可能移离满带区，除非为它们提供足够大的能量（加热或其他方法）使其跳过能隙而进入下一能级。如跳入下一能级，就会留下带正电荷的穴。正如前面章节所介绍，由于其代表缺少具有负有效质量的电子，所以具有正的质量。

最后，讨论本征半导体中费米级的实际位置。由式（6.23）注意到，费米级的位置与态密度函数Z（E）有关，不同材料是不一样的，在固体能带隙中为零。记住，该函数并不能表述电子的实际分布，只表示适合它们的能态。根据现有态及费米-狄拉克分布（即在这些态中的分布条件）决定费米级的位置。在半导体或绝缘体中，当绝对温度为零时，价电子带是满的，传导带是空的。显然，费米级位于这些带间间隙的某个位置，该位置取决于传导带中现有空态及价电子带中的满态。下面介绍的简单计算可以帮助理解这种思想的实质，也能够粗略确定费米级的位置。

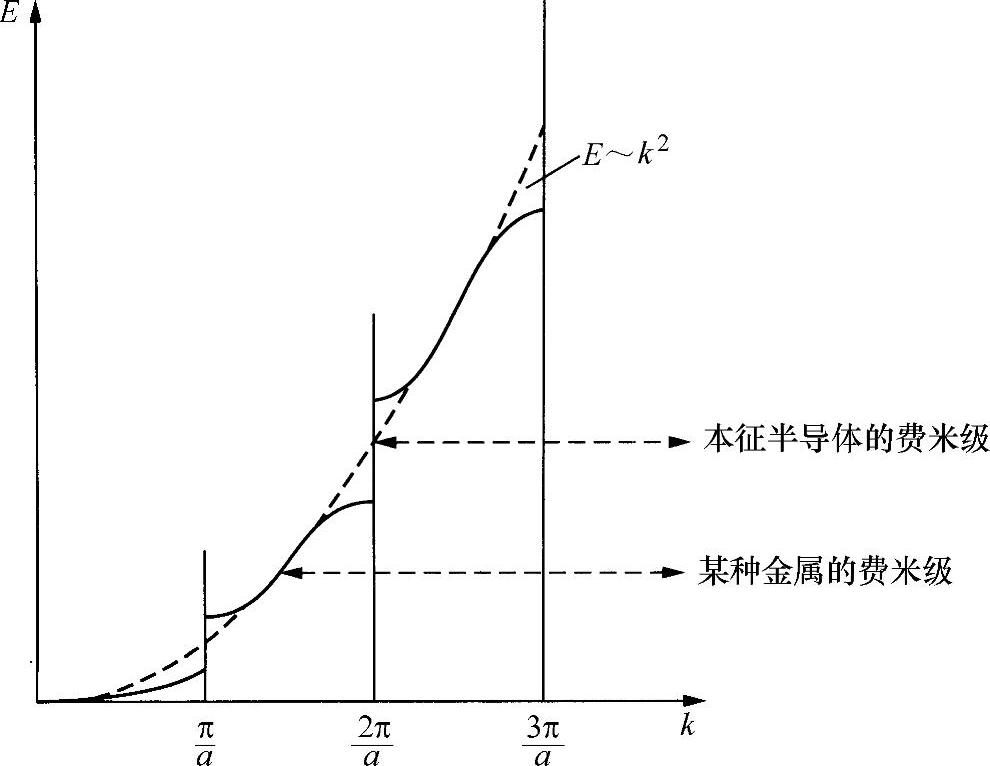
图6.19　布里渊区图上的费米级

假设，价电子带和传导带的宽度相等，并且与带隙相比很小：假如它们完全分别位于能级E_v和E_c上（见图6.20），且两个能带的态密度相等，并等于Z。在此条件下，就给出两种电子密度：

价电子带

传导带

图6.20　简化的某半导体的能级图

当然，随着温度升高，某些电子能够从价电子带，经过费米-狄拉克“尾部”，跳到传导带。但是，在绝对零度，如果价电子带是满的，传导带是空的，则该系统内（单位体积内）的电子总数恰好等于价电子带中可用态的数目Z。在其他温度下，传导带中无论什么电子都必须源自价电子带，以便使(www.xing528.com)

n_v+n_c=Z

利用式（6.24a）和式（6.24b），得

换句话说，费米级精确位于价电子带与传导带的中间位置。这种近似表达式相当好，但是，由于跃升到传导带的电子具有的有效质量要比位于价电子带顶部时（因而有更大机动性）质量小，所以，与价电子带相比，费米级实际上更靠近传导带（即稍微有些上升）。

前面所述的所有内容就是说：由于电子分布的尾部要以费米级为对称，并且传导带中的电子一定源自价电子带，因此在价电子带中会留下等量的穴；费米级一定相对于两种带对称分布（一定位于两带之间的中间位置）。

正如所预测的，半导体中费米级有几种不同位置，对应着不同的性质和结果，电子能量分布的详细内容可参考本书附录X。

本书附录X还推导出了精确结果，给出了下列形式的半导体费米能量值：

式中，p和n分别代表价电子带中穴和传导带中电子的浓度。

对于一直讨论的本征半导体材料，价电子带中的穴是将电子热激励到传导带而获得的，因此有：

n=p=n_i　（假设） （6.27a）

因此

np=n²_i （6.27b）

n_i称为本征载体密度，对于给定温度下的某种材料是个常数。

由于式（6.27b）代表带中穴和电子两者之间的一种平衡，所以总是正确的。无论电子和穴如何形成都是正确的。因此，对于非本征半导体（参考下一节），与本征半导体一样是正确的。对于非本征情况，有：

np=n²_i　n≠p

本书附录X对这些内容都有精确地阐述。

现在可以得出结论：对于本征半导体，有p=n，则式（6.26）中第二项为零，因此式（6.25）和式（6.26）的惟一差别就是m^∗_e与m^∗_h间的差别；如果它们相等，式（6.26）中的第三项也是零，两个公式一样。然而，在本章6.3.3节已经看到，由于两类载体在各自的布里渊区边缘有不同的迁移率，所以m^∗_h>m^∗_e，ln（m^∗_e/m^∗_h）是负值，并且费米级稍微向上偏移，从带隙中点移向传导带，使更多活动电子对材料的电导率有更大贡献。

现在，继续将这些思想应用于“掺杂”半导体或者“非本征”半导体。