布里渊区边缘的有效电子质量变化

首先，需要确定具有带结构的固体的态密度。式（6.16a）和式（6.16b）代表“电子气体”中完全不受约束的电子的态密度函数。而在固体材料中，晶格结构以禁能带（简称禁带）的形式施以非常严重的“约束”，所以该情况下的计算会更为复杂。

在确定了态密度函数后，再次利用费米-狄拉克分布推导出实际的电子能量分布，所有的物理性质都取决于此分布。

若是自由电子，由下式将能量与波数联系在一起：

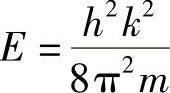
但是，对于约束在带结构内的电子，该式不再成立。显然，由于上述表达式中E是k的连续函数，并且这种带结构会阻止一定的能量，所以该式不可能是正确的。

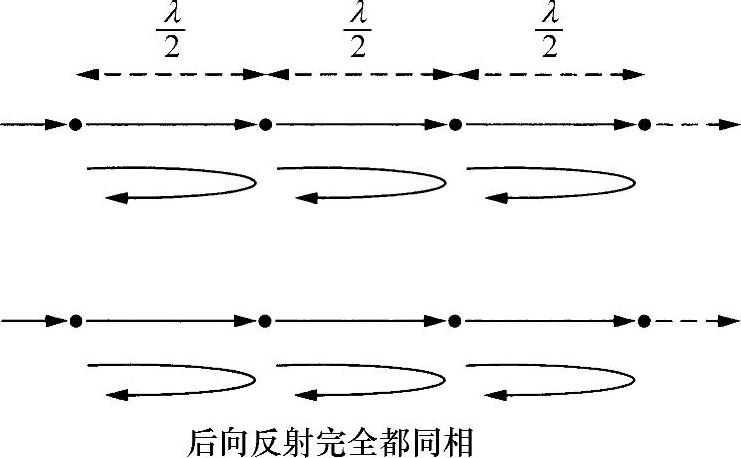
图6.15　禁带布拉格反射的示意图

禁带可以看作是由布拉格（Bragg）反射造成的（由这些电子的反射造成，半波长的整数倍等于晶格间隔）。在这种情况中，由原子向后反射的波都是同相（见图6.15），因而得到相当程度的加强。这意味着前向传播的电子波有着严重反射，不会很容易地向前传播，为此必须遵守的条件为

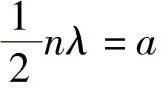
即

式中，a为晶格间隔；n为正或负整数。

实际上，发生上述现象的原因是，晶格内原子所形成的电势阱对满足式（6.20）的电子具有最大影响，相互作用的势能会改变其动能。前向传播波的能量减小，后向传播波的能量增大，在与条件式（6.20）精确对应的波数处会有一个间隙，对波数接近满足式（6.20）的电子也会受到某种程度的影响，其波数偏离nπ/a中的值越大，影响就越小。对一个具体的能量带，其结果是，电子能量是随波数周期性变化（见图6.16a），周期是2π/a。描述这种现象的另外一种方式：无论何时波数增加2π/a，由于后向散射子波之间的相位关系循环重复，因此能量相同，实际上电子波与晶格之间的关系基本上是一样的。所以，通过一个周期内的变化，即-π/a～+π/a内的变化，就完全可以表示E与k之间的关系（见图6.16b）。注意到，该变化近似于自由空间在带的中间点附近的变化（E/k²），但接近边缘处，会有明显偏离。

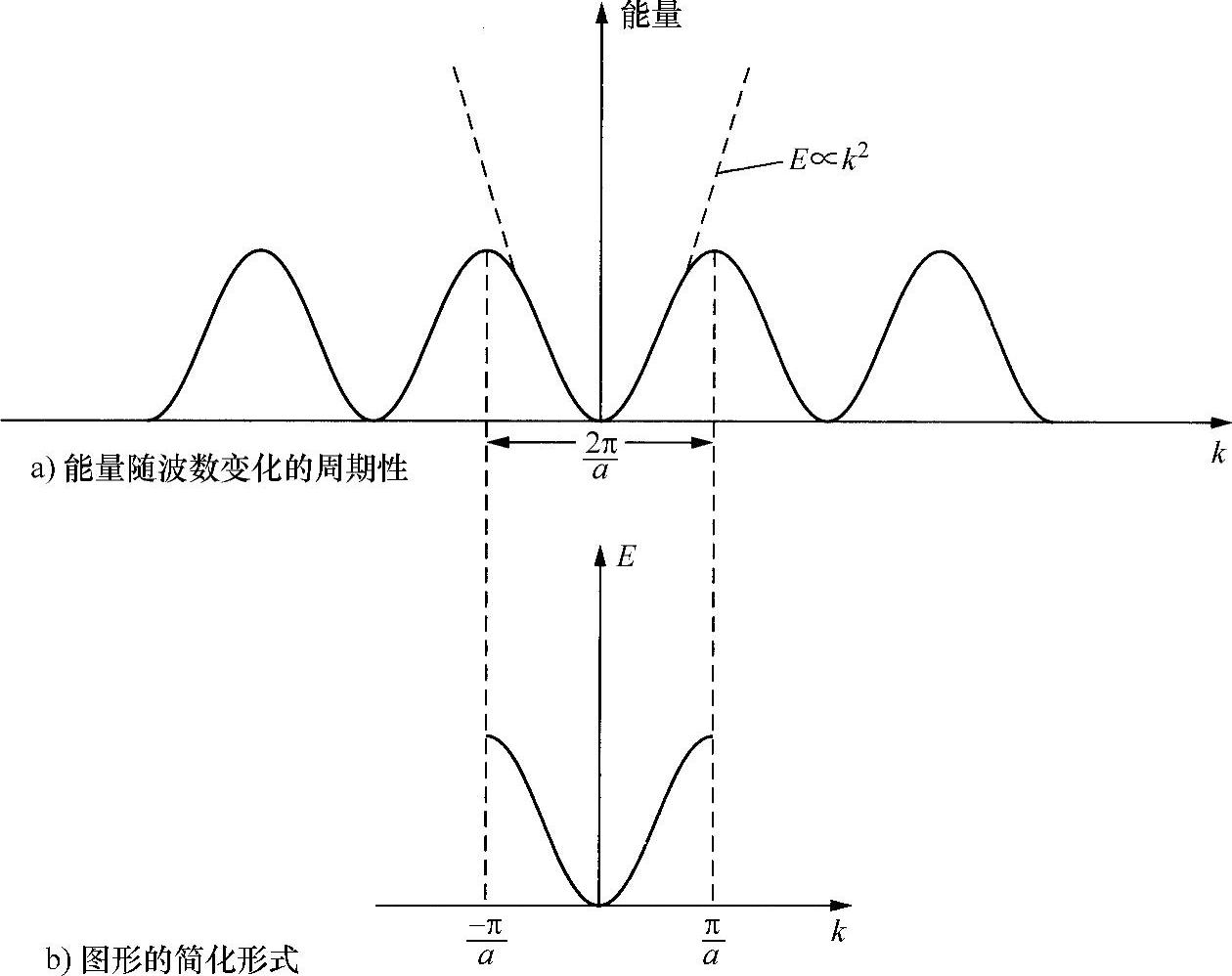
图6.16　晶格低带中的能量和波数

对于下一个较高电子带，结论同样适用。由于远离核子，所以电子有较大势能。像研究第一个带一样，用同样思路讨论其动能，因此，总能量仍然随k周期性变化，周期也是2π/a。由此可以得出结论：所有能带的E/k随k的变化范围都可以限制在-π/a～+π/a的范围内，如图6.17b所示。该图称为“约化布里渊区（reduced Brillouinzone）”图，每个能带称为布里渊区。布里渊区图有一些重要的物理结论，其中一个涉及布里渊区边缘处电子的有效质量。为了理解有效电子的质量变化，再次讨论下面给出的自由电子波数与能量之间的关系：

(www.xing528.com)

如图6.17b所示，在布里渊区边缘，会有比较大的偏离。由此会得出什么结论呢？众所周知，h是基本常数，k是独立变量，所以一定是质量m造成了偏离。对式（6.21）两次微分可以消除独立变量，即

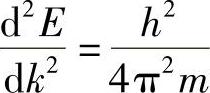
或

式中，m^∗为“有效质量”。在布里渊区边缘附近（见图6.17a），只要d²E/dk²与自由电子不同，该数值就与自由电子不一样。事实上，在布里渊区边缘，d²E/dk²非常小，并且是负的，m∗就变成很大的负值，因此很难移动这个非常大的质量。正如在本书6.3.2节定量分析中看到的，该带上端附近的电子对电导率的贡献接近于零（没有适合于移动的能量，所以不可能产生移动）。

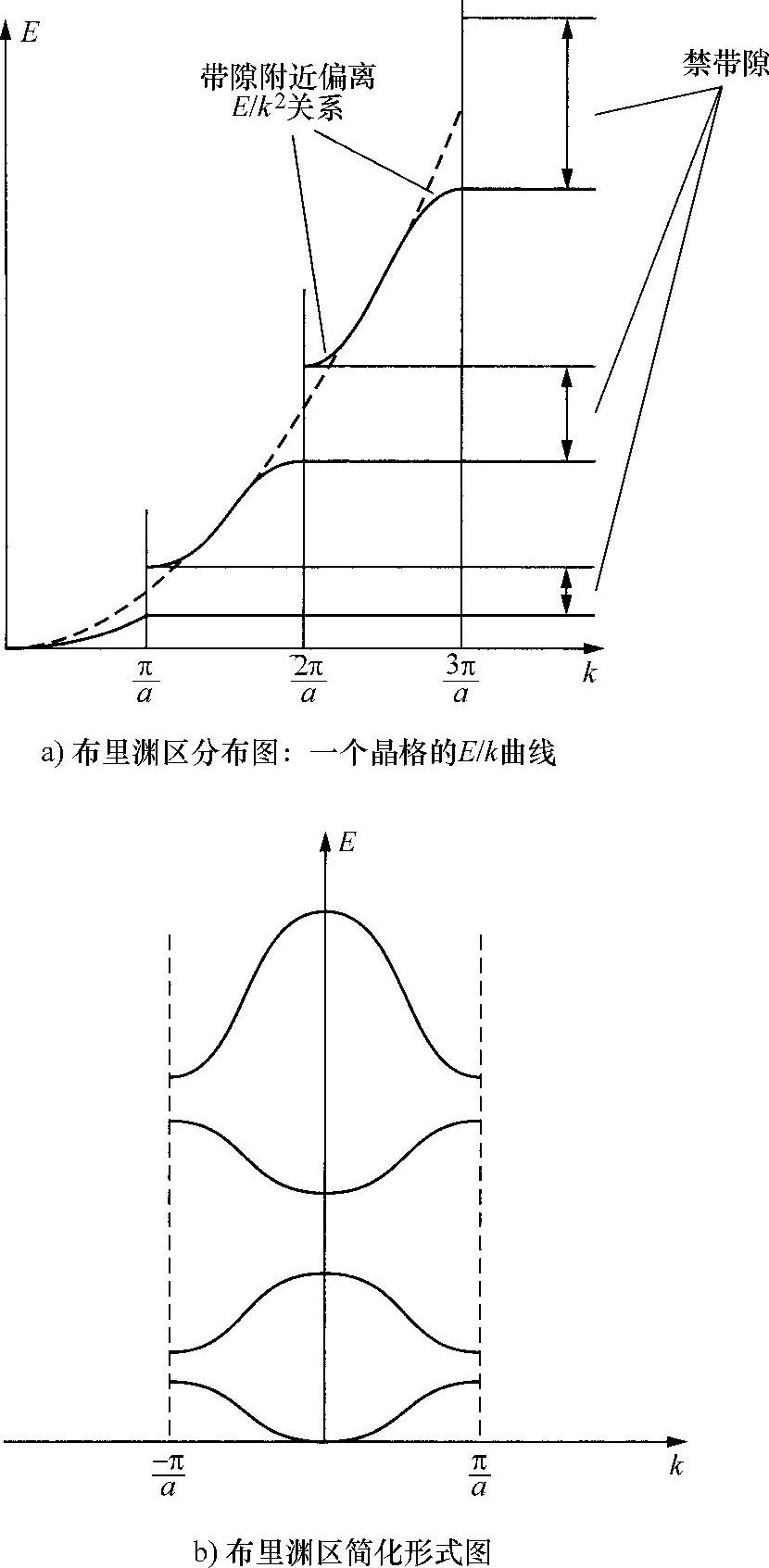
图6.17　固体晶格的布里渊区图

此外，对于带隙较小的情况，如果能够设法使这种电子跳到传导层，就会留下一个没有负电荷和负质量的穴（就是说，该穴带有正电荷，具有正质量）。其依据是，在研究各种半导体的情况时，将这些穴完全想象成带正电荷的粒子非常方便，也非常实际。

反之，在布里渊区下边缘附近，有效质量小，并且是正的，所以该处的电子很容易对电场响应。由此可以得出结论：任何能够从价电子带顶端跳到传导带低端的电子，一旦到达那里，就会具有大的迁移率，因而对材料的电导率会有大的贡献，它们留下的穴对电导率也有贡献，但由于有效质量大，所以贡献量有限。这些就是半导体特性的基本思想。

事实上，在固态理论中，对上述相当频繁使用的术语“迁移率”是有严格定义的，并且在计算相关的半导体性质时相当有用。如果将电场E施加在固体中的一个载荷子上，该载体就会有一个力Ee，因而有一个加速度，即

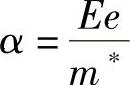
如果该载体在原子碰撞之间的平均时间是τ_c，则根据上式，在时间τ_c内得到的速度就为

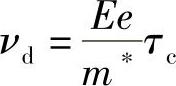
这就是漂移速度，单位电场时的值为

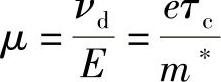
此即迁移率。显然，这是半导体的一个性质，且反比于有效质量m∗，也就是前面章节中使用的含义。