固体能带理论要点解析

理解了固体中会形成能带的原因后，还必须了解电子占据能带的方式，如同理解固体的光子性质时要了解能带本身的形成一样重要。

首先要记住，电子遵守量子理论。与每个电子相关的是一个波（见本书1.8节），其波数（约等于波长的倒数）与电子的动量p有关。

如果电子自由传播，则有下面关系式：

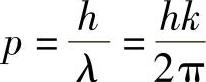
可以用下式将质量为m的粒子的动能与其动量联系在一起：

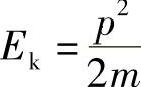
所以，对于自由电子，则有

马上就要用该公式。

电子具有量子特性的另一个结果是，其以一种相当特殊的方式沿合适的能级进行分布，遵守费米-狄拉克（Fermi-Dirac）统计法则。尽管不必对此进行深入探讨，但必须理解基本思想。

所有的基本粒子，如电子、光子、中子、介子和夸克等，都是不可再分的粒子。无法可以在某时或某位置对一个电子进行标记，因此有可能将其认作是处于另一时刻或位置的同一粒子。这不仅仅是“标记”问题，而且是相当基本的量子物理学问题。因此，如果两个相同的（不可分辨的）粒子在系统的能量分布中可以相互交换，那么，就系统的宏观可观察性质来说，就没有任何变化。这些可以观察到的性质仅取决于系统具有的、由所有单个电子波函数组成的总波函数模数的二次方（见本书1.8节）。所有单个电子波函数组成的总波函数为

ψ=ψ（1）ψ（2）…ψ（n）

如果电子1和2可以相互交换，则∣ψ∣²肯定相同，即

∣ψ₁₂∣²=∣ψ₂₁∣²

因此

ψ₁₂=±ψ₂₁

这表示了两种可能性：交换使波函数的符号相同，或者相反。使符号相同的粒子称为对称粒子，反号的粒子称为反对称粒子。

至关重要的是，两个反对称粒子不可能具有同样的量子态。这是因为具有相同量子态的两个相同粒子的交换，不会以任何方式改变波函数，甚至不能改变其符号。因此，两个反对称粒子绝不会有一样的“量子数”。惟一能确定量子态的是量子数，这就是泡利不相容原理（pauli exclusion principle）。电子是反对称粒子，因此遵守泡利不相容原理。事实上，所有具有“半自旋”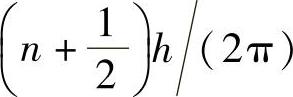的粒子（即电子、光子、中子和μ介子）都遵守该原理，这些粒子称为费米子（fermion，注意现在用小写字母f表示）。具有整自旋nh/（2π）的粒子，是对称粒子（即光子、α-粒子和π介子），遵守玻色-爱因斯坦（Bose-Einstein）统计法，这些粒子称为玻色子（boson）。

两个电子不会具有相同量子态的事实意义深远。并且，在固体的光子性质中，这也是电子特性的最重要性质。这就意味着，有效电子渐进地、有组织地从下到上充满可用量子态，如同在一个竖直管（其直径恰好能够一次取出一个球）中装有许多球一样。

现在，较为详细地介绍一下“填充”过程。

系统中每个容许能量级（一般地）都包含一个以上的量子态，包含的能态数称为能级的“简并度（degeneracy）”。（还要记住，固态能级结构中每个能带是由大量的密集能级组成的，所以在能带中还有一种多简并度。）

首先，假设一个给定能带中的电子完全可以自由移动，仿佛是固体中的电子“气”。这对金属中的电子来说是近似正确的，惟一的限制是电子不能自由地离开固体。如何计算该情况下适合于电子的能态？

在本章6.2.1节，针对产生电磁波的原子振子已经计算过此情况下能量E与E+dE之间的电子数目。一个箱体中的电磁波与电子波非常类似。同电磁波一样，电子波被箱体边界限制到同样一组离散值。惟一的区别是，在电磁情况下要顾及两种偏振态，而在电子情况中必须虑及两个自旋方向。在两种情况中，必须乘以因子2，以便使式（6.6a）仍然成立。也就是说，在k与k+dk之间具有k值的电子态数是g（k），有：

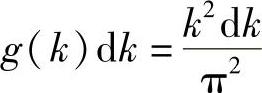
g（k）称为简并函数。现在，必须替换式（6.15）中的k和dk，用能量表示该式为

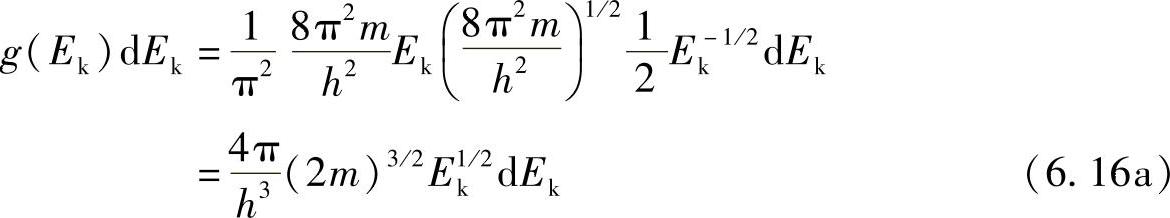
该函数如图6.11所示。对于固态情况，通常称为“态密度”函数，代表能量Ek与E_k+dE_k之间的态数。

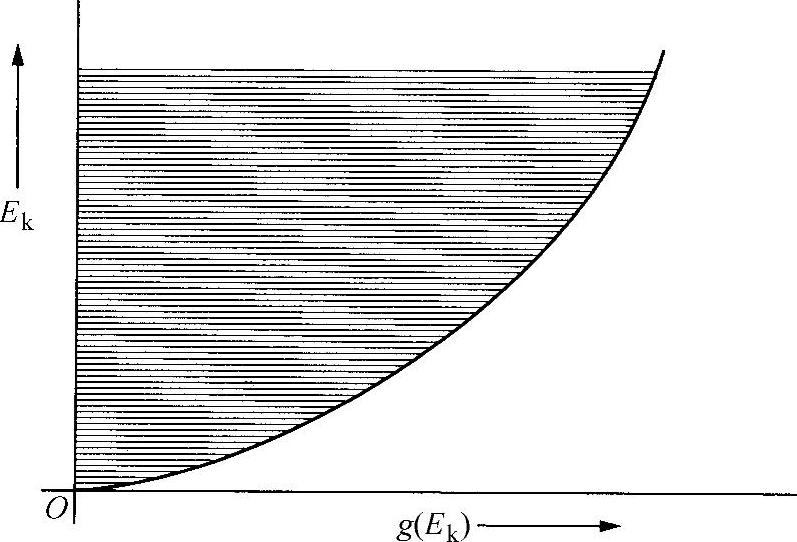
图6.11　某种金属的“态密度”函数

这就是从下至上将要被填充的态，像管中装球一样，E_k～E_k+dE_k的整个范围都要顺序填满。这些态的占有率是多少？电子自身如何在其中精确分布呢？

如果依次填充每个能量区，则最佳表达方式是画出由电子总数N_T充满各g（E_k）能级的函数。若是绝对零度，占有率函数就像图6.12所示的变量A，所有态都被填满，直至电子耗尽。因此，到该能级为止，占有率都是1；高于该能级的，占有率为零。该能级称为费米级E_F。并且，若已知电子总数N_T，很容易计算出E_F，只需对式（6.16a）在0～E_F上积分：

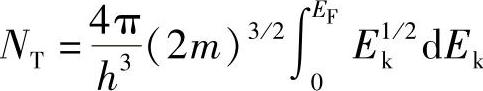(www.xing528.com)

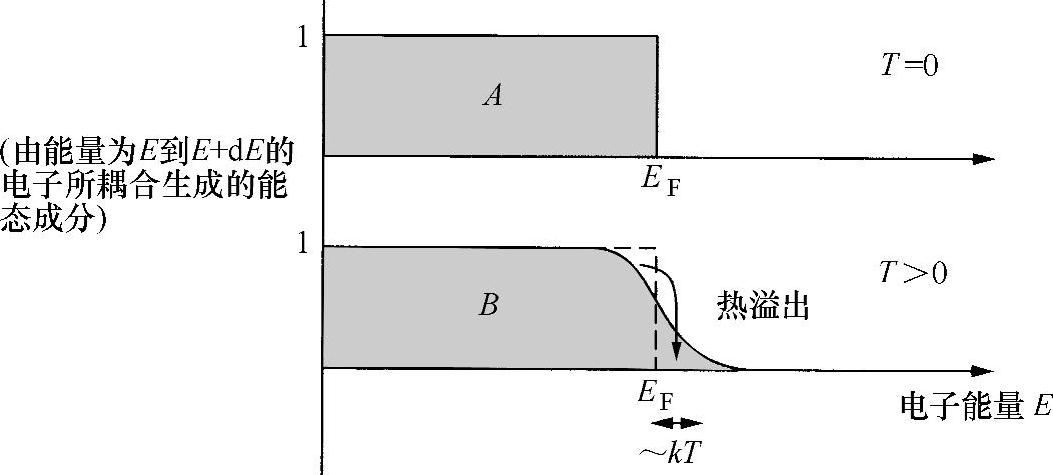
图6.12　费米-狄拉克“占有率”分布

因此有

利用式（6.17），可以很方便地以下面形式表示式（6.16a）所示的态密度函数：

假设，温度稍高于绝对零度，令其为T（>0），就使每个电子额外具有能量约kT（<<E_F）。然而，由于下一个可用的空能级远比kT高，因而大部分电子不能利用这种优势。能够获得能量的只有位于顶层的那些电子，因为在其上面还有空态。因此当温度为T时，该分布就变为1，如图6.12所示B。所以，电子的性质完全不同于气体的情况。在气体中，所有分子的平均能量都会增加kT（原因是，金属的比热要比根据金属导电的自由电子理论预测的值小得多（约为1%），这种差异使20世纪早期的物理学家感到非常迷惑。）

描述某给定温度下能级占有率的函数称为费米-狄拉克（Fermi-Dirac）函数，已经在本书附录Ⅶ中完整推导出，由下式给出：

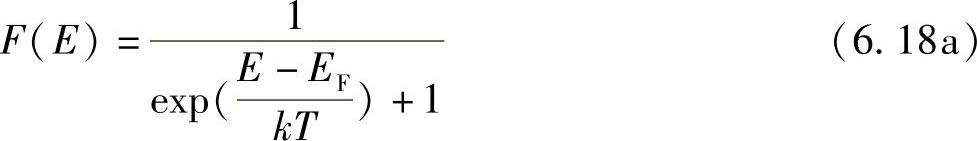
注意到，该式具有已阐述过的性质。

若T=0，并且E<E_F，则

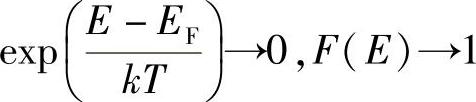
若T=0，并且E>E_F，则

很清楚地，这对应图6.12所示的A。

随着温度升高，最高层电子移动到较高态，该函数扩展出一个宽度约为kT的“尾部”（图6.12所示的B）。此情况下，能量E_F对应着F（E）=0.5时的能量。

现在讨论最后步骤：一个给定的小能量范围内的电子密度是量子态密度与其实际占有率的乘积，也是态密度函数式（6.16b）与费米-狄拉克函数式（6.18a）的乘积，即n（E）dE=g（E）F（E）dE，或

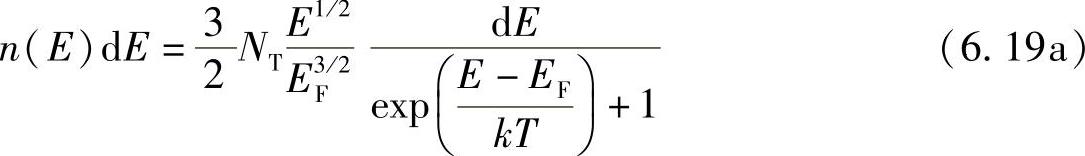
式中，n（E）dE代表E～E+dE能量范围内单位体积的电子数，该函数如图6.13所示。图中分别给出了T=0和T≠0的情况。

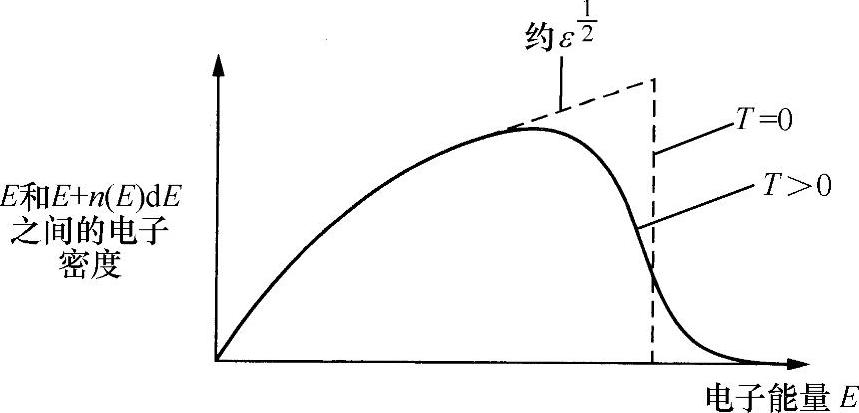
图6.13　某种金属的电子密度分布

在结束讨论之前，很高兴注意到，费米-狄拉克分布实际上是一个普遍的性质，因为固体中的电子数目与量子态的数目相差不多，所以，根据量子论原则，必须仔细地挑选电子。如果量子态的数目远远超过同一粒子的数目，如同气体中一样，量子论原则就几乎不明显了。为了说明这一点，假设式（6.16b）中g（E）>>N_T，则E^1/2>>E^3/2_F，因此式（6.19a）就变为

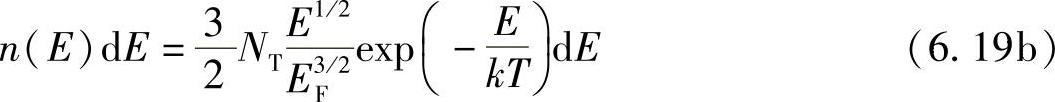
用分子速度ν表示，并且这种情况下的分子能量是其运动动能，就是说

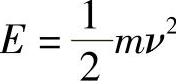
则

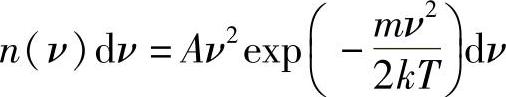
这是从经典（即非量子论）统计热力学演绎出的麦克斯韦-玻耳兹曼（Maxwell-Boltzmann）气体速度的分布公式（见参考文献[1]）。

在固态物理中，式（6.19b）也是一个有用的近似表达式。当电子分布发生在高于费米能级之上的所有情况中（即E>>E_F），式（6.18a）的费米-狄拉克分布函数可以近似为

当然，这就是玻耳兹曼因子，后面将介绍利用该公式的几个例子。