光子学设计基础：速率方程与增益机理

本书4.4.2节已经介绍过激光工作的基本要素。正如已经强调过的，激光在光子学中特别重要，必须更加详细地定量阐述激光的作用。

现在，考虑原子系统有两个能级E₁和E₂的情况，其中E₂>E₁（见图6.3）。

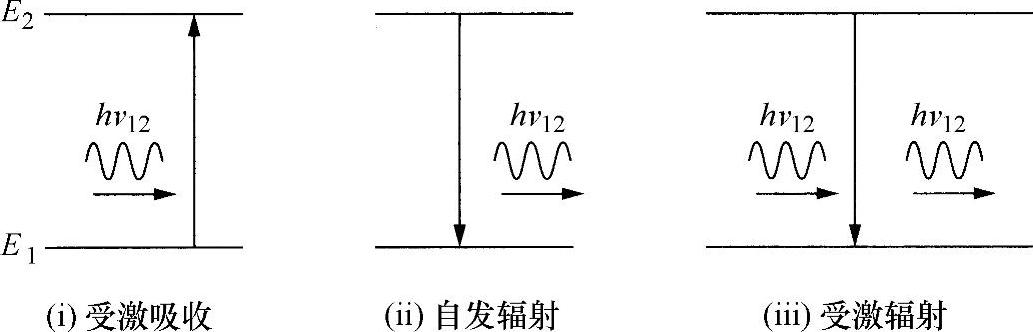
图6.3　两级光子跃迁

已经知道，通过吸收一个频率为ν₁₂的光子，可以使系统从E₁跃升到E₂，有：

hν₁₂=E₂-E₁

激励后，该系统会最终通过发射一个能量为hν₁₂的光子而本能地恢复到基态E₁。

然而，在本书4.4.2节介绍过，受激态E₂在另一个能量为hν₁₂的光子作用下也可以衰变到E₁态，该过程称为受激发射。现在，讨论三种截然不同的过程：

（a）受激吸收（E₁→E₂）

（b）自发辐射（E₂→E₁）

（c）受激辐射（E₂→E₁）

由于违反能量守恒，所以没有“自发吸收”。

为了计算平衡状态下原子与辐射（即黑体辐射）间的关系，爱因斯坦（Einstein）采用一种很简单的论点：将原子看作彼此处于平衡，并在一个密闭系统中进行辐射。将原子升迁到较高态的速率正比于能量为hν₁₂时的光子密度ρ_ν和能态E₁时的原子密度N₁（单位体积内的数目），即

R₁₂=N₁ρ_νB₁₂　（受激吸收）

式中，B₁₂为常数。

同样，处于能态E₂的原子被激励回复到能态E₁的速率为

R₂₁=N₂ρ_νB₂₁ （受激辐射）

式中，N₂为能态E₂下的原子密度。根据详细的原子特性确定特征延迟之后，会出现由能态E₂到能态E₁的自发辐射，并遵守量子理论，其速率简单地正比于比例常数N₂，基本上是由衰变时间的倒数组成，因此有：

S₂₁=N₂A₂₁ （自发辐射）

常数A₂₁、B₁₂和B₂₁称为发射系数。

显然，根据平衡原理，向上和向下的总跃迁速率应当相等，因此，必须有：

N₁ρ_νB₁₂=N₂ρ_νB₂₁+N₂A₂₁ （6.10）

（原文公式右侧将A₂₁错印为A₁₂。——译者注）

由式（6.10），有

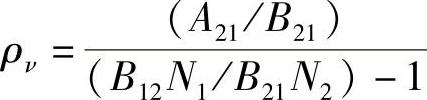
由式（4.13）的玻耳兹曼关系知道

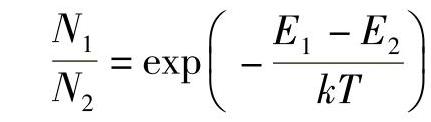
并且

E₂-E₁=hν₁₂

由ν₁₂和ν得到一般性结论：

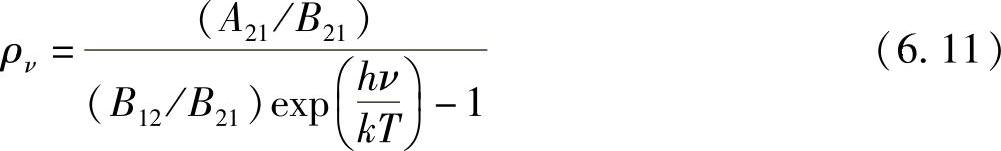
在本书6.2.2节（原文错印为6.2.1节。——译者注）已经阐述过平衡（黑体）辐射（即式（6.8）），有：

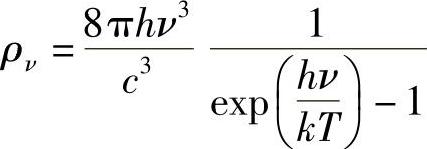
将该表达式与式（6.11）相比较，可以得出：

B₁₂=B₂₁ （6.12a）

式（6.12）称为发射关系式，对确定原子与辐射间的关系非常重要。例如，在这些条件下，从E₂到E₁的受激发射和自发辐射之比为

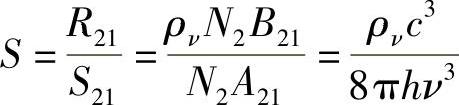
利用表示ρ_ν的式（6.8），则有：

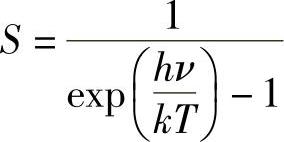
例如，如果讨论一种特定的情况：温度为370K，He-Ne放电，波长λ=632.8nm（ν=4.74×10¹⁴Hz），则得到：

S≈2×10^-27(www.xing528.com)

因此，对于平衡系统来说，受激辐射的可能性很小。

值得注意的另外一点是，如果N₂（高能态E₂时的原子密度）和ρ_ν（光子密度）一定，则受激辐射（B₂₁）的速率就正比于1/ν³。因为有

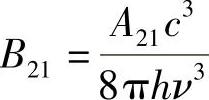
并且，A₂₁是原子常数，等于自发衰变时间的倒数。所以，根据式（6.12b）就可以得出上述结论。

这意味着，频率越高，激光作用就越难。原因取决于受激发射的情况（见本书4.4.2节）。紫外、X射线和γ射线激光有非常特殊的问题，从而阻碍了“死光”武器的发展（X射线和γ射线对活体组织有很强的伤害）。

然而，人们的确希望使用低频激光，如为通信、显示和测量目的使用的可见光和红外光谱范围的激光光束。计算R₂₁的公式表明，增大受激发射的方式是增大N₂和ρ_ν。

由玻耳兹曼因子的形式知道，平衡状态时N₂>N₁，ρ_ν可以由式（6.8）给出，因此，为了得到足够的受激发射所需要的能量，必须破坏这种平衡。

一种方法是输入频率为ν的辐射，以便将ρ_ν增大到高于平衡值。假设，该过程一直持续到受激辐射大大超过自发辐射（当然，自发辐射与ρ_ν无关），就是说直至下式成立：

N₂ρ_νB₂₁>>N₂A₂₁

显然，其条件为

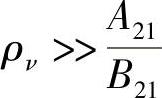
由式（6.12），该式意味着

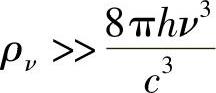
然而，增大ρ_ν也能增大受激吸收。事实上，当ρ_ν较大时，式（6.10）就变为

N₁ρ_νB₁₂=N₂ρ_νB₂₁

但是，由式（6.12）还知道B₁₂=B₂₁，因此在这些条件下N₁=N₂。换句话说，一个频率为ν的输入光子，由于是向上跃迁（受激吸收）的光子，所以有可能造成向下跃迁（受激发射）。不能简单地将更多频率为ν的辐射泵浦到系统中，而使粒子数N₂大于N₁。显然，要增强受激发射并产生激光，必须改变方针和策略。

现在，讨论一个三能级而非二能级的系统（见图6.4a）。假设，将频率为ν₁₃的光入射到该系统，使其从E₁到E₃有大量的受激吸收。从E₃到E₂会有自发衰变，并且E₂→E₁和E₃→E₁也有。根据平衡原则，适当选择这些能级，则E₃→E₂衰变可能快些，而E₂→E₁相对慢很多。显然，其结果是原子聚集在E₂级。与前面阐述的两能级情况不同，该情况的重要之处在于：E₂能级上的原子不会受频率为ν₁₃光子的影响而受激发射，因此，通过增大频率为ν₁₃辐射的强度，可以增加E₂级上的原子数目，但会以减少E₁级上的原子数为代价，由此保证：

N₂>N₁

由于是在频率ν₁₃下泵浦，所以形成“反转粒子数（inverted population）”（高能态比低能态有更多原子），从而可以利用反转粒子数使频率为ν₁₂的光放大。

现在，通过已经得到的速率方程将该放大率量化。假设，使频率为ν₁₂的光子沿某个方向输入到介质内。这将满足E₂能态反转粒子数的要求，激励向下跃迁E₂→E₁，并且在该过程中产生更多频率为ν₁₂的光子（当然，这是放大的起始点）。可以相当肯定地假设，该介质受到受激光子足够强大的泵浦，完全超过从E₂到E₁的自发辐射，在这些条件下再次假设，输入辐射进入系统时单位体积的光子数是p₁₂，增加的速率取决于第一和第二能级间上下跃迁的速率差，因此可以写为

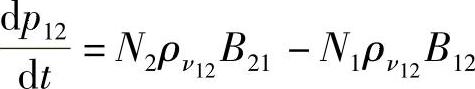
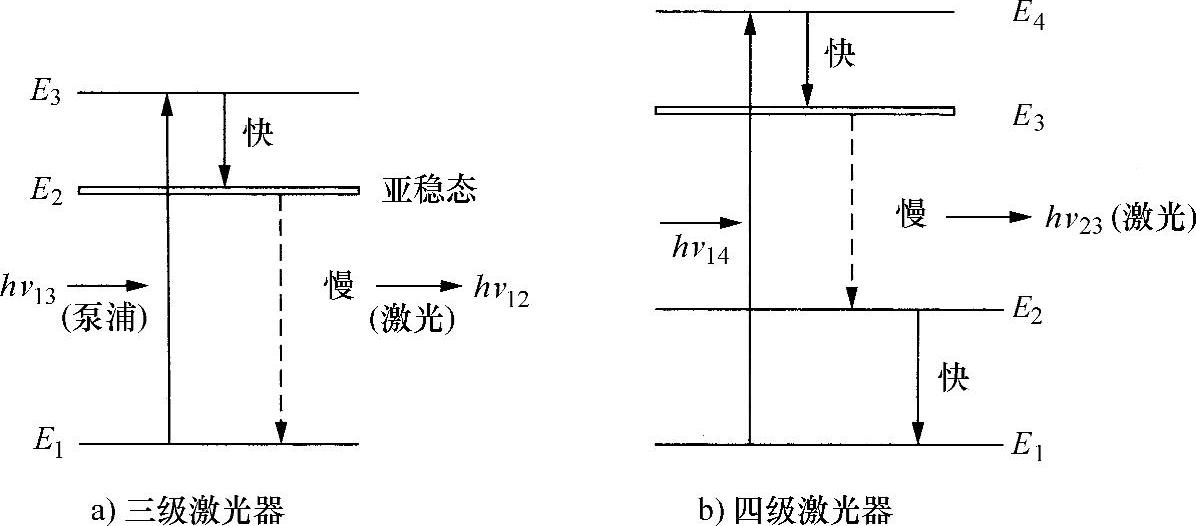
图6.4　激光作用的能级图

式中，ρ_ν12为光子的能量密度，所以有

ρ_ν12=p₁₂hν₁₂

已知B₁₂=B₂₁（由式（6.12）），因此有

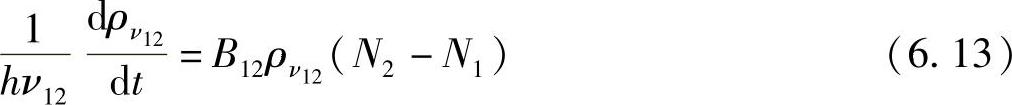
为避免混乱，将ρ_ν12写作ρ_ν，并对式（6.13）积分，有

ρ_ν=ρ_ν，0exp[hνB₁₂（N₂-N₁）t]

式中，t=0时，ρ_ν，0=ρ_ν1。

若输入波以速度c在介质中传播，由s=ct，可以转换成距离参数，得到

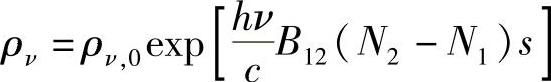
将其与光在相互作用介质中传播所造成的标准损耗/增益相比较。标准损耗/增益为

I=I₀exp（gx）

显然，增益系数g确定为

这是该介质的增益系数（按照单位长度上的强度以分数形式增大）。并且，由于是反转粒子数情况，所以，只要N₂>N₁，增益系数就是正值（是增益而非损耗），这种介质就是一个光学放大器。输入的频率为ν₁₂的辐射就从光学泵浦中接受到下面给出的增益：

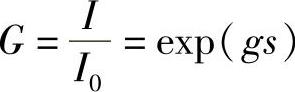
增益是以指数形式随进入介质的距离而增大的。显然，式（6.14a）中的g正比于（N₂-N₁）。对于正在讨论的三级系统，放大跃迁的低能态是基态，初始该能级上的粒子数严重反转。由此可以得出结论：在实现粒子数反转（N₂>N₁）之前，多余一半的原子一定会受到泵浦的激励。利用泵浦激励所有这些原子是相当困难的。现在，讨论图6.4b所示的四级系统。用频率ν₁₄泵浦，会快速地衰变到第三级，以及缓慢地衰变到第二和第一级。之后，会马上再次从第二级衰变到第一级。显然，由于第二级不能首先良好地增加粒子数（但高于基态），并因快速衰变到基态而使原子无法聚集在此，其结果是，比较容易使第三级的反转粒子数多于第二级，因此很容易保证

N₃>>N₂

与三级系统保证N₂>N₁相比，会使用更少的泵浦能量。在ν₃₂时的放大作用更强，因此四级系统非常有利于设计成一个更为有效的放大器。