量子效应、普朗克辐射公式和维恩位移定律

1900年，马克斯·普朗克（Max Planck）发现了一个非常简单、可以避免上述问题的方法。他认为，一个振子不可能具有任意的能量值，只能具有某最小值整数倍的一个值。如果最小值是ε，那么振荡可能具有的能量值就是ε、2ε、3ε、…、nε。正如下面要阐述的，事情完全不一样了。

重新回到式（6.3），计算一个振子的平均能量为

现在，dE等同于ε，并且不趋于零，总保持非零值。

ε是振子发射辐射的最小能量，因此可以说它与量hν一样。其中，ν是发射的最低频率。应当记住，振子可以具有任意能量nhν。其中，n是正整数。（现在，用ν代表频率而非f；读者要记住，现在是讨论量子现象，不是连续的现象；h是量子常数普朗克常数，等于6.626×10^-34J·s。）

若是量子论的情况，则

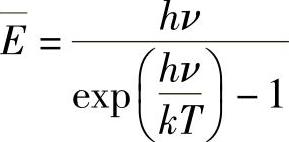
而不再是kT（参考式（6.4）。——译者注）。利用式（6.7），得到ν与ν+dν间的能量密度为

这就是著名的普朗克辐射公式。它解决了前面出现的所有问题，得到了与试验完全相同的光谱（见图6.2）。(www.xing528.com)

如果对所有频率进行积分，仍然是有限积分，得到下面结果：

式（6.9）（原书错印为式（6.2）。——译者注）表示黑体发射总能量的斯忒藩-玻耳兹曼定律（Stefan-Boltzmann）。经典热力学理论能够说明该量正比于绝对温度的四次方，但不能够预测比例常数值，量子物理学对此给出了答案。

同样，经典热力学证明了维恩（Wien）位移定律，认为与光谱（见图6.2）中最大能量相关的波长值反比于绝对温度，即

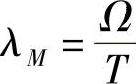
但不能够确定常数Ω的值。对式（6.8）微分，很容易求得

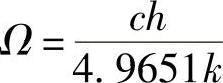
上述结果具有深远影响。尽管普朗克首先认为，量子论假设只是一个为避免紫外灾难而采用的数学窍门，但不久就非常清楚地表明，事实上，这是从根本上阐述了宇宙是如何在运转：量子论诞生了。