黑体辐射的经典推导以及能量谱

倘若物体温度高于绝对零度，则所有物体都将产生辐射。这是因为，温度高于绝对零度意味着原子或分子处于运动状态，因此彼此常发生碰撞，这些碰撞会转移运动的动能，有时将原子系统激励到更高能态，并通过产生光子得到释放，这是物理学中非常基本的原理——“能量守恒定律”。它表示一个系统处于平衡状态时，能量会在所有可能的自由度空间同等分布。材料动能（kinetic energy）是其中一个自由度，激励态（excited state）代表另外一种自由度。若对一个物体施加温度，最终会使其与周围环境处于热平衡状态（即随着时间的流逝，不会从周围环境中获取热量或散失热量），所以一定是能量均分的。

很自然地，产生的第一个问题是，一个具有某给定温度的物体能发射多少辐射？第二个问题（或许不像第一个问题那样自然提出）是，发射的辐射在光谱波长范围内如何分布？

在回答这些问题之前，将阐述一些有益于整个光子学讨论的内容及普通物理学知识，所以花费一些时间和精力是值得的。

经典热力学假设，由于原子内的电子在固有谐振频率下的振荡辐射，使原子发射光。进一步假设（没有必要做其他假设），这些振荡具有任意大小的能量，取决于其刺激强度。

本书4.4.1节已经介绍过，经典热力学所包含的另一个重要内容是玻耳兹曼（Boltzmann）因子。该因子等于绝对温度T时，处于平衡状态下的系统中具有能量E₁的原子数目与具有能量E₂的原子数目之比，并用下式表示：

式中，k为玻耳兹曼常数，值为1.38×10^-23J/K。利用经典热力学知识，通过巧妙选取自变量（没有足够的篇幅阐述该过程，请参阅有关统计力学的内容），已经推导出该因子。

现在，推导由一个“理想”物体发射辐射的经典结果。这个物体是一个能够发射或吸收任何波长辐射的物体，因此包含能以任意频率振荡的振子（原子或分子）。由于是吸收而非反射，所有光都入射其上，所以看起来是“黑色”（至发射之前），这样的物体称为“黑体”。可以根据真实物体接近该黑体的程度进行分类，所以黑体是一个很有意义的理想化物体。

假设，该黑体内有任意能量，并且（通过后面章节的内容会看得更清楚），其能量可以描述成按照下面形式分布的集：

0，dE，2dE，…ndE，…

式中，dE为无限小，以便于分布是连续的。（根据玻耳兹曼因子）具有不同能量带的振子数目之比组成下面形式的集：

如果有N个能量为零的振子，则振子总数为

这是一个很容易相加求和的等比级数，有：

将每一项乘以其配置的能量可以得到所有振子的总能量，即

相加得

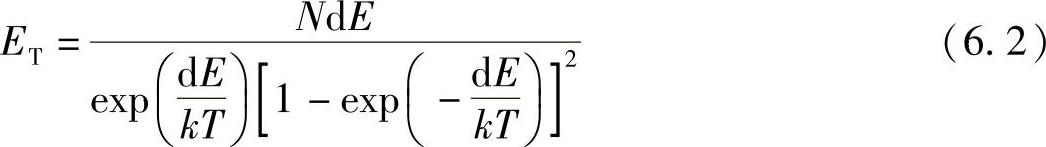
用式（6.2）除以式（6.1），得到每个振子的平均能量为

为了确定上述平均能量的实际价值，使dE→0，可以得到（将分母中的指数展开）：

或

这与其他的“均分”法（允许每个自由度的能量是）完全一致。针对本书介绍的情况，每个振子有两个自由度：其中一个对应动能，另一个对应势能，总计是kT。(www.xing528.com)

需要知道的最后一个内容是，一定体积的材料内可能出现的独立振荡的数目。显然，体积有限意味着具有边界，会对振荡施加边界条件，如同两个固定点之间一条被拉紧的绳子受到约束，绳子的振荡必须使固定点处的振幅为零。

为了使问题简化，假设该材料的体积是边长为l的立方体（见图6.1a）。如果振荡发生在立方体内，并且传播速度是c，那么此振荡情况下施加于立方体侧壁上的边界条件是振幅为零，所以只有与立方体侧面平行的方向才有频率为nc/（2l）的谐振发生。其中，n为正整数，c/（2l）为基频。

当然，光波可以沿许多个方向传播，最好用波矢量k表示某给定波，既显示波的传播方向，也可表明其振幅为2π/λ（λ为波长）。可以将平行于立方体侧面传播的波的频率和波数表示成下面形式：

分别使Ox、Oy和Oz轴平行于立方体侧面，沿三维方向画出一个与式（6.5）中所有k_n相对应的点阵。很容易看出，立方体内的任何振荡都可以用波矢量（由坐标原点到其中一点）表示，该图常称为“k空间”。

现在要问：在波长k～k+dk范围内该立方体能够支撑多少个振荡？可以看出，这与空间图中半径为k～k+dk的球形之间的点数相对应。当然，k空间中的该体积值是4πk²dk（见图6.1b）。然而，由于只有n为正值才成立，所以，只需要该球壳的八分之一部分，所有轴都是正向。为了确定该体积内的点数，将该点阵除以由点的间隔确定的基元体积（即一个边长为π/l的立方体，体积是π³/l³），因此k与k+dk之间的振荡数为

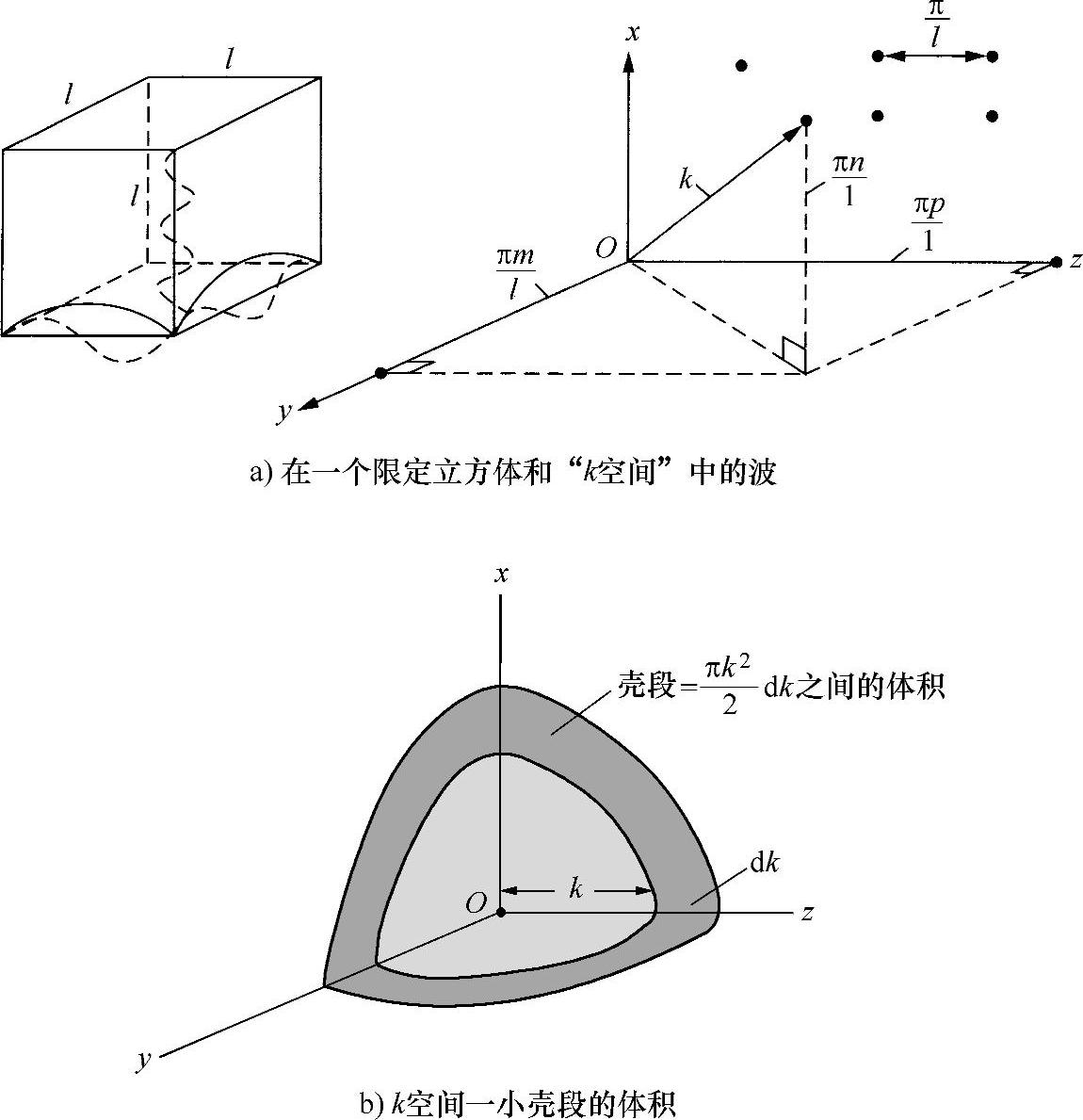
图6.1　k维空间图

如果每个振荡允许有两个正交的线性偏振（由本书第3章知道，一般电磁波都可以分解为这两个分量），上式就变为

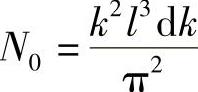
由于开始给出的立方体体积是l³，所以可以用单位体积振荡数的形式表示：

根据频率表示N_ν更为方便（频率与能量的联系更直接）。由于

所以

这是一个非常重要的结果，可应用于激光理论的许多方面，要特别加以注意。

现在，就可以利用它推导经典理论中黑体辐射的能量谱。由式（6.4）看出，每个振荡的平均能量是kT，因此频率f到f+df之间的能量密度（单位体积内的能量）为

这就是经典理论给出的结果，即瑞利-基恩（Rayleigh-Jean）公式。但该公式是完全错误的吗！计算出光谱范围内所有波长发出的总能量密度，可以就立刻明白，即

由此得出的答案：黑体发射出的总能量是无限大，这完全是不可能的。20世纪初，此结果使经典理论物理学家非常挠头。测量出的黑体（结果非常接近实际值）光谱曲线如图6.2所示，低频时与瑞利-基恩表达式（即式（6.7））吻合得非常好，但高频时相差甚多，因此该问题称为“紫外（即高频）灾难”。

图6.2　黑体光谱