光子学设计基础：双光束干涉及其条件

首先，详细研究两束光相干涉的条件（见图5.8）。根据前面对该课题的讨论，很清楚地，当两束波彼此保持一个固定的相位关系就会形成干涉条纹。现在，需要讨论改变互相干度时干涉图的形式。要特别考虑干涉图的“反衬度”，换句话说，就是包括结构和对比度的可测量程度。

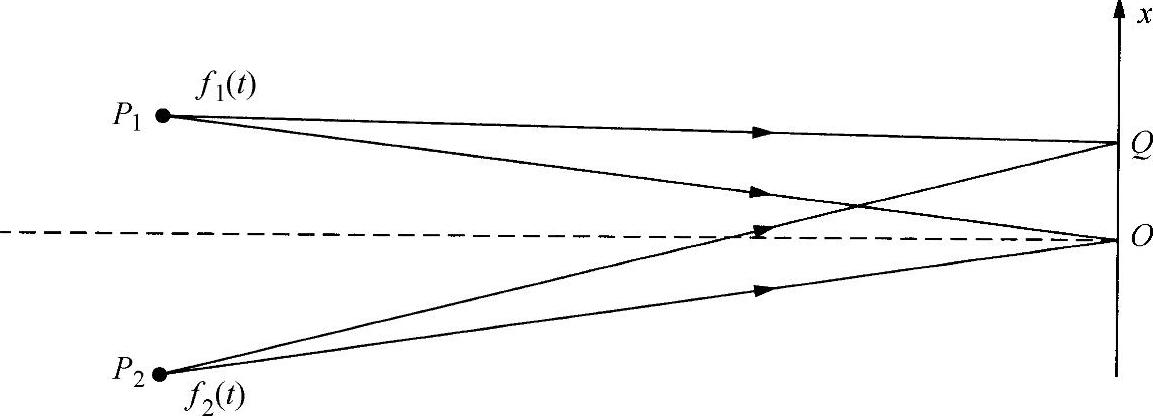
图5.8　两个光源的干涉

两个光源P₁和P₂在点O（见图5.8）产生的（复）振幅为

A=f₁（t″）+f₂（t″）

式中，t″=t′+τ₀；τ₀为光从P₁或P₂传播至点O所需要的时间。如果f₁和f₂是光波的电场振幅，则在点O观察到的光强度是该复数振幅的二次方。记住，复数A=a+ib的模为

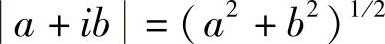
为了得到复数模的二次方，一个非常方便的方法就是乘以其复共轭，即

AA^∗=（a+ib）（a-ib）=（a²+b²）

因此，该种情况下的光强度为

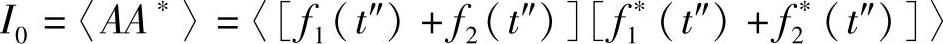
式中，三角括号表示在探测器（人眼）的响应时间内取平均，并假设f₁和f₂含有所需要的比例常数（K^1/2）。比例常数将光强度与电场强度联系在一起（即I=KE²）。

点Q处的振幅为

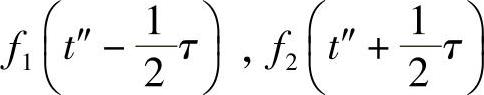
式中，τ为光路P₂Q与P₁Q之间的时间差。

若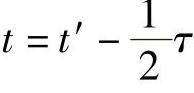，则点Q处的光强度为

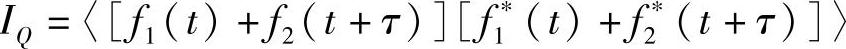
即

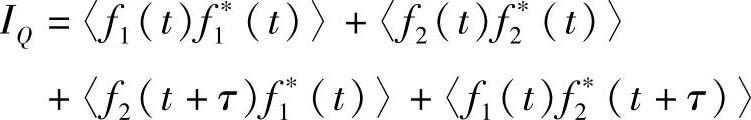
显然，前两项与Q点处两个光源的强度无关，后两项与前面定义的互相关函数一样。事实上有：

<f₁（t）f^∗₂（t+τ）>=c₁₂（τ）

<f^∗₁（t）f₂（t+τ）>=c^∗₁₂（τ）

可能会注意到，如果f₁和f₂是正交偏振，则每一项都是零。因为在该情况下，场振幅在另一个方向上没有分量，因而没有叠加，两束波不可能干涉。因此，其乘积的平均值再次等于平均值的乘积。其中，每一个都是零，并是正弦波。

如果c₁₂（t）是下面形式：

c₁₂（τ）=∣c₁₂（τ）∣exp（iωτ）

（若f₁和f₂是含有ωt的正弦形式时，该式成立），则有

c₁₂（τ）+c^∗₁₂（τ）=2∣c₁₂（τ）∣cosωτ(www.xing528.com)

若在点Q处放置一个探测器接受光强度，其响应时间要比光源的相干时间（自相干时间和互相干时间）长得多（以便使时间平均能够成立），则光强度可以写成下面形式：

I_Q=I₁+I₂+2∣c₁₂（τ）∣cosωt （5.3）

沿x方向移动，会有效地增大τ，则会观察到光强度随振幅2c₁₂（τ）的变化（即互相干函数模的两倍），并在等于两个光强度之和的一个平均值周围变化（见图5.9）。因此，有一个测量光源互相干性c₁₂（τ）的试验方法。

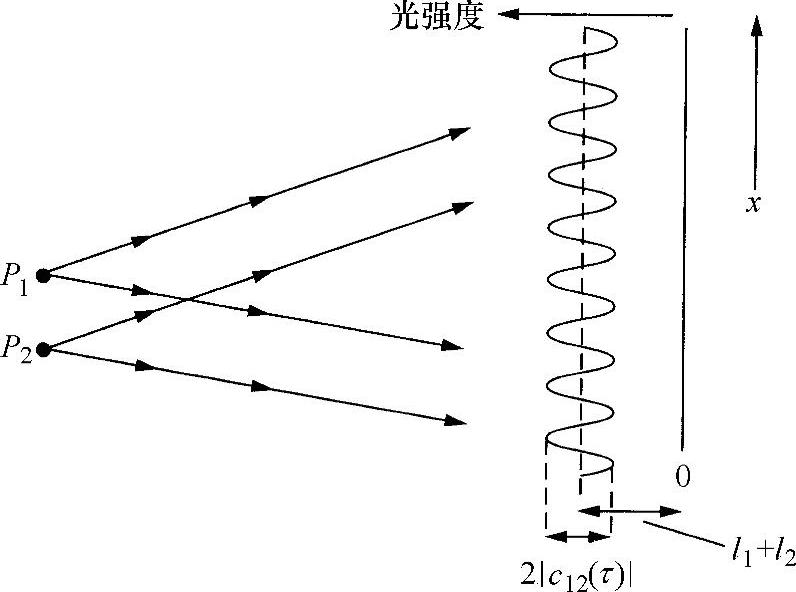
图5.9　双光源干涉图的互相干函数c₁₂（τ）

如果用下式定义该干涉图的条纹清晰度（或反衬度）：

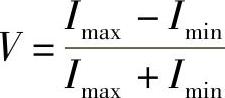
其定量确定了干涉图的对比（即最大与最小值之差是平均值的若干分之一），则由式（5.3）得到

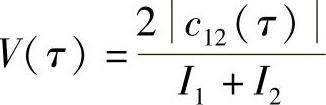
根据前面的定义有

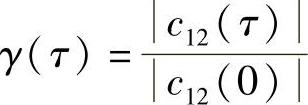
注意到

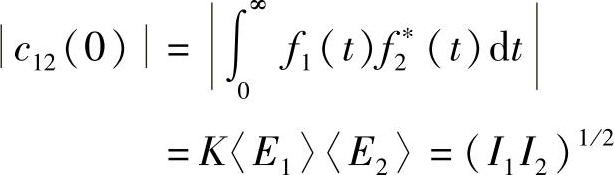
因此

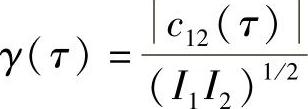
通过下式将反衬度函数V（τ）与相干函数γ（τ）联系在一起：

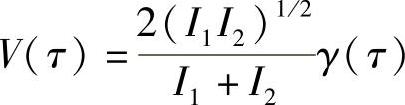
如果两个光强度相等，就有

V（τ）=γ（τ）

就是说，反衬度和相干函数是一样的。

由此得出结论：等光强度相干光源的反衬度是100%（γ=1），非相干光源的反衬度是零；对局部相干光源，反衬度是实际相干性的直接测量。

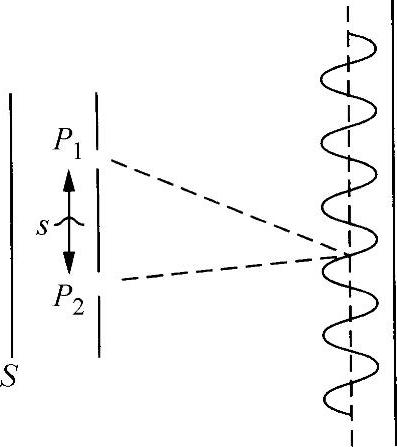
图5.10　扩展光源的干涉

如果P₁和P₂是到照明光源S等距离的两个针孔，显然其反衬度函数就是测量S的自相干性的。此外，根据维纳-辛钦定理，该函数的傅里叶变换就是该光源的功率谱。

假设，两个针孔放置在一个扩展光源的前面，如图5.10所示，其间隔是可变的。这些光源产生的干涉图是对该扩展光源上两个对应点间相关性的测量。如果初始间隔为零，逐渐增大直至反衬度降为零，那么此时的间隔值就确定了扩展光源空间相干性的大小。若光源是各向同性，也相应地确定了相干面积。换句话说，在这种情况下，一个给定的光源点与中心点所照明的圆形区域之外的任何点都没有相位相关性。