【摘要】:维纳-辛钦定理有非常实际的应用价值。该定律认为,函数f的自相关函数c(τ)的傅里叶变换给出f的功率谱,根据傅里叶分析中的卷积定理就可以直接得出。在5.1节介绍过,光谱带宽与相干性密切相关,并且自相关是相干性的一种计量,所以在此不致引起过度惊讶。正如将要了解的,由于可以根据光的干涉性质确定自相关函数,所以维纳-辛钦定理是非常实用的。
维纳-辛钦(Wiener-Khinchin)定理有非常实际的应用价值。
该定律认为,函数f(t)的自相关函数c(τ)的傅里叶变换(Fourier Trans-form,FT)给出f(t)的功率谱,根据傅里叶分析中的卷积定理就可以直接得出。卷积定理是:两个函数卷积的傅里叶变换等于单个傅里叶变换的乘积(参考傅里叶变换理论的有关内容,即参考文献[1])。“卷积”就是一直在讨论的“延迟平均”运算过程,因此有
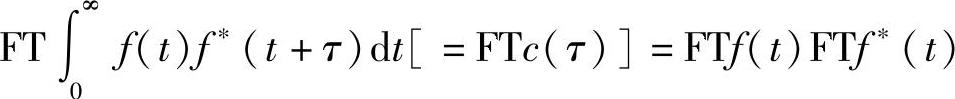
式中,FT为傅里叶变换运算符,若将f(t)写成下面形式:
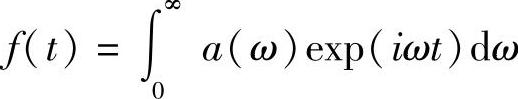
则(https://www.xing528.com)
FTf(t)FTf∗(t)=∣a(ω)∣2
这就是f(t)的“功率”谱,因此可以根据自相关函数确定一个光源的功率谱。在5.1节介绍过,光谱带宽与相干性密切相关,并且自相关是相干性的一种计量,所以在此不致引起过度惊讶。图5.5所示的随机波包流的功率谱如图5.6b所示。
正如将要了解的,由于可以根据光的干涉性质确定(如同所期望的)自相关函数,所以维纳-辛钦定理是非常实用的。这意味着,利用干涉图能够确定光源输出中的频率成分及相关振幅(即整个功率谱)。
为了更清晰地了解实际情况中如何运用这些思想,下面讨论一些具体应用相干理论的例子。
首先,介绍测量光源相干性的一个简单例子。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




