为了确定相干度对光学系统,尤其是包含干涉和衍射现象的光学系统的定量影响,需要定量测量出相干性。如果已知某周期性扰动在某位置和时刻的(复)振幅,就必须判断和预估其在另一位置和时刻的量值。已经知道,纯正弦波有最大值,白光有最小值,将这些值分别定义为1和0是很方便的。
为了诠释这种思想,并使问题简单化,首先讨论纯时间相干性。
可以合理地假设一个时间函数f(t),若已知t时的值,就会知道其后续时刻t′时的值(与时刻t时的值完全无关)。如果两个时间函数完全无关,就希望在一个较长的时间范围内(与其变量(带宽的倒数)的特征时间常数相比),其乘积的平均值等于单个平均值的乘积,即
<f(t)f(t′)>=<f(t)><f(t′)> (5.1)
对绝大多数光学扰动,如果该函数是在零平均值附近振荡,即
<f(t)>=<f(t′)>=0
则由式(5.1)可以得
<f(t)f(t′)>=0
换句话说,当在一个较长时间范围内(与每个时间函数的变化时间相比)平均时,两个独立函数的乘积是零。
另外,若令t=t′,由于以t为变量的时间函数f(t)能够预先给出t时刻的值,所以,上面的“延迟平均值”一定有最大的可能值,因此有
<f(t)f(t′)>=<f2(t)>
并且,一定是“延迟平均值”的最大值。
显然,该乘积的值(对所有真实情况下的函数)从t′=t时的1,下降到t′是其他值时的0。此时,两个变量完全无关。显然,出现这种情况时的t′值越大,依赖性就越强,相干性也就越大。很可能的是,为了测量相干性而寻求的量就是该乘积函数衰变至零时表述速度特征的量。
例如,假设研究一个纯时间正弦函数,已知这是一种理想的相干扰动,因此要求相干测量是1。
将波写成下面形式:
f(t)=asinωt
为了得到“延迟平均”函数,首先将该函数自乘,再用时间τ进行替换(即t′=t+τ)(见图5.3),则有
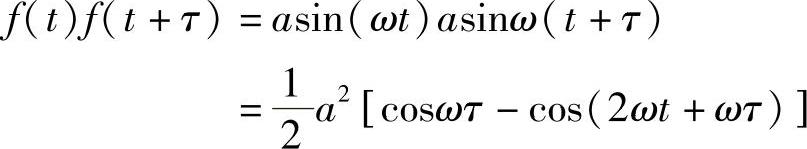
将该式在全部时间范围内进行平均(零带宽对应的特征时间常数为无穷大),由于<cos(2ωt+ωτ)>=0,就有
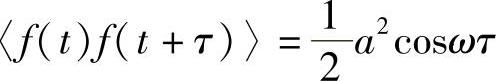
该量称为扰动的自相关函数c(τ)。若按照较规范的数学形式表示,应当是下面计算形式:
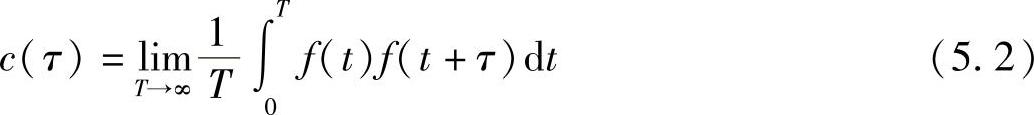
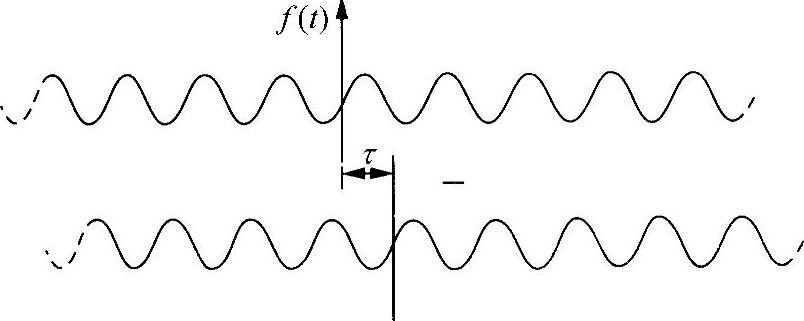
图5.3 自相关延迟
即
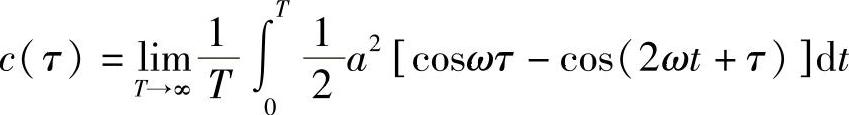
因此
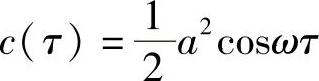
该函数并不衰变,而是随频率ω和固定振幅a2/2振荡。对于振荡场,如光波,总是含有ωτ的正弦项,并且不会提供有用的相干信息,所以就把后面的振幅项作为光波相干性的计量。c(τ)的数学形式称为“卷积”。
由于要求正弦波的相干性计量是1,所以,为了方便,选择将其归化到τ=0时的值(在这种情况下,c(0)=a2/2)。
该规化后的函数称为相干函数γ(τ)。对于所研究的情况,γ(τ)=1(理想相干)。
现在讨论白光。注意到,这等效于一系列随机分布的、有正值也有负值的δ函数(见图5.4)。显然,该系列代表无穷多个频率范围内的光学正弦波散布,每一个的平均振幅值都是零,该系列的平均振幅值也一定是零。如果要得到“延迟平均”函数,就将该组δ函数与一个位移后的δ函数相乘,则只有其中的一部分相叠加。并且,相同符号的两个δ函数的叠加与相反符号的两个δ函数的叠加具有相同的概率。因此,叠加函数的平均值总是零,与时间延迟无关。如此,对于所有的τ,都有c(τ)=0,即γ(τ)=0(即理想非相干)。(https://www.xing528.com)
最后讨论随机量子流或者波包(见图5.5)。
这些波包在传播过程中彼此渗透,并且每个波包自身是相干的。如果这种波包流的波形乘以自身位移后的函数,结果就是图5.6a所示的形式。只有在位移超出一个波包的周期时,相关才基本上降为零。在这种情况下,就会形成一个衰变的正弦波。并且,表征该振幅衰变速率特性的量,就是相干性测量(例如,若是指数衰变情况,时间计算到1/e)。
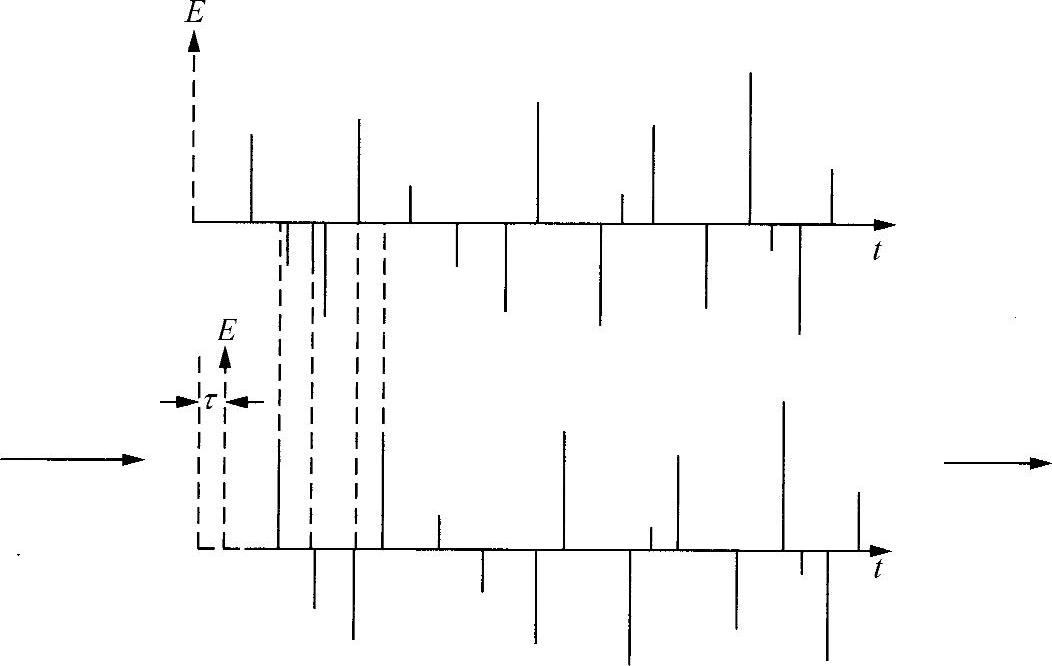
图5.4 随机分布的δ函数的自相关

图5.5 随机波包流
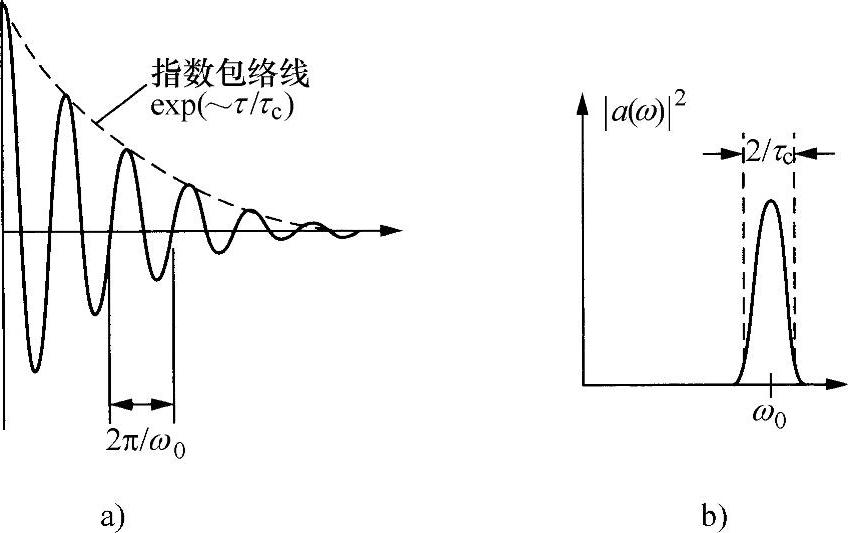
图5.6 波包流相关
一般表达形式的相干函数可以照顾到上述的所有要求,形式如下:
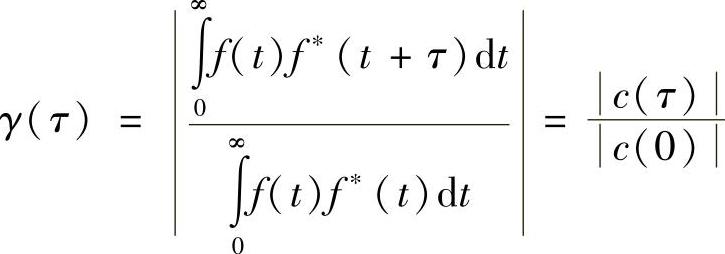
该积分完成了时间平均,利用复数形式可以在一个函数中形成复共轭,以消除复指数表达式中的振荡项;利用模量运算重新使复值变为实值。并且,这种分配方法也影响着所需要的归化。正如式(5.2)定义的,该函数c(τ)称为相关系数,在某些情况下特别有用。注意到,一般情况下,该函数是一个复量。
为了巩固这些知识,现在讨论如何针对纯正弦波运用这些函数。
必须以复指数形式表示正弦波,所以写成下列形式:
f(t)=aexp(iωt)
因此
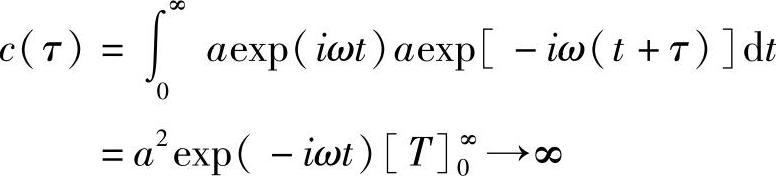
和
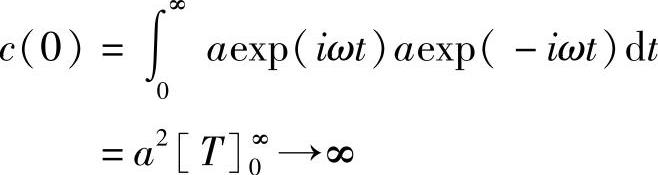
并且
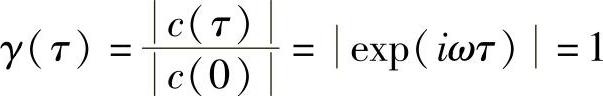
这与所希望的一样。
前面讨论的三种情况的相干函数如图5.7所示。正弦波函数没有衰变,所以其时间相干性无限大;白光函数衰变时间为零,因而相干时间性也是零;波包流函数衰变时间为τc,是局部相干,且相干时间为τc。对所有时间函数,都可以用这种方式定量确定其相干时间。显然,cτc项(c是光速)可以确定相干长度。
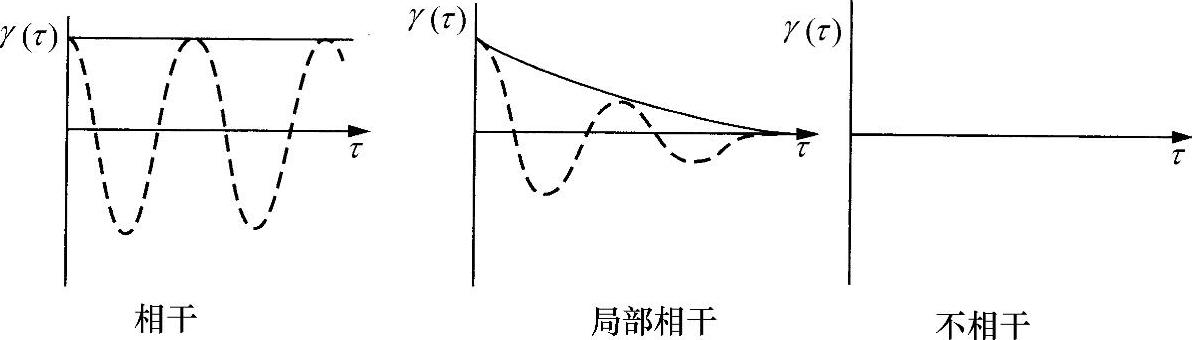
图5.7 相干函数
很明显,可以利用同样思想研究空间相干性,用空间延迟σ代替τ。在这种情况下,可以表示成下列形式:
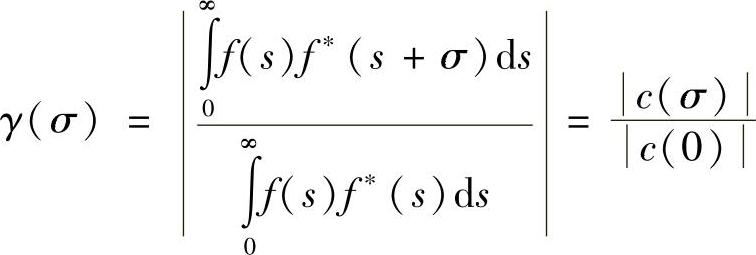
“衰变”参数σc将确定相干长度。
最后,用一个非常类似的互相干函数表示两个独立函数f1(t)和f2(t)的互相干性,即
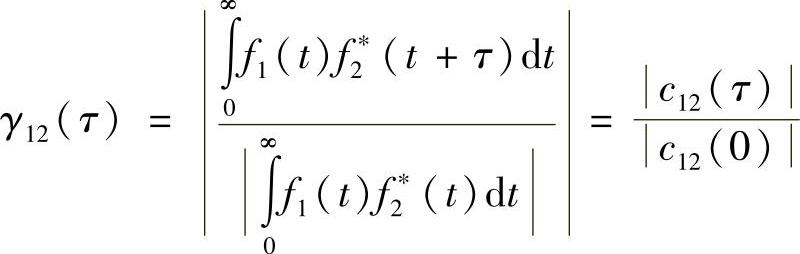
对于互相干情况,分别用s和σ代替t和τ。
有时,γ12称为两个函数间的“相干度”。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




