光探测器设计基础及探测过程分析

能否精确测量光功率的过程，直接取决于光子撞击物质的效应。在大部分定量测量中，该过程取决于使电子升到更高能态级的光子，而直接观察到的则是电流。

应当注意，本节中光子是作为粒子流到达探测器的，到达速率（通常）遵守泊松（Poisson）统计规律。在本书1.7节已经定量讨论过该课题，值得强调的一个重要结果是，光探测过程中的信噪比（SNR）由下式给出：

式中，P_m为平均光学功率；B为光探测器的带宽；h为普朗克常数；ν为光学频率。其重要性在于：测量精度随平均功率的二次方根提高，反比于光学频率的二次方根。原因是，在这两种情况中，当功率P_m较小时，在某一时刻有很少几个光子到达，光子到达过程中“微粒”性质更为明显；当ν较大时，意味着每个光子具有更大能量，因此，若功率一定，在某一时刻仍有很少光子到达。如果探测器是“量子噪声受限”类型（即受到这种到达过程统计性质的限制），式（4.16）的信噪比SNR表达式就是一个至关重要的设计参数。

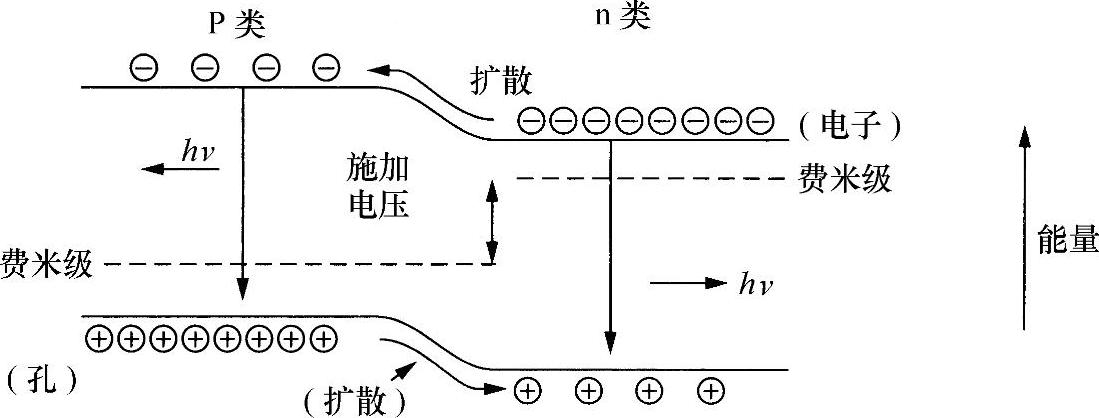
再次讨论图4.9所示的p-n结。在讨论发光时，注意到，这两种半导体（即p和n）间的实际接触会导致主载体通过结进行扩散，企图使两侧的浓度相等。然而，电荷偏振使结两侧形成一个电场。假设，光子入射到暴露于电场一侧的半导体上，若光子有足够能量形成电子-空穴对，这两个新的电荷载体将快速地沿相反方向通过该结，形成可以测量的电流。通过施加“反偏压”电场会使该过程加速。这种简单的过程形成图，有助于确定适合此类装置（称为光敏二极管）的两个重要关系。

(www.xing528.com)

图4.9　发光二极管的能量图

第一，对于产生电子-空穴对的光子，其光学频率ν必须满足hν>E_g。其中，E_g是材料的带隙能量。然而，如果ν太大，所有光子都将被吸收到一个很薄的表面层，该结就不能有效地聚集电荷。每类光敏二极管都有一个频率“响应”光谱，必须与被探测光的光谱相匹配；

第二，假设，希望探测某一光学频率下的光功率P，这意味着每秒有P/（hν）个光子到达。假如，其中有η（百分比）会产生电子-空穴对，则每秒会产生ηP/（hν）个电荷载体（对每种电荷），所以，若所有电荷都被聚集，测量到的电流就是i=eηP/（hν）。

因此，电流正比于光功率。这就意味着，电功率正比于光功率的二次方。所以，若探测过程满足信噪比，重要的是要确定是以电功率还是光功率表示（在表述探测器噪声性能时，这是相当常见的且容易混淆的地方）。

本书第7章将全面讨论光探测器。