光子学设计-光学色散及群速色散

折射率实部随频率变化，这对光波传播有着重要意义。因为这意味着波速随频率变化。所有的真实光源在一定的频率范围内都能发生辐射，对于白炽辐射器，如灯泡，该范围很大；而对于气体激光器，则非常小，但不会是零。因此，对于折射率随频率变化的介质，光源光谱的不同部分将以不同速度传播，具有不同的折射率，从而造成光能量“分散”，这种介质称为“光学色散材料”。

该现象具有一些表现形式和实用的结论。众所周知的一种形式是彩虹，折射率随波长的变化使大气中的雨滴以不同角度折射太阳光，形成不同颜色，因此提供了一种非常重要的五彩图案。另外一种非常熟悉的有关色散的例子，是由艾萨克·牛顿（Isaac Newton）用一块玻璃棱镜完成的。试验定量验证了（太阳光）光谱颜色相对于玻璃具有不同的折射角。

在近代光子学中，更关心的是色散对光束（尤其是导波）携带信息的影响，所以定量确定色散效应是非常有用的。为了理解对色散得出的一些结论，假设光源光谱中恰好含有两个相隔非常近、振幅相等的频率成分：

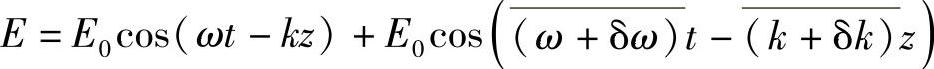
与ω和k相比，式中δω和δk都是小量。

利用初级三角学知识：

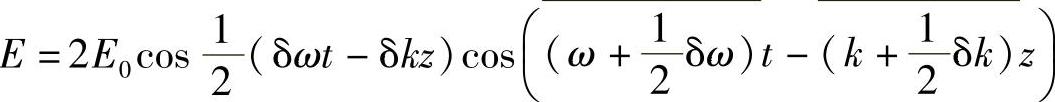
该式代表一个振幅受到具有较低频率的另一个正弦波（第一个因子）调制的正弦波（第二个因子）（见图4.4）。该波以下面速度传播：

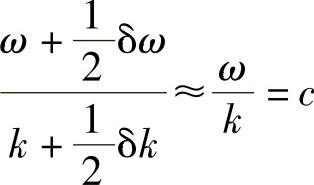
这是两种波的平均速度。然而，当振幅调制具有最大值时，即

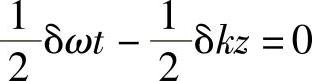
即

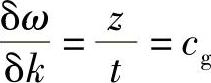
该波就会出现最大振幅点。因此，在δω、δk→0的极限情况下，有：

式中，c_g称为群速，是（这种情况下）任何给定波传播速度的最大值。

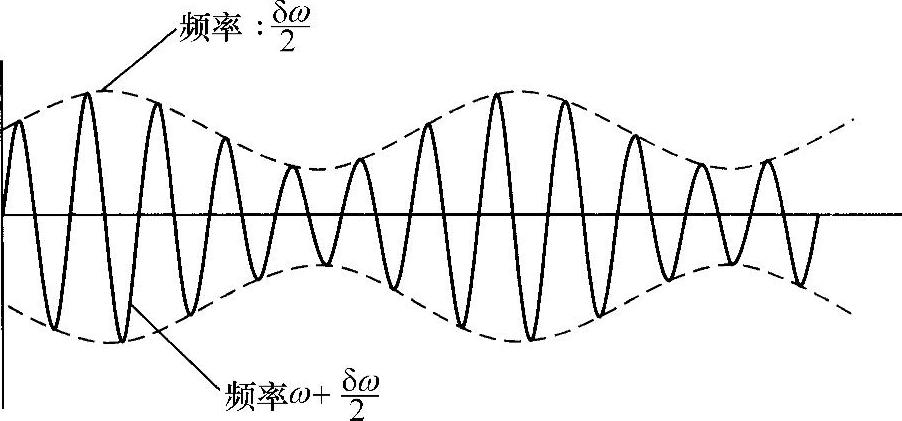
图4.4　振幅得到调制的波：两种不同频率波的和

还知道

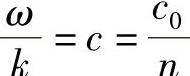
因此，ω=（c₀/n）/k。式中，n是介质的折射率。

一般地，n随光学频率变化，是k的函数，对该表达式微分得

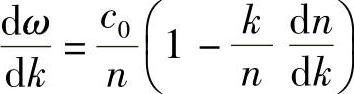(www.xing528.com)

或者，对波长λ微分得

若n不随波长变化，则

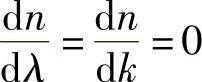
和

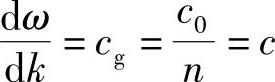
然而，如果dn/dλ≠0（介质是色散材料），则c_g≠c，该扰动的最大值就以不同于“载体”光波的速度传播。这种思想已经在一个实际光源的整个光谱范围内实现。倘若dn/dλ在某些波长的光谱范围内明显地固定不变，可以得出结论：光源发出的一个光脉冲将有效地、无畸变地以速度c_g而非c传播，c_g称为该脉冲的群速。为了方便，将“群折射率”定义为

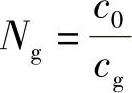
如果dn/dλ<<λ/n（即色散很小），由式（4.10）有：

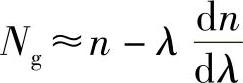
然而，假设dn/dλ在光源光谱范围内不是常数，脉冲的不同部分将以不同的群速传播，所以脉冲宽度会随传播而加宽。若群速c_g一定，通过下式计算出在距离L范围内的传播时间就会看得很清楚，即

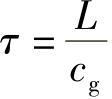
在频率ωδ散布范围内，该变化由下式给出：

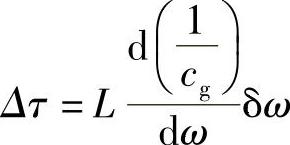
代换式（4.9）中的c_g，有

利用式（4.10），并假设色散很小，也可以非常方便地用n和λ表示为

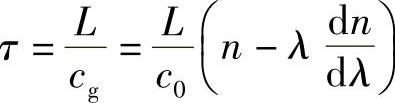
因此

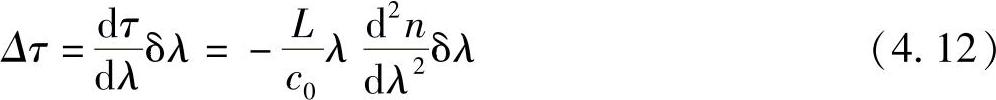
注意到，到达时间的长短取决于d²n/dλ²（或者d²k/dω²），因此取决于光源光谱范围内n和λ（或ω和k）关系的非线性，这种现象称为“群速色散（Group Velocity Dispersion，GVD）”。显然，为使GVD最小化，而使脉冲扩散达到最小，就必须使d²n/dλ²或δλ最小。

在实际应用中可以看到，对于制造光纤的石英材料，发光二极管（光谱宽度约为30nm）在波长850nm时的脉冲扩散约为2.5ns/km，而半导体激光器（光谱宽度约为3nm），脉冲扩展仅约0.25ns/km。满足材料要求的最小GVD（即d²n/dλ²=0）值的条件是在波长1.28nm处，此时，上述各光源的扩散都低一个数量级，所以目前光纤通信系统更喜欢使用的波长为1.28nm。在本书第8和第10章将继续讨论该重要课题。