光传播于均匀电介质中的经典理论

对一束在折射率为n的光学介质中沿Oz方向传播的电磁波，其电场分量的标准表达式为

E=E₀exp[i（ωt-kz）]

已知

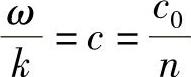
因此，可以写为

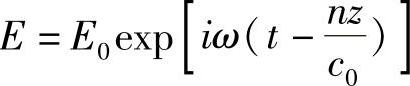
通过定义一个复折射率为

n=n′-in″ （4.1）

从而得到

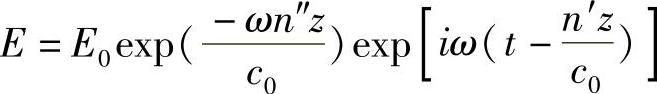
这样可以很方便地使该表达式包括光波的振幅衰减和相位两种特性。显然，第一个指数代表衰减系数（实指数），第二个指数代表正在传播的波（虚指数）。

若电磁辐射通过一种材料介质传播，就会激励原子中的电子振荡，并按基元电偶极子的形式辐射（见附录Ⅴ）。由此产生的辐射的振幅分布，取决于原始波与这些基元电偶极子的散射辐射之间的干涉，因此也可以说它取决于偶极子的分布（见图4.1）。

图4.1　材料介质中的振子激励

正如已知的（见附录Ⅴ），振荡偶极子的辐射图符合余弦二次方定律（朗伯（Lambert）定律）（见图4.1b），最大值垂直于振荡电荷的连线，沿振荡线的辐射为零。显然，在前向传播方向上（与驱动波平行），所有的二次辐射与驱动波都保持固定的相位关系（实际相位差取决于驱动频率与其固有谐振频率间的关系），并且随着沿Oz方向的传播，其相位总是与驱动波的方式相同，所以彼此同相。因此，在前向传播方向上有增强作用，从而形成了强振幅前进波。但它与初级波有不同相位，这是由于初级波与次级波之间有上述的相位差。由此合成波的这个相位变化等效于一个非1的折射率的作用，因为其效应如同对传播速度的改变。事实上，这是材料介质折射率产生的根源。

在某种程度上，由于辐射损耗及原子碰撞，导致二次辐射的基元偶极振子也要衰减，因此初级波也有某些吸收而导致衰减（以及产生散射和介质发热）。用复折射率（complex refractive index）表示这种前向散射过程，就可以同时表示相位变化和损耗。

对于前向之外的其他方向上由散射造成的辐射，其振幅取决于辐射偶极子的分布（即介质中原子或分子的分布）。若散射体规则排列，如晶体，那么只要满足下列条件（见图4.2a），前向之外的其他方向就有最大值：

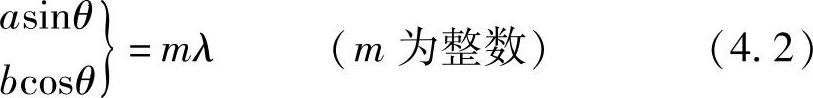
式中，a和b为两个平面间的间隔；θ为相对于前向传播方向的散射角。然而，如果mλ/a>1或者mλ/b<1，由于θ没有实值满足式（4.2），所以就可能没有次级极大值。因此，若λ>a或b，就没有次级极大值，这就是为大多数晶体推导出的条件，除非波长λ远远小于原子间的间隔。这种现象首先出现在X射线波长（<10nm）下，从而形成X射线晶体学学科，并且非常成功地利用X射线探测晶体结构。对于光学波长，除了前向传播方向，晶体中都没有那样的最大值。所以，在纯晶体中，所有光都直线通过而无侧向散射：一束通过纯晶体传播的激光光束，若从与传播方向垂直的方向观察，是无法看到光束的。

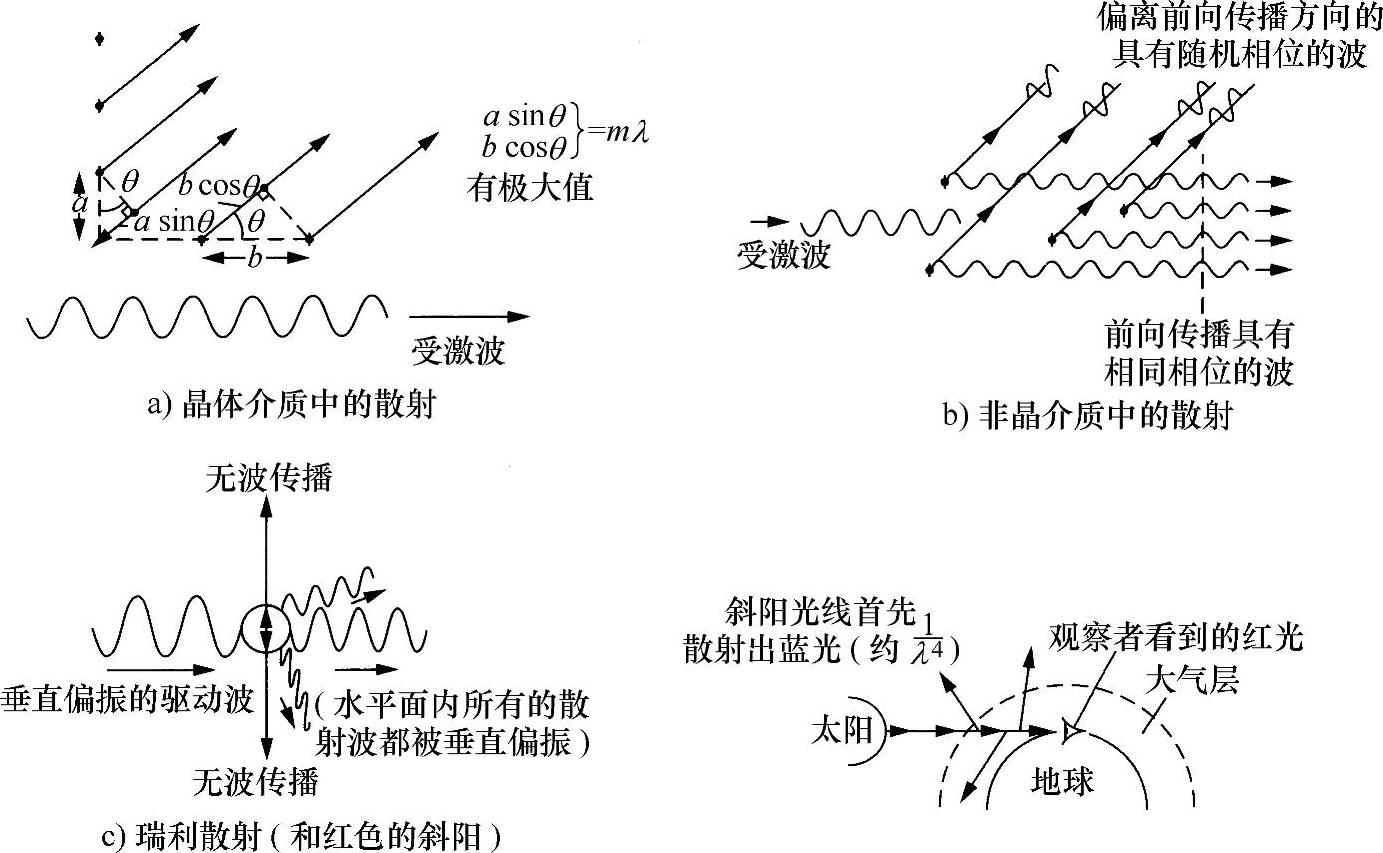
图4.2　光的散射过程

然而，假设散射体随机分布，例如在无定形介质（即非晶体）中，会有什么现象发生呢？尽管在前向传播方向上，由于所有散射体都保持同相，而具有增强效应；但在其他任意方向上，散射波的相位与原子间隔一样，是随机分布的（见图4.2b），所以没有固定的相位关系。（与波长相比，散射体的尺寸必须更小，否则散射体的不同部位会形成相干散射，从而出现最大散射。）随机散射的结果在于（在前向传播方向之外），产生的散射振幅用下列波形的和的形式表示：

∑asin（ωt-kz+δ_i）

式中，δ_i为随机分布的相位。N_T个散射体在该方向形成的光强度由下式给出：

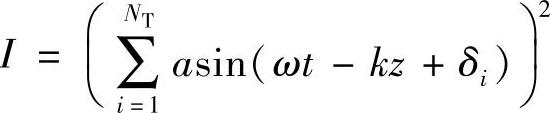
得

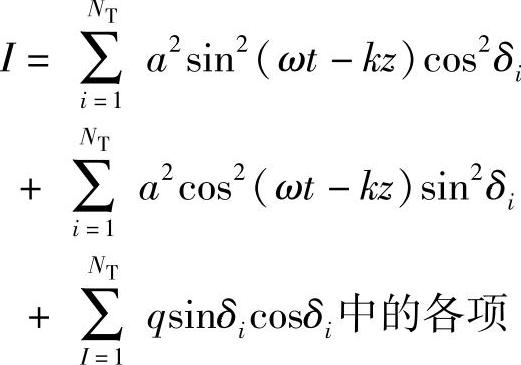
由于δ_i出现正负值的概率相等（若是随机分布），所以在I的表达式中只剩前两项，又因为cos²δ_i和sin²δ_i的平均值是1/2，其结果为

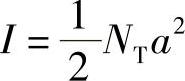
式中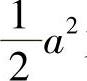，为每个偶极子光强度的均方值。因此，该情况下的光强度恰恰是单个偶极子光强度之和。对于随机散射，该结果直观上讲是正确的。在准备对这些思想进行更为正式的讨论之前，还有一点需要进行如下探讨。

一个振荡偶极子辐射的能量正比于频率的四次方，因此反比于波长的四次方（见附录Ⅴ）。对于无定形介质中的侧向散射体，光强度反比于波长四次方，这是众所周知的瑞利散射性质。最好的例证就是晴朗的蓝色天空。当远离太阳观察时，看到的光是太阳光被大气向侧面散射的光（见图4.2c）。其中，大气由随机排列的分子组成。由于蓝光要比红光的波长小，所以要比红光的散射更有效（约λ⁴），因而天空看起来是蓝色的。同样，太阳本身看起来是红色的（更多的蓝色被散射而远离瞄准线）。在日出和日落时，直射光线必须通过更厚的大气层，甚至显得更红（见图4.2c）。

已经讨论了这些想法的定性“感觉”，下面继续进行定量研究。

已经看到，介质的折射率是由其原子/分子的散射所致。现在推导介质散射源与折射率间的定量关系（记住，在后面章节中，该量是一个复数量），以便考虑速度的变化和衰减。为了能够将上面的理解用于设计和控制，下面就根据基元原子辐射源推导复折射率表达式：

n=n′-in″

应如何进行呢？

首先记住，根据式（2.4），折射率与介电常数有关：

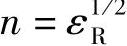
还要知道，ε_R是对介质施加一个电场而产生电偏振（正与负电荷的分离）的结果。事实上，如果单位体积的电偶极矩是P，则根据基础静电学知识得到：

D=ε₀E₀+P=ε_Rε₀E₀ （4.3a）

式中，D为电位移；E₀为施加的场。

也就是说，电荷的这种移动与振荡光学电场一起形成二级辐射，所以，立刻可以完成所需连接，所用方法是将介质的电偏振与电子位移相联系。在此，需要提醒的是，可以利用术语“体积磁化率χ”表示某种介质能够达到这些位移的难易程度。体积磁化率χ定义如下：

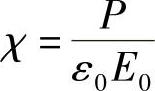
即某给定自由空间位移场产生的单位体积的电偶极矩。

由式（4.3a）会注意到，这就意味着：

ε_R=1+χ （4.3b）

这是静电学中众所周知的关系式。

下面讨论具有下面电场形式的电磁波通过材料传播的情况：

E=E₀exp[i（ωt-kz）]

并假设，与原子间隔相比（即不涉及X或γ射线），该传播辐射的波长（2π/k）足够大。

在场的作用下，介质内原子或分子中的电子将会移动一个量s，该原子中的连接键形成一个“回复力”。相对于原子尺寸，若s是一个中等的量，则该回复力正比于s，并且已经视这种事态描述的是简单谐振运动（Simple Harmonic Motion，SHM）。在SHM中，电子以频率ω_r振荡，即以mω²_rs确定的原子回复力振荡。其中，m为电子质量。此外，由于存在各种耗散力，如振荡电子的辐射、与其他电子/原子碰撞等，都会使振荡衰减。并且，衰减正比于电子的瞬时速度ds/dt，可以用-mγds/dt表示这些损耗。

对于诸如正在研究的被动介质，参数γ总是正值。

使电子产生位移的作用力，是原始波的电场和周围介质的电偏振共同作用的结果。

对于电子位移s，一个基元偶极子的电偶极矩是P=es。其中，e为电子的电荷。若单位体积内有N个偶极子，则介质的电偏振总量为

P=Nes （4.4）(www.xing528.com)

这种局部偏振对其内部一个电荷的作用，等效于位于电荷表面密度等于P的球的球心的一个电荷的作用（可参考任何一本涵盖有静电学基本内容的书，即参考文献[1]）。很容易计算出这种作用等效于大小为P/（3ε₀）的一个场。作用于一个电荷上的总场为

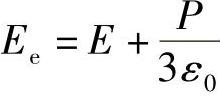
P/（3ε₀）代表周围分子的偏振作用，称为洛伦兹（Lorentz）修正（见参考文献[1]）。

将位移电子看作一个受力的简单谐振子，其运动方程式为

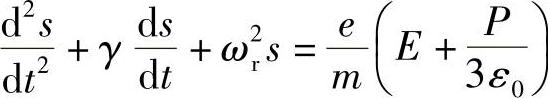
根据式（4.4），替换s后得到

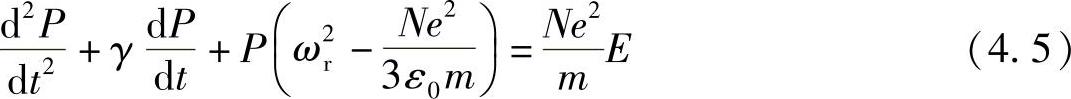
注意，“回复力”项已经修正为

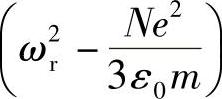
这表明，电子在周围原子间的移动已经将力转换到某给定电子上，也将该电子的固有振荡频率转换成ω_e：

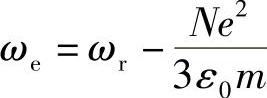
驱动场由下式给出：

E=E₀exp[i（ωt-kz）]

对于式（4.5），可以类似给出下面形式的解：

P=P₀exp[i（ωt-kz）]

若不考虑瞬变态，得到介质偏振度（体积磁化率）的表达式为

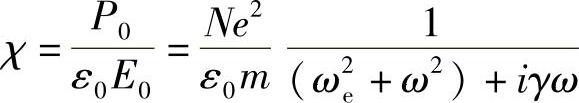
重要的是，ω²_e总是正值，原因在于：如果是负值，电子回复力也是负值，那么原子在电场作用下就应离子化。在这些条件下，不会出现正常的线性传播。

最后，应当得到一个包括具有各种固有振荡频率的电子在内的一般表达式，这才是原子系统的真实情况。总的有效体积磁化率为

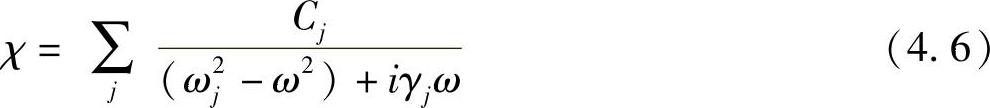
C_j、ω²_j和χ_j都是正值。

注意到

ε_R=1+χ

和

n²=ε_R

因此

n²=1+χ

所以，由式（4.6）得到

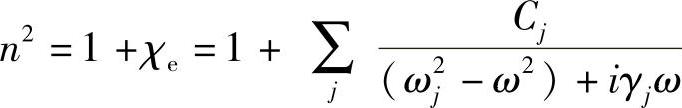
对于低密度介质，如气体，χ_e非常小，利用二项式展开式得

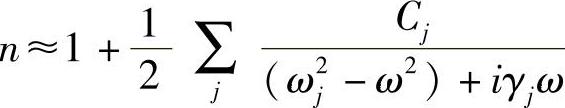
而对于固体介质，该表达式是不成立的，必须应用n的完整表达式。可以利用式（4.1）定义的复折射率确定n，即

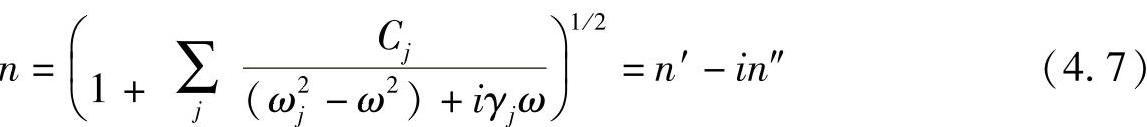
已经注意到，该表达式的虚部（即-in″）就是以指数形式表达损耗项的简单方式。当然，这种损耗是由于γ_j的原因，没有它，n完全就是实数。还注意到，γ_j是由非前向辐射及材料发热而使原子碰撞造成的，碰撞取决于结构动力学，已超出本书的讨论范畴。而辐射损耗也是刚才讨论的那些相互作用过程的结果，也是讨论过了的。

为了确定非前向散射问题，首先要注意，对于电偶极矩振幅为P0的振荡电子，总的辐射能量为（见附录V）：

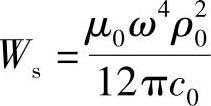
式中，ρ₀为磁导率；c₀为光在自由空间中的速度。如果单位体积内有N个偶极子，则有：

P₀=NP0

式中，P₀为介质的电偏振。根据定义，体积磁化率为

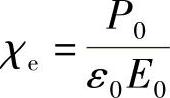
因此

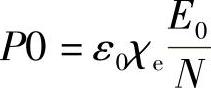
得

其中

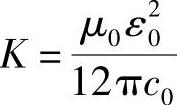
由式（4.6），若ω_j>>ω，并且衰减较小，则W_e与ω近似无关。在该条件下，W_s正比于ω⁴，即正比于1/λ⁴，这就是瑞利散射条件。对于完全消除了分子谐振的那些频率会出现这种情况。如果是谐振情况，散射对频率的依赖更为复杂，散射本身会更强（谐振散射）。

掺杂石英（用于制造光纤）的折射率的实部和虚部随频率的变化如图4.3所示，可以明显看出分子谐振对两种分量的影响。事实上，有可能采用数学方法将实部与虚部联系起来，原因在于，其中每个分量都依赖相同的物理现象（谐振吸收）。相关的数学表达式称为克拉默斯-克朗尼希（Kramers-Kronig）关系式^[2]。若已知一个变量是位于宽频率范围内，原则上可以用该关系式推导出另一个变量。

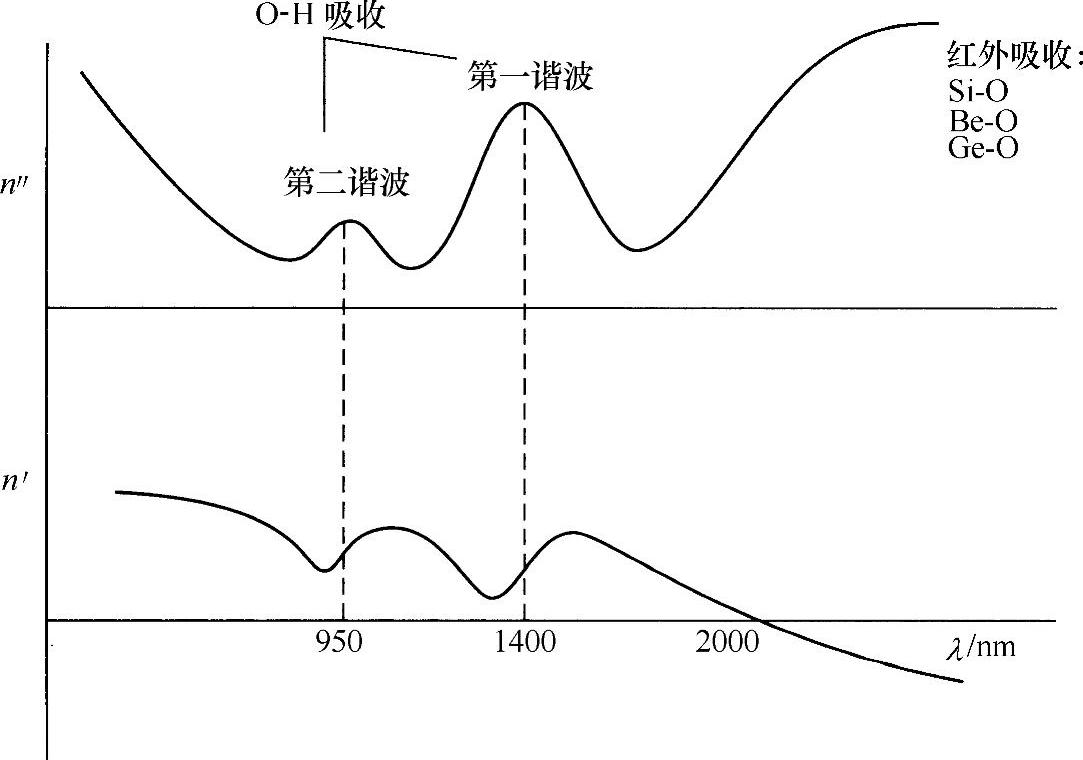
图4.3　掺杂石英的折射率分量