延时器和旋转器在光子学设计中的应用

在3.11节介绍了如何采用庞加莱球来确定一个具有线性双折射和圆双折射的均匀元件与延时器/旋转器对（旋转器在延时器之后）的等效性（见图3.16）。根据上面分析，通过某些矩阵运算定量确定这种等效性是非常简单的。

假设，利用式（3.20）中的矩阵表示均匀元件，并且，（该等效对中的）等效延时器相对于方位q_e延时δ_e，等效旋转器旋转ρ_e。需要求解的矩阵公式为

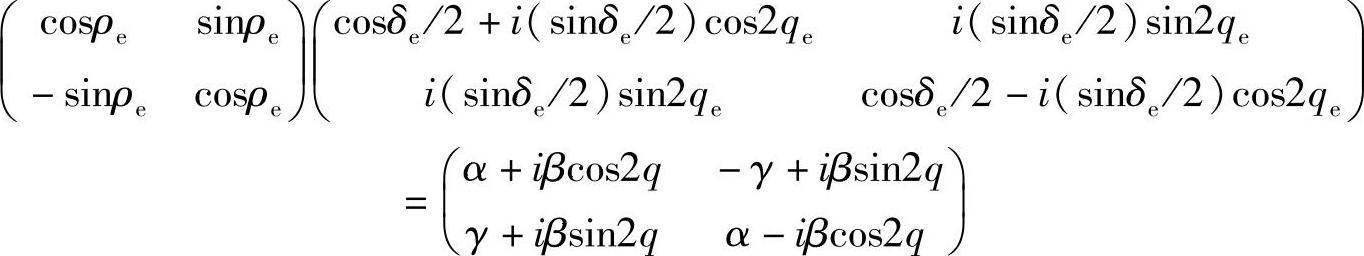
α、β和γ的值与式（3.19）中一样。

这种计算结果（麻烦，但直接明了）为

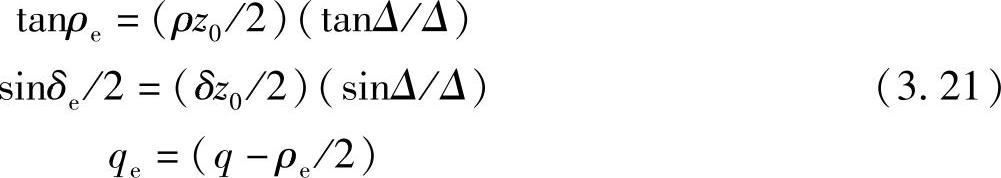
因此，知道了δ、q、ρ和z₀，就可以确定δ_e、q_e和ρ_e，从而定量确定了等效性。

在后续章节（本书第5和第6章）中，一个特别感兴趣的内容是：偏振光两次通过这种均匀元件，首先向前传播，然后向后传播。向前通过该等效线延时器的传播便引入了一个时间延迟，之后等效旋转器旋转。然而，在向后传播时，左手旋转（相对于传播方向）变成了右手旋转，反之亦然。因此，旋转被反转，并被消除（倘若没有磁场作用）。第二次通过延时器使其作用加倍，因为线双折射与传播方向无关。其结果是，仅具有线性双折射和圆双折射的倒易（即没有磁光效应）偏振元件在经光束前后传播后总是显示出一个纯线延时器的性质。

后向传播时，矩阵旋转中含有线性变化量ρ的任何项都会改变符号，前向传播矩阵由下式给出：

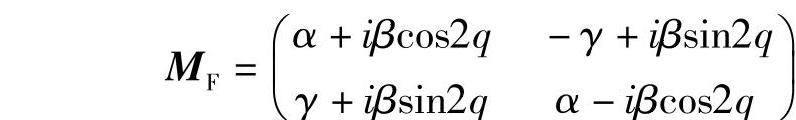
则后向传播矩阵变为(https://www.xing528.com)

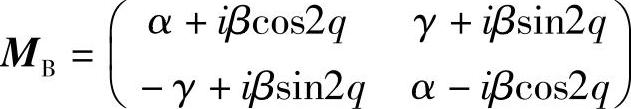
就是说，由于γ=ρz₀（sinΔ/Δ），所以，对于γ，除了改变符号，其他都一样。注意到，Δ=z₀（ρ²+δ²/4）的符号不随ρ改变。

M_B与M_F的非对角线项可以互换。用矩阵术语讲，M_B是M的转置矩阵，写为

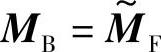
若对传播光进行前向传播运算，就有：

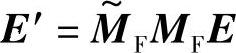
因为m₃/m₄没有实部，所以，计算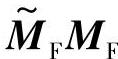，就得到纯延时器的矩阵，即得到下面形式的矩阵：

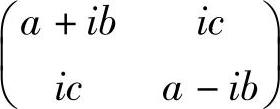
这种运算作为练习留给读者。