琼斯矩阵运算的本质揭示：光子学设计基础第2版成功成果

为了简单起见，在此针对刚才考虑的两种双折射（线性双折射和圆双折射）问题，给出琼斯解的基本内容。作为分析方法，该结论适用于任意一个偏振作用（琼斯考虑了8个，例如包括局部的线吸收和圆吸收）。

定义一组笛卡儿坐标轴OX、OY和OZ，假定有一个元件同时具有均匀分布的线性双折射和圆双折射作用；光束在OZ方向传播的路程为z₀；令线性双折射是每单位长度δ，而圆双折射是每单位长度2ρ。为简化运算，首先假设，OX和OY轴分别与线性双折射的快轴和慢轴重合。

指定所要计算的矩阵（即元件的琼斯偏振矩阵）是M。由下面运算将输入偏振矢量（E_x，E_y）变换为输出矢量（E′_x，E′_y）：

E′=ME

式中，E、E′和M中的分量都是复数。

第一步，根据下式确定新矩阵N：

积分得到

M=exp（Nz） （3.6）

光束在进入元件之前偏振没有变化，设定Z=0处M=I（单位矩阵）就可以确定式中的积分常数。对于所研究的任何矢量，恒等矩阵：

实现着这种保全。

现在，研究厚度为τ的薄片元件。根据式（3.6），该元件的偏振矩阵可以写作下面形式：

M_e=exp（N_eτ） （3.7）

由于N_eτ小，可以将M_e展开为

M_e=1+N_eτ+（N_eτ）/2！+… （3.8）

式中，矩阵公式中的“1”与恒等矩阵有关。

第二步，将薄片元件再分成厚度为τ₁和τ₂的两片（即τ₁+τ₂=τ）。如果与这些新薄片相关的矩阵是M₁和M₂，可以得出结论：

M_e=M₂M₁ （3.9）

（注意，M₁首先作用在该矢量上，所以出现在M₂之后）

由于τ₁、τ₂<τ，可以得出：

M₁=1+N₁τ₁+O（τ²₁）

M₂=1+N₂τ₂+O（τ²₂） （3.10）

式中，O（τ²）代表τ²级或更高次幂的所有后续项。当然，当τ很小时，与Nτ相比，这些项可以忽略不计，所以有：

M_e=M₂M₁=1+N₁τ₁+N₂τ₂+O（τ²） （3.11）

由下式确定一个平均N矩阵：

从而得

整个元件由一系列这种薄板组成，每块矩阵是M_e，因此可以将整个元件的矩阵写成所有这些矩阵的乘积，如下式：

因为在厚度为z₀的元件中，薄板的z₀/τ相同。

由式（3.12），有：

对于连续分布，令τ→0，需要计算：

用二项展开式，并取极限，可以写为

即

所以，由式（3.6），就变成M的N矩阵。

假设，再次讨论分成厚度为τ₁和τ₂的两块薄片，第一块完全是一个延时器，线性双折射是每单位长度δ，其轴平行于OX和OY。若τ很小，由式（3.3）有：

相类似，第二块薄片则是一个旋转器，圆折射率是每单位长度2δ，由式（3.4）有：

由式（3.10）可以看出，当τ→0时的极限值为(www.xing528.com)

和

在这种情况下有：

现在，在不损害一般性的原则下，使两块薄片的厚度相等，即

τ₁=τ₂=τ/2

得

从而，最终实现简化。

知道元件的矩阵，下面就是根据式（3.13）计算矩阵M。自此，公式推导纯粹是一个矩阵代数学的运算过程。

琼斯发现，M与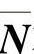本征矢量和本征值之间存在一定关系，并且任何矩阵都可以由其中的一些已知值构成，所以使公式推导又前进了一大步。

一个矩阵的本征矢量，就是在矩阵作用下方向不变、仅数值变化的那些矢量。数值大小变化的倍数就是本征值。对于偏振光学，本征矢量就是在该元件作用下形式没有发生变化的那个偏振态（即一个具有确定椭圆度和方向的椭球）。也就是说，发射椭球和入射椭球有同样形式。

首先，讨论M和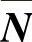一样的本征矢量。若M的两个本征矢量都用E_M表示，则

根据定义有：

ME_M=λ_ME_M （3.15）

式中，λ_M为本征值。使该公式相对于z微分，有：

（当然，E_M与z无关。）

变换式（3.15），发现：

E_M=λ_MM^-1E_M

式中，M^-1为矩阵M的逆矩阵。

代入式（3.16）有：

而

由式（3.5）有：

由于（1/λ_M）（dλ_M/dz）是一个标量，所以式（3.17）就是的本征矢量公式，E_M也是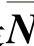N的本征矢量。

此外，由式（3.17），根据下式可以确定的本征值：

或

λ_M=exp（λ_Nz₀） （3.18）

在此，利用z=0时λ_M=1，可以得到积分常数。

现在，利用式（3.14）计算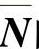的本征矢量和本征值。对于该元件矩阵M，计算本征矢量是一样的，还利用式（3.18）可以计算其本征值。代数运算较直接但冗长，给出下面结果：

式中

其中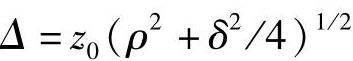

如果线性双折射快轴相对于所选择的轴有一个q角（相对于Y轴），则该矩阵可以归纳为

这是一般公式，适用于只具有线性双折射和圆双折射性的任何均匀元件，其偏振本征矢量代表正交椭球。显然，该方法可以推广到各类偏振光学量，若有K个，就将薄片分割成k个子薄片，则平均后的N为：

或

假设，k个薄片都有相等的厚度。

按照相同方法完成其他计算。显然，根据得到的本征矢量和本征值计算矩阵比较复杂，为此只选择了两个量，以便比较容易地说明该计算方法的原理。