庞加莱球绕直径旋转元件的偏振作用

正如前文所述，由于存在着线性双折射和圆双折射，所以给出的光学元件的偏振特征值（即无需改变偏振形式而传播的状态）是椭圆态的，这些本征值以不同速度传播，因此该元件就呈现出椭圆双折射的性质。

一般地，如果一束椭圆偏振光入射到偏光元件上，一旦出射，就会转换成不同的椭圆偏振态（若输入态本身就是本征态，则是例外）。已经知道，任何椭圆偏振态都可以用两个正交的电场分量（相对于所选择的Ox和Oy轴）表示，即

E_x=e_xcos（ωt-kz+δ_x）

E_y=e_ycos（ωt-kz+δ_y）

或者，用复指数形式表示：

E_x=∣E_x∣exp（iφ_x）　φ_x=ωt-kz+δ_x

E_y=∣E_y∣exp（iφ_y）　φ_y=ωt-kz+δ_y

如果一个无损耗偏振元件的作用，使该椭球转换成另外一个椭球，那么由于是由原始场的方向余弦和旋转产生，所以根据老椭球线性组合分量就会得到新的椭球。新的分量可以写为

E′_x=m₁E_x+m₄E_y

E′_y=m₃E_y+m₂E_y

或者，用矩阵方式表示为

E′=M·E

式中

一般地，m_n为一个复数。M称为“琼斯（Jones）矩阵”，是数学家琼斯为偏振光学的运算发明了特别有用的“琼斯微积分运算”^[2]法而得名的。为了在实践中测量输入和输出态，需要一种快速简便的试验方法。在本书3.4节，曾阐述过人工旋转一个四分之一波片和偏振片的方法，但是现在要介绍的方法则会导致自动运算。

这种方便实用的方法仍然是使用线偏振器和四分之一波片，但该方法是测量这些元件在一系列固定方位上的光强度。

假设，I（θ，ε）表示入射光通过线偏振器后的强度，偏振器与Ox轴的夹角是θ。由于插入了一块四分之一波片，所以使Oy分量延迟一个ε角。其中，波片的轴平行于Ox和Oy。现在，计算下面4个斯托克斯（Stokes）参数：

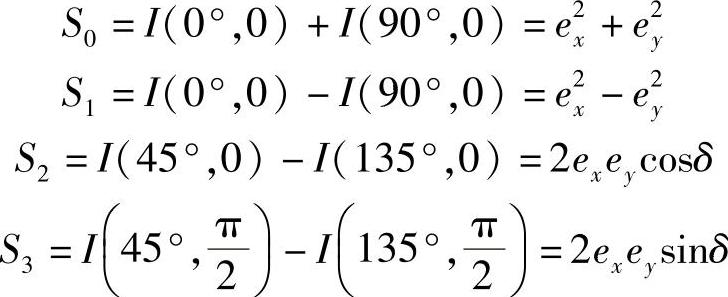
δ=δ_y-δ_x

如果光是100%偏振，由于

S²₀=S²₁+S²₂+S²₃

所以，只有3个参数是独立的。其中，S₀是总光强度。

若光束是部分偏振，则由下式确定偏振度：

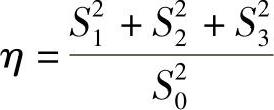
下面，假设光束是全偏振（η=1）。根据下面关系式很容易看出（见附录Ⅳ），S_n的计量代表着偏振椭球的椭圆度e和方位α：

e=tanχ

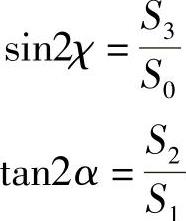
这些关系式为阐述和分析光学偏振现象提供了非常有用的几何方法。斯托克斯参数S₁、S₂和S₃可以看作是一个点对应于Ox₁、Ox₂和Ox₃轴的笛卡儿坐标，因此每种椭圆偏振态都对应着三维空间惟一一个点。由此得出结论：对于常数S₀（无损耗介质），所有这些点都位于半径为S₀的球内——即庞加莱（Poincaré）球内（见图3.19）。该球的性质是众所周知的^[3]。可以看出，赤道圈由连续的线偏振态组成，两极对应着圆偏振的两个相反态。

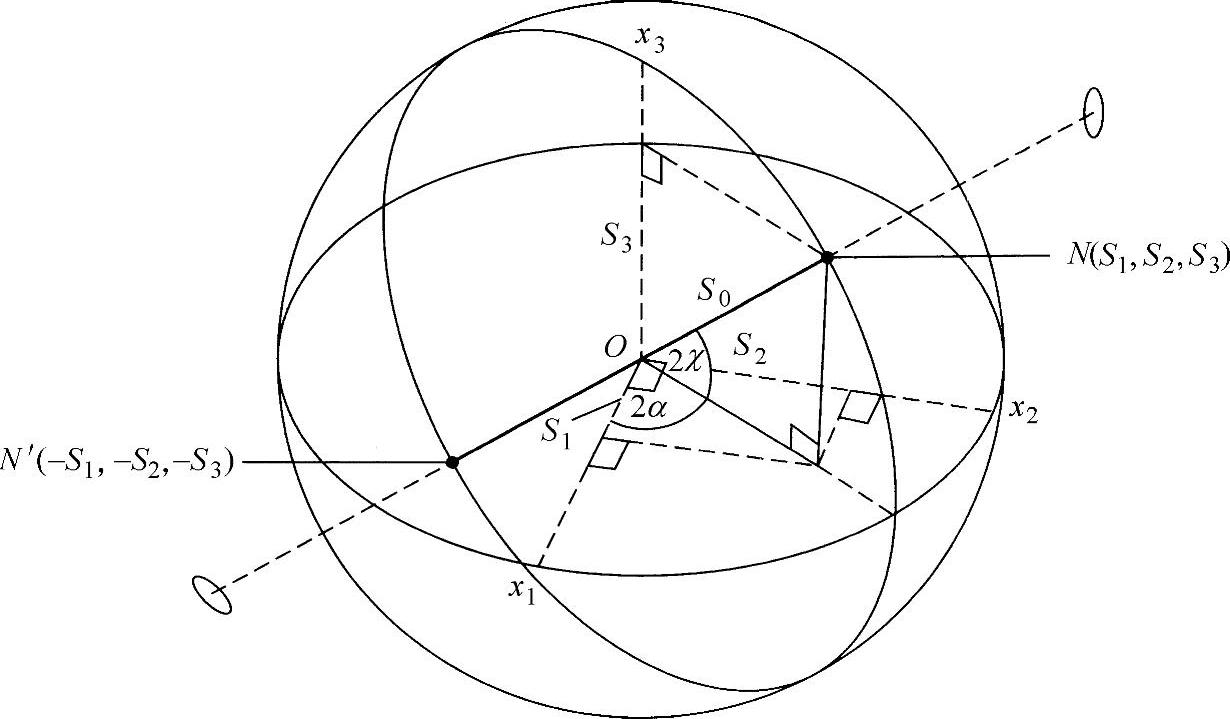
图3.19　庞加莱（Poincaré）球；本征模直径NN′(www.xing528.com)

显然，光束通过无损耗元件产生的任何变化（从一种偏振态到另一种偏振态）都对应着该球绕一条直径的旋转。该球的这类旋转都可以表示为单一的2×2矩阵M。因此，从一种偏振态E到另一种偏振态E′的转换可以表示成下面形式：

E′=ME

或

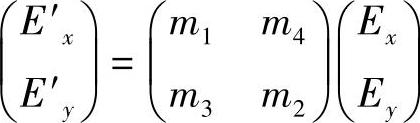
即

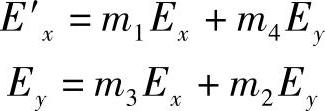
式中

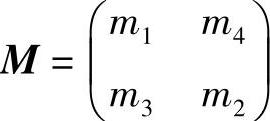
可以将M与前面式（3.2）的M视为一样。

M称为琼斯矩阵^[2]，完全能表示元件的偏振性质，也等效于庞加莱球的旋转。

矩阵的两个本征矢量对应着元件的本征模（或本征态）（即通过元件传播而没有改变形态的那些偏振态）。这两种偏振本征态位于庞加莱球直径NN′两端。元件的偏振效应使该球绕着其直径旋转Δ角（见图3.20），此角度等于本征态之间偏振元件的相位。

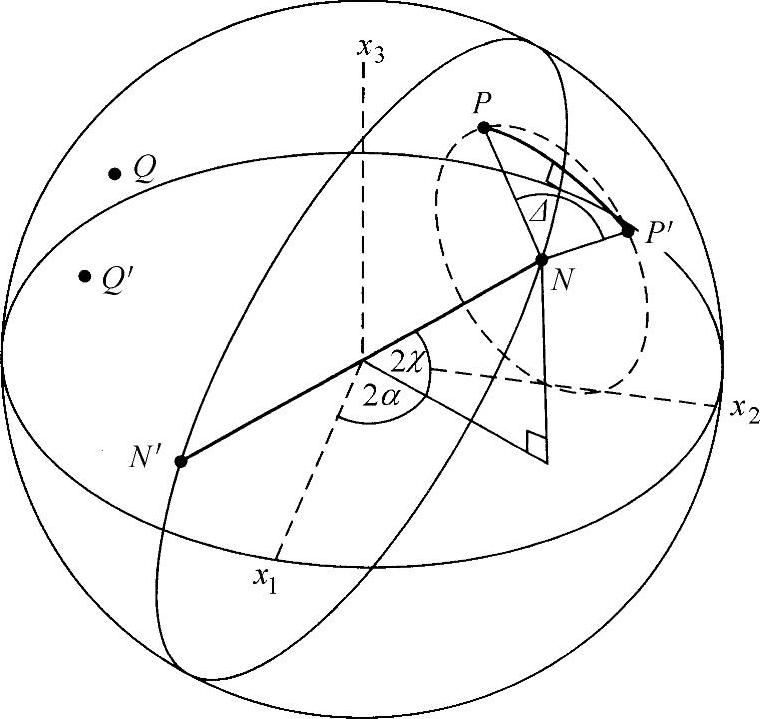
图3.20　庞加莱球绕着本征模直径NN′的旋转

元件的偏振作用，可以看作将输入的偏振态分解为两个具有合适振幅的本征态，并在重新合成为出射态之前于两者之间插入一个相位差。因此，一个纯旋转体（即旋光晶体）等效于两个以反向圆偏振态作为本征态的旋转。这两个本征态间的相速差是圆双折射的度量。相似地，一个单纯的线延时器（如波板）是在正交的线偏振之间插入一个测量线性双折射的相位差，线延时器的本征态位于赤道直径的两端。

在许多应用中，将一个元件的偏振作用分解成线性和圆双折射分量都是非常有用的。庞加莱球清楚地表明，球的旋转总可以分解为两个子旋转：一个绕极直径。另一个绕赤道直径。这种分解总能够完成。

根据上述简短讨论就会慢慢理解庞加莱球的重要性。它将各种偏振态转换为三维空间的可视关系。

为了从图形上得以解释，现在研究一个具体问题。假设一个给定的无损耗偏振元件，事先对其毫不了解，为了完全能确定该元件的偏振性质，试问，必需的最小测量数目是多少？显然，必须提供已知的偏振输入态，并测量出对应的输出态，但是需要多少输入/输出对呢？一个、两个还是更多？

利用庞加莱球很容易回答这个问题。怀疑该元件具有两种偏振本征模，位于某直径两端，需要确定该直径。已经知道，元件的作用等效于该球绕着这条直径以某个角度的旋转，此角度等于安插在本征模之间元件的相位差。如果已知偏振态（NN′）的一个输入/输出对，那么，应该知道，从输入态到输出态的旋转就一定要围绕着一条直径发生，该直径位于垂直且平分两个偏振态连线的平面内（见图3.20）。相类似，其他两个输入/输出态（QQ′）可以确定此类另外一个平面，显然所需要的直径正是这些平面的公共交线。

此外，一旦知道直径，根据任一对偏振态就可以很容易地计算出本征态之间插入的相位差Δ（即该球的旋转角）。

最后的结论是：两对输入/输出态完全可以确定元件的偏振态，简单的几何关系能证明这种结果。一种比较好的方法是利用庞加莱球来确定（显示？）一个问题解的性质，然后，转换成琼斯矩阵以完成精确计算。另外，通常还会遇到一些简单地以球面三角学方式表示的结果。

利用庞加莱球，也可以得到另一个与研究目的直接相关的重要结果，就是具有分布式、重合式、线性和圆双折射的任何均匀元件都等效于两个元件（一个是延时器，另一个是旋转器）的一系列排列，通常这种组合称为延时器/旋转器对（见图3.21）。

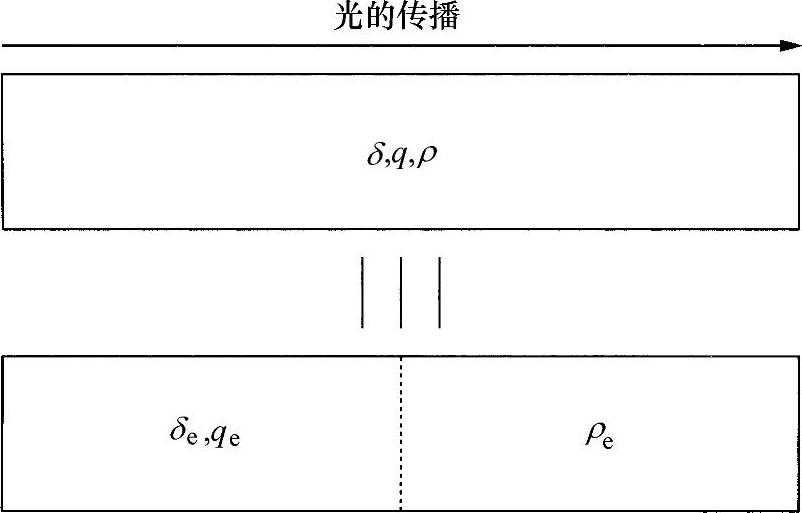
图3.21　延时器/旋转器对的等效性

众所周知，为了确定等效性，令它们是相互正交的椭球，并且对应着庞加莱球直径NN′的两个端点。该元件对任意输入偏振态的作用，例如在P点（见图3.20），将使该球绕直径NN′旋转一个角度Δ，以产生最终的偏振态P′。由庞加莱球的几何图形可以清楚看出，绕赤道直径EE′旋转到A，再绕着极直径OO′（原文错写为00′。——译者注）（见图3.22）从A旋转到P′，也可以实现从P到P′的转换。其中，EE′垂直于包含OO′和P的大圆平面。选择EE′确保第一次旋转位于大圆上，从而使包含P′且垂直于OO′的平面总能相交。

由于E和E′是线形态，所以绕EE′旋转等效于一个延时器；并且，O和O′是两个圆形态，绕OO′旋转相当于一个圆延时器或旋转器。因此，这就等效于提供了一个所需要的延时器/旋转器对。

现在，需要以更详细的数学方法研究琼斯矩阵。

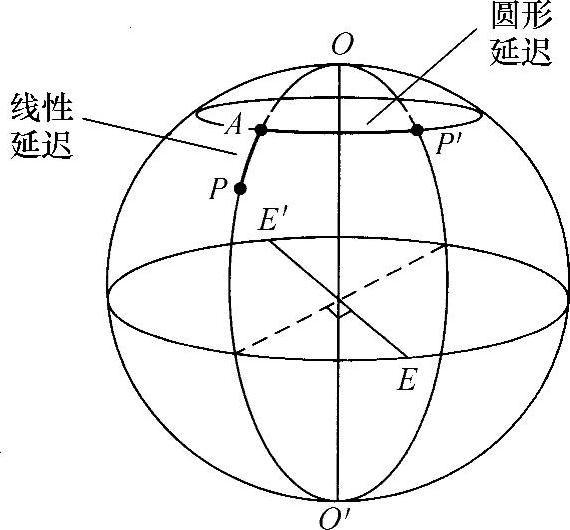
图3.22　延时器/旋转器对的庞加莱球的表示法