减速波片的作用及原理详解

讨论一个正单轴晶体板（石英），采用的切割方式（见图3.7）能使光轴与其中一个端面平行，并假设一束波垂直入射在该端面上。如果该波是线性偏振，其电场E平行于光轴，那么它将以前面叙述过的折射率n_e传播，而与光轴正交的偏振会以折射率n_o传播。

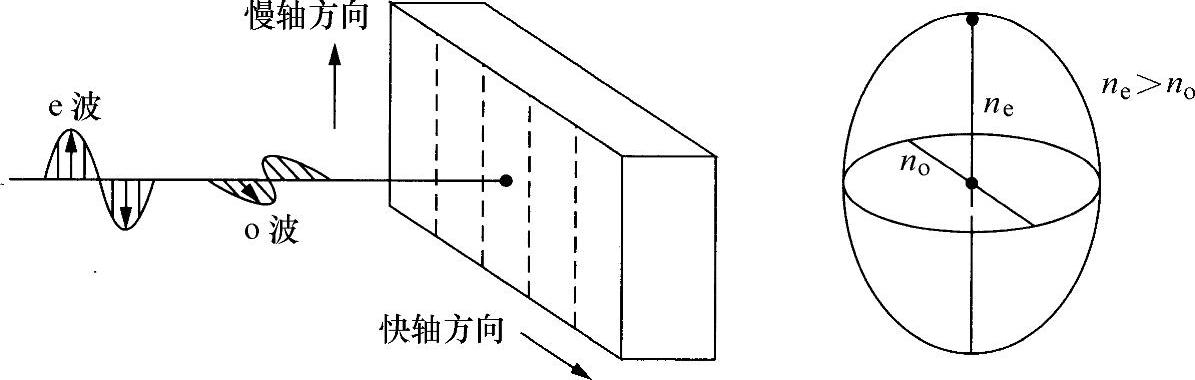
图3.7　端面平行于光轴的石英板

有两束波在相同方向以不同速度通过晶体传播。如果是正单轴晶体n_e>n_o，则平行于光轴的线性偏振光将是一束“慢速”光波，而与光轴垂直的偏振光是“快速”光。为此，常常称两个晶体方向为“慢轴”和“快轴”。

假设，该波在与光轴成45°时是线性偏振。根据下面公式，与光轴平行和垂直的两个分量间的相位差将随进入到晶体内的深度（或距离）而增大，有：

因此，对于给定波长λ，如果：

则

并且，从该晶体板发出的光是圆形偏振光。在两分量之间已经插入了π/2的相位差，等效于λ/4的位移，该厚度的晶体板称为“四分之一波片”。这种波片将（一束以45°角输入偏振方向的）线偏振光转换成圆偏振光，反之亦然。如果输入的线偏振方向与光轴成α的任意夹角，则两个分量为

Ecosα

Esinα(www.xing528.com)

有π/2的相位差。在本章3.2节我们注意到，沿偏振椭圆两个轴方向的电场分量总是存在90°的相位差，由此得出结论：这两个分量是该晶体板椭球偏振态的长轴和短轴。椭圆的椭圆度（即长轴与短轴之比）恰好就是tanα。通过改变输入的偏振方向α，就可以得到能够产生具有任意椭圆度椭圆的方法。椭圆的方位取决于波片光轴的方向（见图3.8a）。

图3.8　利用波板控制偏振

假设，晶片的厚度是前面给出厚度的两倍，并使用同样波长，就变成了一块“半波片”，分量（线性本征态）之间就插入了相位差π。其结果是，与光轴成α角的线性偏振输入光仍然是线性偏振光，但偏振方向与光轴成-α夹角。该晶片使偏振方向旋转了-2α。的确，任意的输入偏振椭圆将以相同的椭圆度出射，但方位旋转了-2α（见图3.8b）。

通过上述两个简单晶片可以得出结论：由线性偏振光可以形成具有任意椭圆度和方向的椭圆偏振，其中线性偏振光本身可以由任意光源和简单的偏振片形成。

相反过程有同样价值，即分析具有任意椭圆形的偏振态，或者反转到线性态。

假设，有一束未知的椭圆偏振光。安插一块偏振片，并使之绕着一根平行于传播轴方向的轴旋转（见图3.9）。这样就会找到具有最大透射率的位置和最小透射率的正交位置，分别是椭圆的长轴和短轴。两位置处两个光强度之比是该椭圆椭圆度的二次方，即

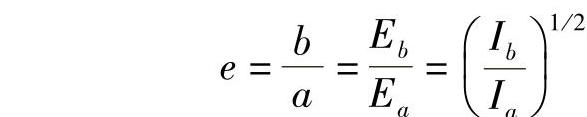
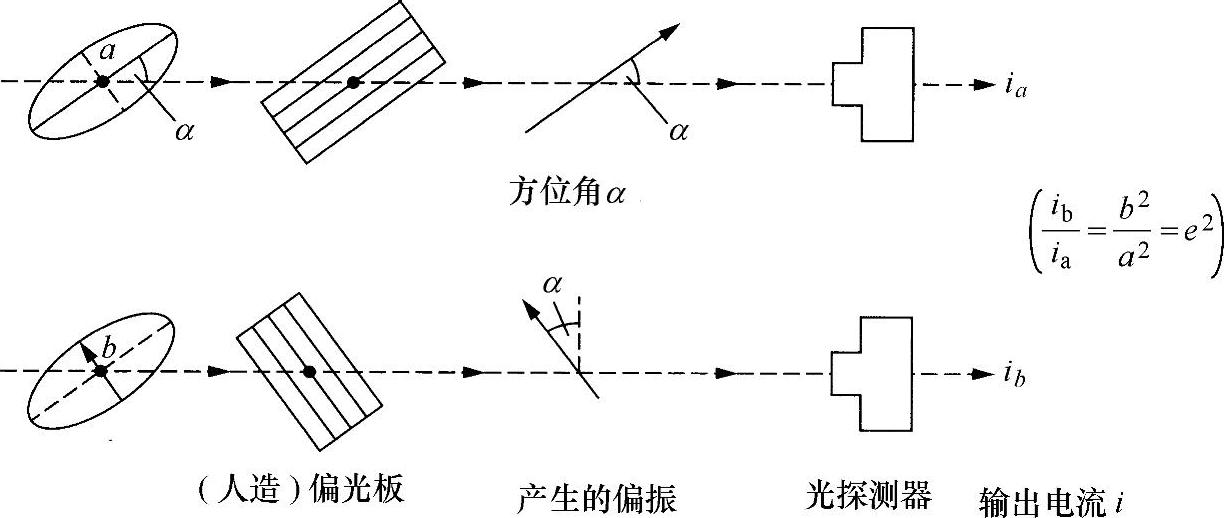
图3.9　偏振椭圆的确定

显然，根据定义，椭圆的方位恰恰是长轴方向，并可以根据最大值出现的位置确定。为了将椭圆态转换成线性态，需要的就是一块四分之一波片（要与使用的光波波长相匹配）。由于沿椭圆长轴和短轴方向的电场分量总是有90°的相位差（见3.2节），所以，插入一块四分之一波片，并使其轴与偏振椭圆的轴对齐，就会使分量同相或反相，光就成为线性偏振。将四分之一波片与一块紧随其后的偏振片（或者棱镜偏振器）组合在一起，并且使两者（单独地）绕着传播轴旋转，直至没有光出现，要求四分之一波片的方位必须与椭圆的轴对准。这是因为只有当光变成线性偏振光时，偏振器才能完全使其消失（如果不存在使光消失的位置，表明光没有完全得到偏振）。

这些都是利用非常简单的装置就能完成的很有用的操作和分析方法。然而，通过旋转偏振板进行人工干涉并不总是很方便的或有可行性的。在许多情况下，必须利用电子处理技术非常迅速（或许在纳秒数量级）和自动地完成偏振分析和控制。为此，要采用更为先进的偏振装置，并且为了理解和应用这些装置，需要有更为先进的理论支持。这些在3.8节将进一步进行介绍。