晶体光学：晶体的光学响应、双轴晶体和单轴晶体

激励基本的原子偶极子振荡而产生辐射，从而使光通过一种材料进行传播。在前面的讨论中，假设受力振荡发生在驱动电场的方向，但是若一种介质的物理性质随方向变化，即各向异性介质，就不是这种情况。如果原子或者分子中的电子在一个方向的移动要比另一方向更为容易，那么与最佳方向成任意角度下的电场将使该电子在与该场不平行的方向上运动（见图3.3）。因此，振荡偶极子具有最大辐射的方向（与振荡方向垂直的方向）与驱动波的方向并不相同。

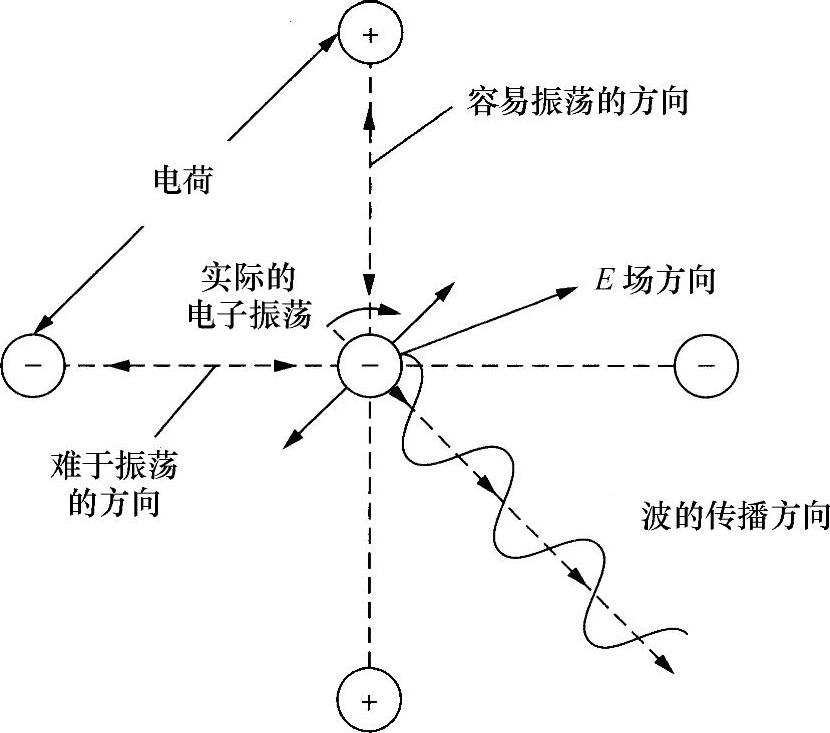
图3.3　各向异性介质中电子对电场的响应

对于各向异性介质的光学元件，即使是单片结构件也没有那么简单。

很明显，若是各向同性介质（没有方向性），前面已经讨论过，其电位移D与电场E之间的关系为

D=ε_Rε_oE

若是各向异性介质，会比较复杂。事实上，其关系式必须是下面形式（对于任意的三个正交方向Ox、Oy和Oz）：

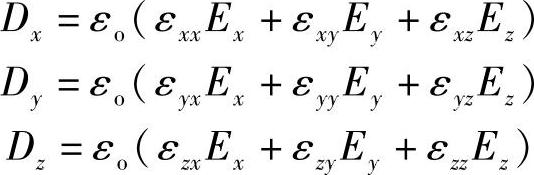
显然，在此讨论的内容是一个阐述晶体内各个方向具有不同电场磁化率的矩阵：ε_ij（一个标量）是第j个方向上的电场在晶体内第i个方向所产生效应的一种度量（就是说，在该方向上可以使电子移动，从而形成一个偶极矩的容易程度）。

可以将该矩阵表示成简单形式：

D_i=ε_oε_ijE_j（i，j=x，y，z）

现在，ε_ij为众所周知的张量，在这种情况中称为介电常数张量。张量是采用矩阵表达形式表述各向异性介质某特定物理性质的一个物理量。显然，现在，D不再（一般来说）与E平行，两个量之间的夹角取决于材料中E的方向。

从能量方面考虑（见附录Ⅲ）可以看出，电容率张量是对称的（即ε_ij=ε_ji）。如果用一组由晶体结构^[1]确定的特定轴（主轴）表示对称张量，则对称张量就可以表示成对角线形式。如此就有：

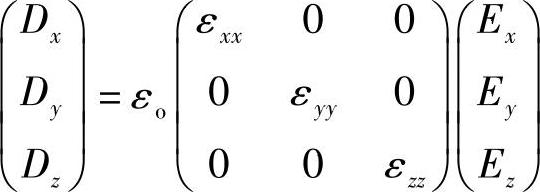
现在，新轴系Ox、Oy和Oz就是这种特定的轴系。

假设，E=E_xi，这就意味着，插入该晶体，就会产生一个电场E位于晶体某个特定方向上的光波。

在这种情况中，有下面较简单的形式作为张量关系式，并且e_xx是一个标量：

D_x=ε_oε_xxE_x

换句话说，就与各向同性材料一样，D平行于E，光束完全以正常方式在折射率等于e^1/2_xx的材料中传播。此外，对于下面情况，也是正确的：

E=E_yj（折射率为e^1/2_yy），

E=E_zk　（折射率为e^1/2_zz）

在继续讨论之前，应当注意上面推导过程中的一个重要结果：折射率随E的方向而变化。当一束波沿Oz方向传播，其速度将取决于其偏振状态：若该波在Ox方向是线性偏振，其速度是c₀/e^1/2_xx；若该波在Oy方向是线性偏振，其速度是c₀/e^1/2_yy。因此，该介质为上述方向上传播的波提供两种折射率，这种现象称为“双折射”。对于在与Ox轴成45°方向上的线性偏振波，它将分成两个相等的分量，即Ox和Oy方向形成线性偏振，但以不同速度传播。两个分量之间的相位差将稳定地增大，波的合成偏振态将逐渐从线性变化到圆，再返回到线性。(www.xing528.com)

当然，这种特性是早期讨论的基本物理学的一个结果。在各向异性晶体中，电场使原子中的电子在一个方向移动要比其他方向更为容易些，因而，对于比较容易移动的方向，偏振光可能比移动较迟缓的方向传播更快些。论述双折射，并非几句话的事，但依赖的物理原理非常简单。由这些讨论可以得出以下结论：借助于与Ox、Oy和Oz轴偏振方向相对应的三个折射率，值分别是e^1/2_xx、e^1/2_yy和e^1/2_zz，可以表示出各向异性介质的性质。利用这些知识也可以确定一个方向上的波在某给定线偏振态下的折射率（因此也确定了速度）。

为此，根据某给定晶体的电容率张量形式设计了一个“折射率椭球”（见图3.4）。这种椭球具有下述重要性质。假设，我们希望讨论的是与晶轴成任意角度传播的光（至今没有规定偏振）。那么，画一条线OP，与折射率椭球内过中心O的方向相对应（见图3.4）。现在，画一个平面，也通过点O，并与上述直线垂直。该平面与椭球相切，形成一个椭圆。该椭圆具有下面性质：其长轴和短轴方向确定了D和E是平行的线偏振传播方向，并且，轴OA和OB的长度等于这些偏振的折射率。由于这两种线性偏振态在该晶体方向是惟一无须改变偏振形式而传播的偏振，有时又称为该方向的“本征态”或“偏振本征模”，符合本征矢量和本征值的矩阵术语称呼。

首先考虑的传播方向Oz对应着椭球的一个轴，两种折射率e^1/2_xx和e^1/2_yy是垂直于Oz轴的中心平面内其他两个轴的长度。

折射率e^1/2_xx、e^1/2_yy和e^1/2_zz称为主折射率，此后将表示为n_x、n_y和n_z。

还有另外几点值得注意。首先，假设：

n_x>n_y<n_z

由此可以得出结论：包含Oz在内的一个平面，其与椭球相交的两个轴相等（见图3.5）；该平面与yz面成一夹角，因此与椭球成一个圆。这就意味着，对于与该平面法线对应的光传播方向，所有的偏振方向有相同的速度，该方向没有双折射。该方向就是晶体的光。一般来说，由于在另一侧一定也有这样一个平面，与yz平面形成相等角度（见图3.5），所以会有两个这样的轴。具有两个光轴的此类晶体称为双轴晶体。

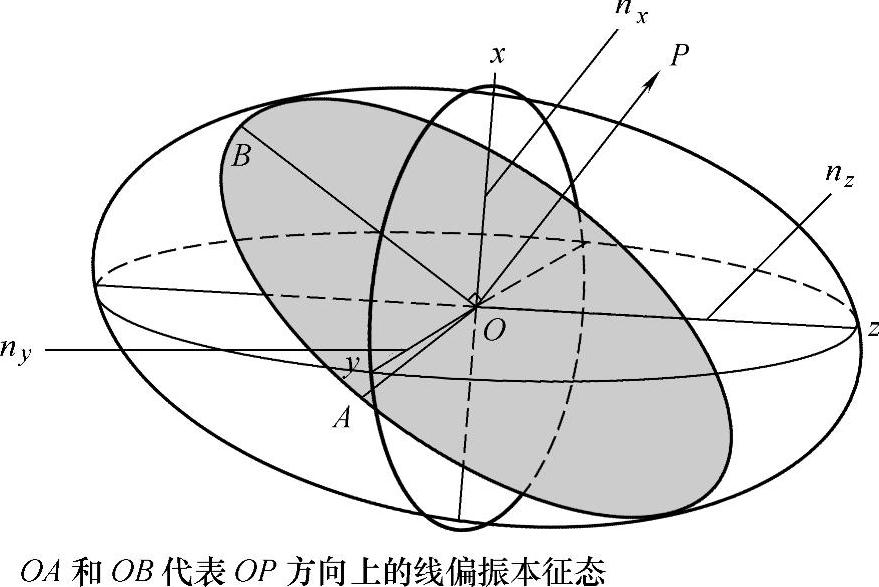
图3.4　折射率椭球

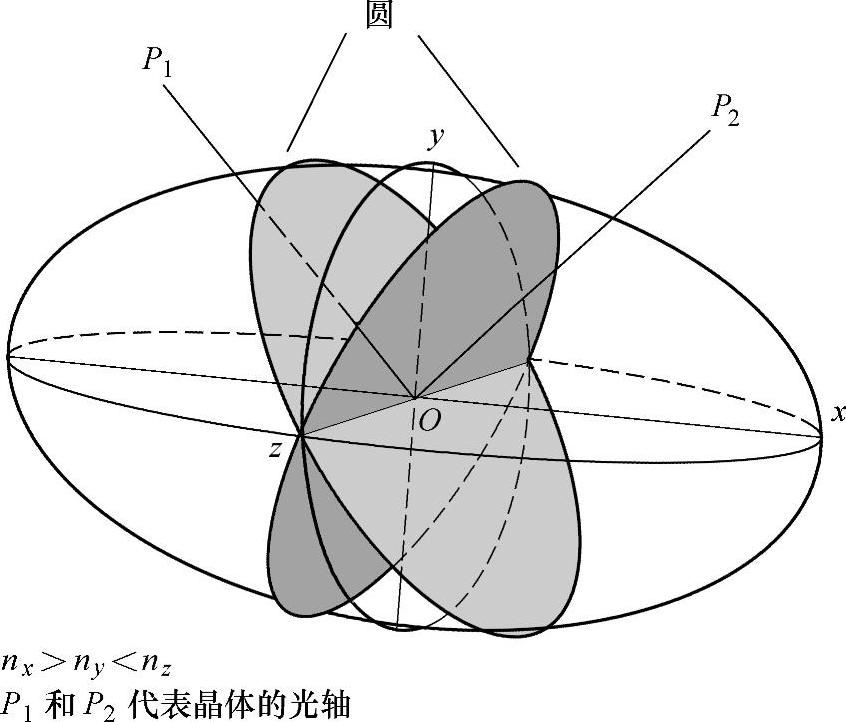
图3.5　双轴晶体的椭球

那么，假设：

n_x=n_y=n_o（假设n_o为“寻常”（ordinary）折射率）

和

n_z=n_e　（假设n_e为“非常”（extraordinary）折射率）

在这种情况下，其中一个主平面是圆，并且是惟一存在的圆形截面（包含原点），因此只有一个光轴沿Oz方向，这种晶体称为单轴晶体（见图3.6）。n_e>n_o时，这种晶体是正晶体；n_e<n_o时，是负晶体。例如，石英是一种正单轴晶体，方解石是负单轴晶体。当然，这些性质还取决于这些材料的晶体类别。

显然，折射率椭球是一种确定各向异性介质偏振性质非常有用的工具。

下面就讨论所有上述性质中一些较实用的结果。

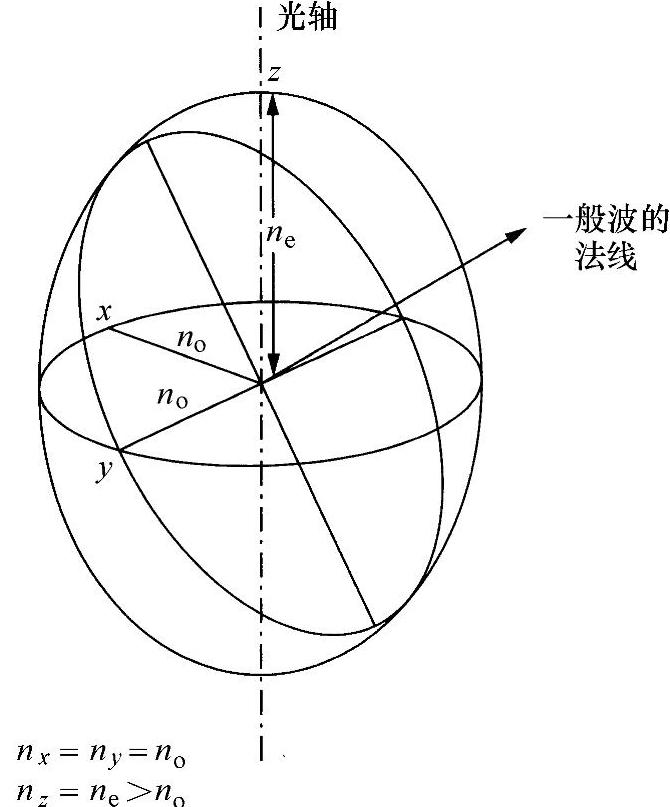
图3.6　一种（正）单轴晶体的折射率椭球