光子学设计基础：偏振椭球及形式表达式

在本书2.4.1节，根据Ox和Oy方向上的两个线性偏振分量推导出偏振光波沿Oz方向传播的最一般形式（见图3.1）：

E_x=e_xcos（ωt-kz+δ_x）

E_y=e_ycos（ωt-kz+δ_y） （3.1a）

从上述方程中消除（ωt-kz），得到如下表达式：

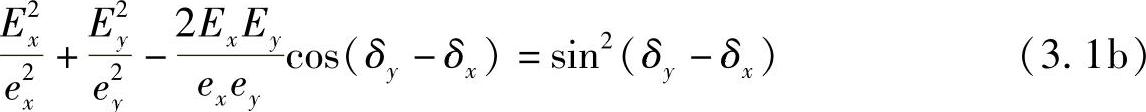
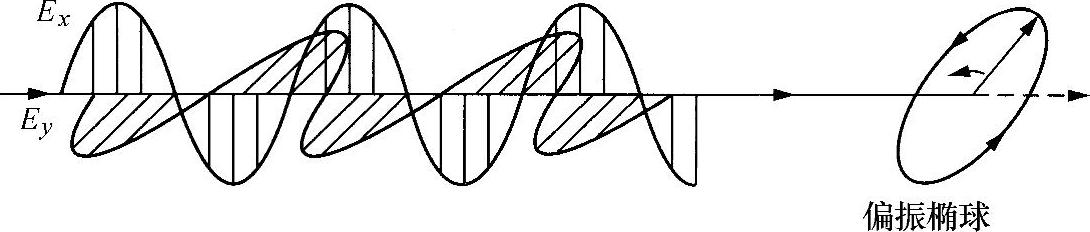
图3.1　一个椭圆偏振波的分量

这是合成电矢量端部在合成波一个周期内在空间任一点环绕成的椭圆（变量是E_x，E_y）。然而，只有在相位差（δ_y-δ_x）一直保持常数，或者至少在与探测器的响应速度相比只是缓慢变化的情况下，该公式才是正确的。换句话说，两束波必须具备大的“相干性”，否则，相对相位和合成的场矢量在探测器的响应时间内会随机变化，合成场不会呈现出有序图形，因而传播给探测器的基本上是非偏振光。

假设，相干性非常好，下面将进一步研究椭圆偏振的性质。

首先注意到，椭圆总是位于图3.2所示的矩形框中，但是椭圆的轴并不平行于原始坐标系的x、y方向。

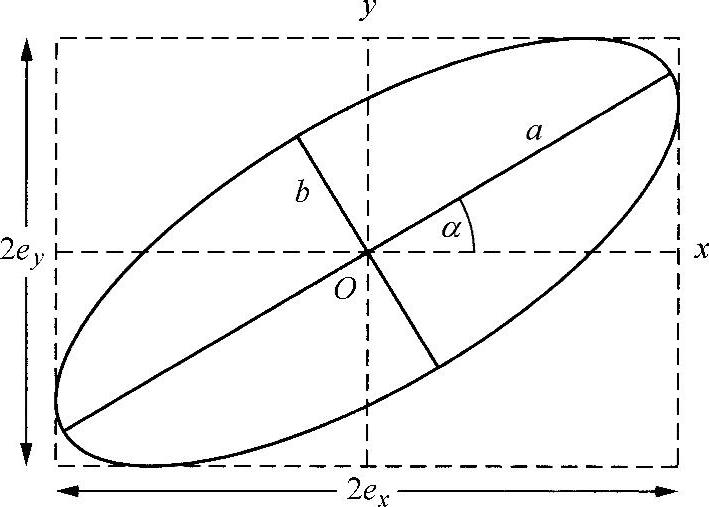
图3.2　偏振椭圆

对椭圆的具体规定如下：已知e_x，e_y，δ（=δ_y-δ_x），假定tanβ=e_y/e_x。

椭圆的方位α由下式给出（见附录Ⅳ）：

tan2α=tan2βcosδ

半长轴和半短轴a和b为

e²_x+e²_y=a₂+b²～I

椭圆率e为

e=tanχ=±b/a　（符号决定旋转方向）(www.xing528.com)

式中

sin2χ=-sin2βsinδ

还应当注意，沿长轴和短轴方向的电场分量总是正交的（即π/2相位差，其符号取决于旋转方向）。

线偏振态和圆偏振态可以认为是偏振椭圆分别蜕化为直线或圆的特殊情况。

若下面条件得到成立，利用式（3.1a）的分量表达式就可以得到一种线形态：

或者

δ_y-δ_x=mπ

式中，m为整数。若是后面一种情况，偏振方向相对于Ox轴的角度为

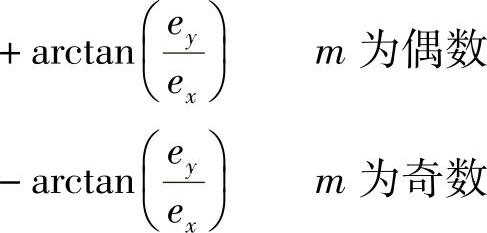
满足下列条件时，得到圆偏振态为

e_x=e_y

和

（δ_y-δ_x）=（2m+1）π/2

就是说，在这种情况下，两种波有相等的振幅和相位正交。m为偶数时，该波是右旋圆偏振态；m为奇数时，为左旋圆偏振态。

物质固有的方向性可以使光成为偏振光：或者物质本身就是偏振光源，或者使光通过该物质。材料固有的这种方向性，是由于在键和过程中材料内的原子结合在一起而具有的。这种方向性可以使材料根据不同类型的作用力（如电、磁或者机械力）的方向而改变响应。通过研究晶体材料可以对固体材料中的方向性有非常清晰的了解。有各种各样的结晶形式，一些是对称的，一些是不对称的。某些有代表性的晶体形状是源自下面事实：这些晶体沿着某些平面（即解理面（cleavage plane），这些平面之间的原子力最弱）较容易断裂。

对于晶体材料，一般地，是在产生光的过程中，或者光通过晶体材料施加偏振效应于其上时，产生方向性。

为了解产生、控制和应用偏振光的方法，就必须逐渐了解晶体光学方面的内容。